§ 28. Gravity and the force of universal gravitation
Chapter 3. Forces in mechanics- Why does the Moon move around the Earth?
What happens if the moon stops?
Why do planets revolve around the Sun?
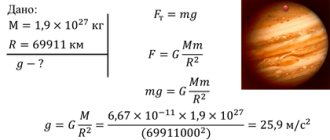
Chapter 1 discussed in detail that the globe imparts to all bodies near the surface of the Earth the same acceleration - the acceleration of gravity. But if the globe imparts acceleration to a body, then, according to Newton’s second law, it acts on the body with some force. The force with which the Earth acts on a body is called gravity
. First we will find this force, and then we will consider the force of universal gravity.
Acceleration in absolute value is determined from Newton's second law:
In general, it depends on the force acting on the body and its mass. Since the acceleration of gravity does not depend on mass, it is clear that the force of gravity must be proportional to mass:
= m (3.1)
The physical quantity is the acceleration of gravity, it is constant for all bodies.
Based on the formula F = mg, you can specify a simple and practically convenient method for measuring the mass of bodies by comparing the mass of a given body with a standard unit of mass. The ratio of the masses of two bodies is equal to the ratio of the forces of gravity acting on the bodies:
It means that
| It is important that the masses of bodies are the same if the forces of gravity acting on them are the same. |
This is the basis for determining masses by weighing on spring or lever scales. By ensuring that the force of pressure of a body on a pan of scales, equal to the force of gravity applied to the body, is balanced by the force of pressure of weights on another pan of scales, equal to the force of gravity applied to the weights, we thereby determine the mass of the body.
| The force of gravity acting on a given body near the Earth can be considered constant only at a certain latitude near the Earth's surface. If the body is lifted or moved to a place with a different latitude, then the acceleration of gravity, and therefore the force of gravity, will change. |
The force of universal gravity. Newton was the first to strictly prove that the cause of a stone falling to the Earth, the movement of the Moon around the Earth and the planets around the Sun are the same. This is the force of universal gravity
, acting between any bodies in the Universe.
Newton came to the conclusion that if it were not for air resistance, then the trajectory of a stone thrown from a high mountain (Fig. 3.1) at a certain speed could become such that it would never reach the surface of the Earth at all, but would move around it like the way the planets describe their orbits in celestial space.
So, according to Newton, the movement of the Moon around the Earth or the movement of the planets around the Sun is also a free fall, which lasts, without stopping, for billions of years. The reason for such a fall (whether we are really talking about the fall of an ordinary stone to the Earth or the movement of planets in their orbits) is the force of gravity.
The Earth imparts an acceleration to the Moon, which does not depend on the mass of the Moon and, as calculations have shown, is (60)2 times less than the acceleration of bodies on Earth. The distance to the Moon is 60 times the radius of the Earth. From here Newton concluded that the acceleration and, accordingly, the force of attraction of bodies to the Earth are inversely proportional to the square of the distance to the center of the Earth:
Newton also established that the Sun imparts to all planets an acceleration inversely proportional to the square of the distance from the planets to the Sun.
The law of universal gravitation. One can only guess about the excitement that gripped Newton when he came to the great result: the same cause causes phenomena of an amazingly wide range - from the fall of a thrown stone to the ground to the movement of huge cosmic bodies.
Newton found this reason and was able to accurately express it in the form of one formula - the law of universal gravitation.
Since the force of universal gravitation imparts the same acceleration to all bodies regardless of their mass, it must be proportional to the mass of the body on which it acts:
| “Gravity exists for all bodies in general and is proportional to the mass of each of them... all planets gravitate towards each other...” I. Newton |
But since, for example, the Earth acts on the Moon with a force proportional to the mass of the Moon, then the Moon, according to Newton’s third law, must act on the Earth with the same force. Moreover, this force must be proportional to the mass of the Earth. If the force of gravity is truly universal, then from the side of a given body a force must act on any other body proportional to the mass of this other body. Consequently, the force of universal gravity must be proportional to the product of the masses of interacting bodies. of the law of universal gravitation comes from:
.
| Law of Universal Gravitation The force of mutual attraction between two bodies is directly proportional to the product of the masses of these bodies and inversely proportional to the square of the distance between them: |
| Remember The proportionality coefficient G is called the gravitational constant . |
The gravitational constant is numerically equal to the force of attraction between two material points weighing 1 kg each, if the distance between them is 1 m. Indeed, with masses m1 = m2 = 1 kg and distance r = 1 m, we obtain G = F (numerically).
It must be borne in mind that the law of universal gravitation (3.4) as a universal law is valid for material points. In this case, the forces of gravitational interaction are directed along the line connecting these points (Fig. 3.2, a).
It can be shown that homogeneous bodies shaped like a ball (even if they cannot be considered material points, Fig. 3.2, b) also interact with the force determined by formula (3.4). In this case, r is the distance between the centers of the balls. The forces of mutual attraction lie on a straight line passing through the centers of the balls. Such forces are called central
. The bodies that we usually consider falling to Earth have dimensions much smaller than the Earth's radius (R ≈ 6400 km).
Such bodies can, regardless of their shape, be considered as material points and determine the force of their attraction to the Earth using the law (3.4), keeping in mind that r is the distance from a given body to the center of the Earth.
| A stone thrown to the Earth will deviate under the influence of gravity from a straight path and, having described a curved trajectory, will finally fall to the Earth. If you throw it at a higher speed, it will fall further." I. Newton |
Determination of the gravitational constant. Now let's find out how to find the gravitational constant. First of all, note that G has a specific name. This is due to the fact that the units (and, accordingly, the names) of all quantities included in the law of universal gravitation have already been established earlier. The law of gravitation gives a new connection between known quantities with certain names of units. That is why the coefficient turns out to be a named quantity. Using the formula of the law of universal gravitation, it is easy to find the name of the unit of gravitational constant in SI: N • m2/kg2 = m3/(kg • s2).
End of paragraph >>>
Lesson on the topic "Mechanical work. Power."
Topic: Mechanical work. Power.
Lesson Objectives
:
Educational
: repeat and consolidate acquired knowledge on the topic “Mechanical work. Introduce the concept of “power”.
Developmental
: develop logical thinking, skills in solving qualitative, computational and practical problems, the ability to work with various types of tasks, broaden the horizons of students.
Educational
: to cultivate interest in studying physics, developing skills in collective and group activities.
Lesson type
: lesson in the formation of skills and abilities.
Call stage
1. Organizational stage:
In the last lesson we studied the concept of mechanical work. In today's lesson, we need to repeat and consolidate the knowledge gained on this topic and get acquainted with another physical quantity that is closely related to mechanical work. Let's start the lesson by reviewing definitions.
(Work with a cluster prepared by students at home. (flow chart that reflects key concepts related to work: designation, units of measurement, formula, work is positive, negative, equal to zero.)
2. Brainstorm
:(slides 1-3)
Collective updating of knowledge
:
Questions:
— What is the everyday meaning of the quote? What is its physical meaning? Divide the pictures into two groups. Explain this choice. (Mechanical and non-mechanical work).
— Do the heroes of the fairy tale “Turnip” do their work?
- What forces do the work? Identify the work sign.
3.
Experiment:
Two students do the work of lifting a weight.
Students time their work. Conclusion
: operating time varies. Therefore, the power of work is different.
For many engineering and technical tasks, it is not only the work being performed that is important, but also the speed at which the work is completed. After all, the same work can be done at different speeds: for example, a load can be lifted slowly or quickly. The speed of work is characterized by power. So, the new quantity we are getting acquainted with today is “Power.” (slide 4-5)
Conception stage:
1.) Power characteristics:
— A physical quantity that characterizes the speed of work is called power.
— Scalar, because has no direction. [ N] = W . The name of this unit of power is given in honor of the English inventor of the steam engine (1784), James Watt. 1 W = power at which 1 J of work is done in 1 s.
2.) Practical task:
Calculate the power developed by students when performing exercises.
3)Reading a poem: (slide 6)
The horse was restive and well-fed. And become and trot like an expert. When he hit the ground with his hoof, the earth springs slightly. His eyes were wild, his running was elastic, he was trotting as if he were swimming. And if he neighed, the backs of mares trembled all over the area...
Questions:
— Do you think a horse has anything to do with physics?
— What physical quantity is a horse associated with? (1 hp = 735 W; 1 hp is the average work in 1 s that a strong draft horse could do, working evenly all day long.)
Question: Which car will you choose? Give reasons for your choice. (slide 7)
What determines the speed of movement of such bodies? It turns out that it directly depends on the power of the car engine.
On the students' desks are the technical passports of the cars. Determine engine power. Indeed, the engine power of cars and vehicles is still measured in horsepower.
4.) Derivation of the formula: The student goes to the board to derive the formula.
At a constant speed of movement, the body travels a path determined by the formula
We substitute into the original power formula: , we get -
We have obtained another formula for calculating power, which we will use when solving problems.
This formula shows that with a constant engine power, by changing the speed you can change the traction force of the car and vice versa, by changing the speed of the car you can change the traction force of the engine. For N = const v > , F <. v < , F >.
Question: When is greater traction needed? (When going uphill. That's right, then the driver slows down.)
5.) Solving calculation problems: (slide showing the solution at the board.
showing the solution at the board.
6) Question: What is the power of a person? It is believed that the average power of a person during quiet walking is approximately 0.1 hp. i.e. 70 - 90 W. When running and jumping, a person can develop power many times greater. When jumping or running up stairs, a person can develop power up to 730 W, and in some cases even more.
Task: Artem Fedorov and Danya Bogdanov, having heard the bell for class, “rushed” from the dining room to office No. 7 and ran into it at the same time. Did they develop the same power? (No, because the work of gravity acting on each of them was different)
7.) Nature is amazing. An inhabitant of the Ecuadorian forests, one of the representatives of the manakin family - Machaeropterus deliciosus - makes sounds through mechanics, hitting itself on the “back” with its wings. Moreover, he beats himself at a fantastic speed - 106 times per second - this is the fastest movement among vertebrates. Small male manakins demonstrate extraordinary endurance: if the heart rate in the normal state is about 600 beats per minute, then during the dance it rises to 1,300 blows. Among birds, only the hummingbird can boast of such a powerful heart.
Reflection:
Question: How do “living engines” differ from mechanical ones?
Answer: Because “living engines” can change their power several times.
Compiling a syncven.
8.) Summing up. Homework.
Calculate heart power under normal conditions and after physical activity (see sheets)
work.power RAR / 2.45 MB
Lesson summary Work of force. Power. Potential and kinetic energy (grade 10)
Lesson #31
Date:11/18/15
Class: 10
Topic: Work of force. Power. Potential and kinetic energy.
Lesson objectives: Mastering the concepts of work, power, energy, and their units of measurement. Development of an understanding of the practical significance of the quantities being studied.
Lesson type: study and initial consolidation of new knowledge and methods of activity.
Lesson objectives:
1. Educational: Formation of skills and abilities to derive formulas, apply them in solving problems.
2. Developmental: development of the ability to identify patterns, generalize; contribute to the development of students' cognitive interest, logical thinking, development of computational skills, oral speech, memory, attention.
3. Educational: to promote mutual assistance, activity, the ability to communicate, and help each other.
Formed UUD:
Cognitive:
Reproduce knowledge orally and in writing, analyze the conditions of a problem, derive a formula, perform calculations, and the ability to work with various sources of information.
Regulatory:
Determine the goals of educational activities, organize cognitive activity, comprehend the process and result of the activity.
Communicative:
Participate in a collective discussion of a problem, be interested in other people’s opinions and express your own, argue your point of view.
Personal:
Be aware of the incompleteness of knowledge, show interest in new content, show a friendly attitude towards your partner, and show sustained cognitive interest.
Planned results:
Subject:
Knows the formulation and formula: work of force, power, potential and kinetic energy, theorems on kinetic energy, knows how to explain the physical meaning of the studied quantities. Mastering scientific terminology.
Personal:
Using the knowledge gained on the topic to ensure safety when using vehicles, the ability to evaluate the answers of classmates, the formation of value-based attitudes towards each other and the teacher.
Metasubject:
The ability to express units of measurement of physical quantities in SI, give examples of the practical use of physical knowledge about mechanical phenomena and physical laws, establish a logical sequence of existing and acquired knowledge.
Equipment: multimedia complex, presentation for the lesson.
During the classes
I.Organizational moment. Motivation.
II.Checking homework.
- Law of conservation of momentum. An example is jet propulsion.
- No. 352(a)
III. Learning new material
- The concept of mechanical work. A scalar physical quantity that is a spatial characteristic of the action of a force.
A = F·|Δr|·cosα
Unit of measurement: N*m=J
a) A˂0, (example - the work of friction force), b) A>0, (example - the work of gravity when a body falls), c) A = 0 (example - the work of gravity when a satellite moves around the Earth, when moving cars on a horizontal road).
- The concept of power.
A scalar physical quantity characterizing work per unit time.
N=
Unit: =W
- The concept of kinetic energy.
The energy a body has when moving.
=
Depends on the choice of CO. Always non-negative.
Give examples.
A=Δ
- The concept of potential energy.
The energy of interaction between bodies or body parts.
E=mgh. E=
Depends on the relative position of the bodies or the magnitude of elastic deformation.
The zero level is chosen arbitrarily.
Give examples.
- Work of gravity. (Conclusion from the textbook). Video.
- Work of elastic force. (Conclusion from the textbook).
IV. Reinforcing the material learned
Page 139 No. 1 (for strong students)
All students:
Page 134 Unified State Exam to §
V. Lesson summary
Do you know that…
- ... the human heart, pumping blood, performs about 1 J of work per contraction. This work will be enough to lift a 10 kg weight to a height of 1 cm.
- ... the power developed by an adult during normal walking on a level road is 60-65 W. When walking fast, a power of 200 W is already required. For comparison, let’s say that the power of the electric motor of a home coffee grinder is 100-200 W, and that of a meat grinder is 500 W.
Reflection.
Today in class...
VI. Homework: §40-44 exercise. No. 1,2 page 139
For strong students: No. 3, C3 p. 139