Examples for division. Mathematics 4th grade.

So, the topic of addition and subtraction has been mastered, there is a clear understanding of the mathematical operations of multiplication and division, and you can begin dividing numbers in a column. Not every student will understand the meaning of this topic from the first lesson, especially in cases of dividing multi-digit numbers and numbers with a remainder. And here he will need all the support of his parents. To help your child cope with corner division, use our theoretical tips. The article has a detailed explanation of the process of solving examples, as well as accessible visual illustrations.

How to learn to divide by column 3rd grade

Arithmetic calculations in grade 3 are based on the multiplication table from 1 to 10 within numbers up to 100. At this stage, the child must understand the division process itself and accurately identify the categories of “divisor,” “dividend,” and “quotient.” Of course, the easiest way to divide multi-digit numbers is by column. The student is less confused and does not lose numbers. Thus, a mental logical scheme is developed. The essence of the method cannot be grasped without knowledge of the multiplication table and the method of “reverse” division.

Column division algorithm

For example, 98 must be divided into a column by 7.

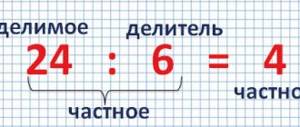
In our example, 98 is the dividend, 7 is the divisor, and the resulting division result is the quotient. It is necessary to find him.

We write the dividend and divisor side by side, dividing them with a vertical line with a corner. Now you need to determine how many sevens will fit in a nine - one. We will write the number “1” under the line in the lower right corner.

Under the nine we write a seven, underline it with a line, subtract and write down the difference - 2. If not a single seven fits in a two, then the solution is correct. Let's take the top eight to the two. We get - 28. Let's analyze how many sevens can fit in the number "28" - 4. We write the resulting answer next to "1".

From 28 we subtract the number “28” and get “0” - which means the division was done correctly. If the result of division does not result in zero, there may be an arithmetic error in the calculations or division without a remainder is impossible. As a result, the quotient turned out to be “14”.

The correctness of the division can be checked if, when multiplying 14 by 7, the result is 98 - the calculations are correct.

The main problem that third-graders face in mathematics lessons is the lack of ability to perform quick arithmetic operations. But the entire elementary school curriculum is based on this basis, especially division operations.

General information

Any mathematical operation can be carried out in a column. Division is no exception. It should be noted that it happens without a trace and with it. If the first type of operation is performed, then it is necessary to know the signs of division. The latter are the rules by which you can determine whether a number is divisible by another without a remainder. However, in the second case, a certain value is obtained at the end of the calculation. Mathematicians call it a remainder.

This type of division is widely used in programming languages to create various conditions. If you need to perform a column division by a single-digit number without a remainder, then you need to know the signs of divisibility. The latter are not needed in the case when a three-digit number with a remainder must be divided by a single-digit number. It should be noted that terminology needs to be differentiated. Not all people know the basic difference between numbers and numbers. The first are used to form the second, that is, the first are a set of signs.

The main requirement necessary to carry out this operation is a thorough knowledge of the multiplication table. Not a single lesson, written report assignment or exam is complete without the latter. The division operation is used less frequently than addition, subtraction or multiplication. However, you should know it thoroughly and be able to make calculations not only using a calculator or computer, but also manually.

Sometimes students are faced with a misunderstanding of material that the teacher cannot clearly explain to each individual. If a child has problems in any academic quarter, then you should not delay in solving the problem. Parents need to develop their own learning system or use a ready-made one. However, some of them begin to shout at the child, traumatizing the psyche. It should be remembered that he often copies the behavior of his parents. When they teach him to solve problems emotionally, then young people who lack self-confidence grow up.

It should be remembered that studying any exact science requires patience. Even famous mathematicians failed to achieve anything right away. It is necessary to create a cozy corner at home with exercise equipment for training in solving mathematical problems. Let this be a kind of office for the baby. He needs help equipping it: printing out the necessary mathematical material and making good lighting.

How to learn to divide by column 4th grade

The 4th grade program, compared to the previous academic year, is becoming more complicated in the direction of increasing the estimated numbers. Fourth graders divide multi-digit numbers greater than 100. They learn to divide numbers with a two- and three-digit divisor with a corner, as well as solve examples with a remainder. The algorithm for solving corner division is similar to the algorithm studied in third grade.

Let's, as an example, divide 1072 by 8 . You immediately need to decide on the division categories: 1072 is the dividend, 8 is the divisor. The result obtained as an action is a quotient. Let's write the numbers on both sides of the corner. Let's immediately decide on a number that is greater than the divisor itself. 1<8, so start the action with 10. This number can contain only one 8. Let's write the result in the right column.

We multiply the divisor 8 by 1 and get - 8. We sign the result under the dividend 1072 and subtract it. The resulting number is 2<8, so we will increase it using the next unused dividend number - 7. The result will be the number “27”. Then they act according to the algorithm. Let’s analyze how many eights the number “27” contains. It contains 3 x 8 = 24. We will add the number “3” in the right column next to the quotient 1. At the moment, the quotient is 13. To the left of 27 – 24 = 3.

The last number of the quotient will be “32”, due to the unused divisor. Having analyzed the number, we write down the result: 32: 8 = 4. We add the resulting 4 to the quotient - 134. All that remains is to check the result: 134 x 8 = 1072.

How to learn to divide by two digits

In the 4th grade, the student should be able to divide multi-digit values into two- and three-digit numbers with a corner. The acquired skill is necessary for further mathematics courses up to 11th grade. Of course, such a division is more complicated than an unambiguous one, but with the right approach and understanding it will not be difficult. What is important here is the correct selection of numbers and gradual mastery of the topic, from simple to complex.

For example, let's perform the action: 144 : 24

As in the case of single-valued division, we define a number greater than the divisor itself: 14<24, i.e. Let's divide the whole number at once - 144. Let's estimate 144:20, we get about 7. The trial number is not yet written in the column. Let's check, 7 x 24 = 168, which is significantly greater than our dividend. Let's take 6 x 24 = 144 - this is our number. Let's sign it under the dividend and get the answer - 6.

After gradually mastering simple examples, you can move on to more complex ones.

Divide 1035 by 23.

Having determined the first digit, 103 > 23, we divide it by 23. 20 x 5 = 100, but in our example we have 23 x 5 = 115, which is more than 103. Let’s take 4 each: 23 x 4 = 92. Write the answer in the right column under line. From 103 – 92 = 11. We will write the data under the dividend. 11<23, i.e. the calculations were made correctly. By 11 we take away 5 and get the number “115”. Using the selection method, we determine the result: 23 x 5 = 115. We write the number “5” next to 4 in the answer – 45. Let’s check: 45 x 23 = 1035, the result is correct.

Divide by any multi-digit numbers (three-digit, four-digit, etc.) in the same way.

How to learn long division with a remainder

Division with a remainder is the next stage of learning. During such actions, the dividend cannot be evenly divided into parts. The example answer will have an indivisible piece smaller than the divisor. In order for the student to quickly understand the meaning of mathematical operations, the topic is explained using accessible examples. There are 34 candies on the tray, which need to be divided among 8 children. When each child receives 4 candies, there will be 2 more pieces left on the table. This will be the remainder. The calculations look like this: 34: 8= 4 rest (2). Where did the number "2" come from? 8 x 4 = 32, 34 - 32 = 2. The principle of dividing by a corner with a remainder is similar to the classical one, with one difference - the presence of a remainder.

For example, divide 235 by 14.

235 - the dividend, we will place it on the left, we will write the divisor (14) to the right. Let's separate both values with a corner. Let's start looking for the whole. 23>14, this number contains 1 divisor. We will write the unit below under the corner. 23 - 14 = 9.

To 9 we take 5 - the number of units of the dividend and as a result we get the second incomplete dividend - 95. Using the selection method we divide 90: 10 = 9, but in our case 14 x 9 = 126, which is more than 95. Let's try 14 x 8 = 112. 112> 95, so let's take one less: 7 x 14 = 98, which is also two units more than 96. Now we know for sure that the required number is 6: 6 x 14 = 84 95 - 84 = 11, i.e. 11 is the remainder.

When solving examples with a remainder, the answer can be written in two ways:

in the form of a fraction, when the remainder is placed in the numerator, and the divisor is written in the denominator: 11/16,
but most often the answer is written in words: 6 whole and 11 remainder.

How to learn to divide three-digit numbers with a column

When the divisor contains a three-digit number, the action is best performed in a column. The mathematical solution algorithm is similar to division by a two-digit number.

For example, consider the following actions: 146676 : 719

146<719, so let’s immediately take the four-digit number “1466”. This value contains 2 divisors: 719 x 2 = 1438. The number “2” will be the first value of the quotient. Let's write it on the right under the corner.

1466 - 1438 = 28. We write the resulting difference under the line on the left. Let's add the number "7" to 28. 287<719, so next to the two we’ll write “0”.

Let’s take away the last digit of the dividend “6”, the result will be the number “2876”, which we will divide by 719. Let’s take 3 each: 719 x 3 = 2157 - not enough, you can take 4 each: 719 x 4 = 2876. Write the number “4” next to it with “20”, we get 204 in answer. Subtract 2876 from 2876, we get a difference of 0.

It is advisable to check at the end whether the actions were performed correctly: 204 x 719 = 146676. The answer is correct.

Prime and composite numbers

Numerical values in mathematics are divided into simple and composite. The mistake many beginners make when solving problems is that many of them do not know about the existence of special tables. There are two ways to “recognize” a prime number:

Manual.
Tabular.

The first method is recommended to be used when it is not possible to determine a prime number using a table or a computer (computer). For these purposes, there is a special algorithm, which consists of a set of steps to find the divisor. It looks like this:

Enumerate all the factors.
Write down the result or make sure the number is prime.

It is simple, but to understand its mathematical meaning, you should look at a specific example for the number 5678913 . The task must be solved according to the following scheme:

1: divisible, that is, 5678913 / 1 = 5678913.
2: not even. Therefore, this divisor does not exist.
3: 5 + 6 + 7 + 8 + 9 + 1 + 3 = 39 = 3 + 9 = 12 (divisible).
4: There is no factor because 13 is not divisible by 4.
5: the number does not end in 0 or 5 (not divisible).
6: the sum of the digits is 12, and is divisible by 2 and 3 (divisible).
7: 5|678|913 = 6 + 7 + 8 + 9 + 1 + 3 = 34 (no divisor).
8: 913 is not divisible by 8, 4 and 2.
9: not divisible because the sum of the digits is equivalent to 12.

When you need to prove that a number is prime, then you can complete the exercise in the third step. This requires a minimum number of operations, since there is no point in performing them further. If the essence of the solution is to find divisors, then it can be continued up to point 9 inclusive.

We can conclude that the original number is composite. However, there is a whole algorithm for dividing by a single-digit number with a column or factoring. For a three-digit number everything is quite simple.

How to learn to divide multi-digit numbers into a column

The stages of long division of a multi-digit number are similar to the classical division of a multi-digit number by a single-digit number.
In the first case, we take into account only the first digit of the divisor, and when dividing by a multi-digit one, we take into account the number of all digits of the divisor. The working number must be greater than the divisor. In other cases, we add the next digit and divide according to the algorithm class=”aligncenter” width=”800″ height=”600″[/img] Mathematical operations for long division will be within the power of a student if he understands the basic calculation algorithm. The correctness of the solution can always be checked by multiplication.

Column division method

There is a specific algorithm for long division. It is studied in the primary grades of secondary schools. The technique can be used not only for positive but also negative values. In this case, you need to take into account the sign:

Dividing a negative value by a negative value is a positive value.
When dividing a positive by a negative or vice versa - a negative value.

There are 2 types of operation: with and without remainder. In the first case, the result is written as an integer value and a remainder, and in the second, it is only an integer value.

Algorithm without remainder

The technique is used when the dividend is not a prime number, but contains factors. In addition, when it is divided by a divisor that does not correspond to one of the division signs. For example, 33 is divisible by 2 with a remainder. However, when the divisor is 3, then the latter is missing.

To apply the algorithm, you need to clearly understand the following example: you need to divide 78 by 2. The methodology for performing this operation is as follows:

Write the dividend on the left side and the divisor on the right.
Using the prime numbers card or using the manual method, you need to determine whether the dividend is a prime value (78 is divisible by 2 because it ends with an even digit 8).
Separate two values with a vertical bar.
Select I incomplete dividend: 7.
Using the multiplication table, select the nearest integer (3). When multiplied by a divisor, the result should be a value that is less than the first incomplete dividend (3 * 2 = 6 < 7). If we write 4, then 4 * 2 = 8 > 7 (this option is not suitable).
Write the number obtained by multiplying the divisor by the selected value under I incomplete dividend. Perform the subtraction operation (7 - 6 = 1).
The result of subtraction (1), which is called the remainder, is not divisible by 2. Therefore, it is necessary to add II incomplete dividend (18). If for some reason the result is divided by the divisor, then the selected value is incorrect.
The value 18 is divided by 2, i.e. 18/2 = 9.
The result of dividing 78 by 2 is 39.

The correctness of the operation can be checked by multiplying the result by a factor, i.e. 39 * 2 = 78.

Operation with balance

Not in all cases the result of dividing two numbers is an integer. In the school curriculum there is a group of examples in which you need to find the remainder obtained by dividing 2 values (77/3). The algorithm is similar to the previous one, but there are some features:

Two numbers are written as in the previous case.
Membership in the set of prime numbers is not checked.
Select I incomplete dividend: 7.
Find the nearest integer, writing it into the result: 2.
Check: 3 * 2 = 6 < 7 (value is correct).
Write 6 under 7, and then perform the subtraction operation: 7 - 6 = 1. The remainder is less than 3, therefore, the number is chosen correctly.
Select the multiplier for 17: there is no integer value. Therefore, you need to choose the nearest integer: 5.
Check: 3 * 5 = 15 < 17.
Write 5 into the result and determine the remainder: 17 - 15 = 2.
The result of dividing 77 by 3 is equivalent to: 25 with a remainder of 2.

Thus, to perform the operation of dividing a two-digit number by a single-digit number, you need to know the signs of divisibility of quantities, as well as the basic algorithms for division with and without a remainder.