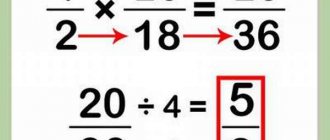Outline of a mathematics lesson on the topic “Division of fractions”, grade 6
Math lesson in 6th grade
Teacher: A. V. Palko
Lesson topic:
Dividing fractions.
Lesson type:
- for the main didactic goal: a lesson in learning new material using ICT
- according to the main method of conducting: a combination of various forms of classes;
- on the main stages of the educational process: a lesson in the formation of concepts, the establishment of laws and rules;
- according to the form of delivery: combined lesson;
- on the target setting: lesson-research.
Lesson objectives:
- form an idea of dividing ordinary fractions, develop the primary ability to divide numbers written in the form of fractions;
- developing – development of thinking (the teacher sets students a task for which the students do not yet have the necessary knowledge), memory development (at the stage of updating basic knowledge and methods of action); develop research skills; graphic culture of students;
- educational - the formation of educational-communicative, educational-intellectual skills, cultivating interest in the study of mathematics, cultivating a focused attitude to activity, accuracy, observation, interest in surrounding phenomena.
General teaching methods:
- by source of knowledge: conversation (students talked with the teacher at different stages of the lesson), demonstration method (showing a presentation), exercises;
- by the nature of cognitive activity: explanatory and illustrative (the teacher explained new material, supporting new data with examples on the board and demonstrating a presentation with visual examples), reproductive (students performed actions according to the model), problem-solving (at the stage of solving creative problems), research (at the stage studying new material to develop the primary ability to divide numbers written as fractions).
Special teaching methods: analysis, synthesis (when students solve new tasks).
Forms of training: group, individual.
Equipment: board, computer, projector, presentation.
Lesson steps:
- Organizational moment (1 min) and motivation
- Updating basic knowledge and methods of action (5 min).
- Introduction to new material (15 min).
- Consolidation of new material (20 min).
- Summing up the lesson (3 min).
- Setting homework (1 min).
During the classes.
1.Organization of the beginning of the lesson and motivation. (
Providing motivation)
The outstanding French philosopher and scientist Blaise Pascal argued: “The greatness of a person is in his ability to think.” Today we will try to feel like great people by discovering knowledge for ourselves.
The motto for today's lesson will be the words of the ancient Greek mathematician Thales:
- What is more than anything in the world? - Space.
-What's the fastest? - Mind.
-What is the wisest thing? - Time.
- What is the most pleasant thing? - Achieve what you want.
I would like each of you to achieve the desired result in today’s lesson.
2.
Today we are waiting for an exciting journey into the kingdom of mathematics. Three teams go on a trip (30 seconds to name the teams, team No. 1, captain, etc.). Along the way, we will face many tests, after which we will gain new knowledge.
Tell me, do you like fairy tales? Let's try to compose our own fairy tale. How do most fairy tales begin? Once upon a time there were ordinary fractions. They were regular and incorrect, as well as mixed, reducible and irreducible, and also mutually inverse.
Slide 2. Find the fraction.
The first team is looking for improper fractions, the second is correct, the third is mixed. They go out and write it down on the board. (4 fractions each)
They lived together and learned to perform various actions.
Slide 3. Updating basic knowledge and methods of action.
Task No. 1 from the collection of preparations for the OGE, find the meaning of the expression. Two students participate from each team. The task is considered completed when the last team member solves two examples. We start on the left.
Key: 1 team (79 1/5; 3 1/12;), 2 team (58 2/5; 11/45;), 3 team (2 3/4; 1 17/20;)
But one action was enchanted. Ordinary fractions could not apply this action in any way. What action is this? DIVISION is correct. Formulate the topic of the lesson: “Division of fractions” Slide 4. Write the topic in a notebook.
3. Determining the objectives of the lesson.
(slide number 5).
Each team names at least two goals. 1. We will get acquainted with ... (dividing fractions)
2. We will learn... (how to divide ordinary fractions)
3. We will remember...(covered material)
4. We will be able to...(solve division problems)
5. We will be able to reflect...(on difficult tasks)
Historical reference.
(slide number 6)
Let's dive into history a little. “Multiplication is my torment, and division is trouble,” the schoolchildren of the 15th...16th centuries mourned.
Although multiplication in the old days was considered difficult, division was even more difficult. In the Middle Ages, people who knew how to perform division could be counted almost on one hand. They moved from city to city at the invitation of merchants who wanted to get their accounts in order.
They were respectfully called "Masters of Division".
Division rule. (slide number 7)
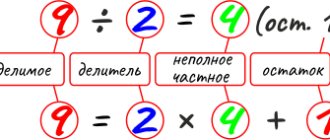
To divide one fraction by another, you must multiply the dividend by the reciprocal of the divisor.
5. Physical exercise (slide no.
Children are given instructions: “Sit more comfortably, close your eyes. Imagine that you are lying in a beautiful clearing. Take a deep breath and exhale slowly, letting all the tension go away. There is green grass all around, a large forest in the distance, birds are singing. You feel how warm the earth is. The bright sun is shining. It feels good and pleasant to bask in the sun. There is green grass all around, a large forest in the distance, birds are singing. You feel how warm the earth is. The earth gives you strength and confidence. Take a deep breath and exhale slowly, letting all the tension go away. Inhale and exhale again... At the count of 5 you will return back. 1 – you feel how good it is to lie down and relax. 2,3,4 – your eyes open, 5 – you return to the lesson full of strength and confidence.
6. Consolidation of the studied material.
(slide number 9)
Russian writer Lev Nikolaevich Tolstoy said: “Knowledge is a tool, not a goal.”
Let's learn to use the knowledge you have acquired today as a tool to complete tasks of a different nature.
Work from the textbook - No. 596
7. Summing up the lesson.
(slide number 10)
Each team worked hard today. While performing various tasks, you sometimes made mistakes. And this is not surprising, any person is not immune from mistakes, especially when he is just learning to master any science. It is important to find and correct these errors in time, understand why they appeared, and try to prevent them in the future.
Parable:
A sage was walking, and three people met him, carrying carts with stones for construction under the hot sun. The sage stopped and asked each one a question. The first one asked, “What have you been doing all day? And he answered with a grin that he had been carrying stones all day. The sage asked the second, “What did you do all day?” and he replied, “And I did my job conscientiously.” And the third smiled, his face lit up with joy and pleasure, “And I took part in the construction of the temple.”
- Guys, let's try to evaluate each of your work for the lesson.
—Who carried the stones? (raise red tokens)
-Who worked conscientiously? (raise yellow tokens)
—Who built the temple? (raise green tokens)
Team captains are asked to rate their team members; while they are rating, we repeat the division rule again.
8. Homework.
(slide No. 11)
● Complete exercises No. 596 (g-l);
Creative task: make up a problem with division elements.
Summary of a mathematics lesson on the topic “Division of fractions”, grade 6
Math lesson notes
Teacher: Barmina Oksana Vladimirovna
Class: 6
Topic : Dividing fractions
Lesson type : learning new material
Forms of work in the lesson : individual, pair, group, whole class
Goals:
Subject : introduce the rule for dividing ordinary fractions; introduce the algorithm for applying the division rule in practice.
Personal : development of a subjective position in educational activities, development of cognitive needs.
Goals related to the formation of universal educational activities:
Cognitive: developing the ability to put forward hypotheses, developing the ability to model;
the ability to consciously and voluntarily construct a speech statement in oral and written form.
Regulatory: developing the ability to perform goal setting as setting an educational task based on the correlation of what is already known and learned by the student and what is still unknown; developing the ability to plan - determine the sequence of intermediate goals, taking into account the final result; the ability to draw up a plan and determine the sequence of actions.
Communication: develop the ability to listen and engage in dialogue, participate in collective discussion of problems, integrate into a peer group and productively interact and collaborate with peers and adults.
I.Organized start of the lesson.
Every mathematics lesson we begin with you to discuss the importance of studying it. And not only for the sake of mathematics, but in general for your successful future life.
If you want to participate in a big life, then fill your head with mathematics while you have the opportunity. She will then provide you with great assistance in all your work.
I suggest you now lay a new brick in a solid foundation on which your entire future life will be built.
II.Updating .
- What do you think: who has been the main character of our lessons for 2 months? (student reads verse)
Anyone can see the fractional line from a mile away. Above the line is the numerator, you know, Below the line is the denominator! Such a fraction must certainly be called ordinary. Simply multiply a fraction by a fraction: You need to multiply the numerators and denominators!
- From the very beginning of the school year, we are revealing to you the secret of operations with ordinary fractions.
I suggest you check how well we managed to uncover this secret. Everyone's favorite holiday, New Year, is coming soon. Therefore, I decided not to just give you tasks, but prepared this spruce branch with Christmas tree decorations.
We complete the task, if we agree with the answer, then we paint over the ball, if not, then we leave the ball.
The teacher clarifies the task out loud. Students complete assignments independently.
Checking the correct execution (finished picture on the screen)
Execution correction.
3) Now I suggest you complete a number of tasks so that our heads are ready to work at the highest level.
-Find the value of the quotient if the divisor is 7 and the dividend is 280.
-The side of a square is ¼ inch. Find the area and perimeter of the square.
— The kindergarten bought 4 m of fabric for sewing costumes. 6 girls will take part in the dance. How long will each girl's scarf be?
3) What action will we use to solve the problem? Do we know the rule for dividing ordinary fractions? (No)
So, what knowledge are we going to discover? (knowledge of the rule for dividing ordinary fractions)
III . Goal setting and motivation .
What is the main value of our lesson today? (learn the rule and learn to apply it when performing practical tasks)
Why do we need to discover this new knowledge (be able to solve practical problems in everyday life)
To achieve success in any activity, you need to clearly plan your activities. We will also determine the sequence of actions. (on the slide - together we discuss the stages of work, talk through them)
IV. Learning new material.
- The easiest way is to get a ready answer to the question, but it is not the most effective. I suggest you try to discover new knowledge yourself. To do this, you will need to complete a number of tasks following the instructions. We work in groups. Choose a captain. The captain clearly distributes responsibilities during the work. Time to work 5 minutes.
(all children are divided into 6 groups according to the level of development of mathematical abilities: groups 1a and 1b have developed logical thinking, have a “5” in mathematics; groups 2a and 2b have an average level of mathematical abilities, have “more often than 4” in mathematics; 3a and 3b - These groups included students who often have a "3" or "2" and are able to perform only tasks at the reproductive level. Students in this group do not know how to work in a group, so first they each complete tasks independently, then unite for discussion. Therefore, everyone groups of tasks are compiled on the basis of a differentiated approach. Cards with instructions in the Appendix)
During group work, the teacher plays the role of curator and activity coordinator.
2.) Now I invite you to present the results of your work. We start with groups No. 3, then group No. 2, then group No. 1. (this is necessary so that groups No. 1 can summarize and draw a conclusion)
3.) We need to clearly understand the sequence of actions when dividing ordinary fractions, so I suggest you use cards to model the situation discussed in the rule (pair work - collect fractions from numbers, example for division, then swap the numerator and denominator in the divisor) Actions are accompanied by display at the presentation.
Now I invite you to do a creative task: using the same set of cards, create an example for division so that the value of the quotient is the same as in the previous example. (work in pairs)
4.) I think we are ready to solve the problematic problem that arose at the beginning of the lesson. So, let's return to solving the problem. Let's analyze all the numbers with which we need to perform an action. What can you say? Compare. Find similarities and differences. (general class form of work)
The problem contains a mixed number. Will we be able to use new knowledge to solve this problem? What transformations need to be made? Let's remember: how to represent a mixed number as an improper fraction. How to find the inverse of a natural number? (students answer teacher's questions)
Try to formulate a solution to the problem while working in a group. Write down the solution on an A2 sheet of paper with a marker. Time to work 3 minutes.
So let's see. What solutions did you come up with? (Team captains come out to the board with sheets of paper) We check the solutions. Write down the correct solution in your notebook.
5.) It is very useful to strive to discover new knowledge yourself. When something works out, you feel satisfied that you did it. And this is so great!
Now let's see where you could find information about the rule for dividing fractions or where you can find information if you need to review. (work according to the textbook p. 17 p. 97, the teacher pays attention to the section “speak correctly” p. 98)
6) We learned the rule. What needs to be done now? (students assume that they need to learn how to apply it in practice)
No. 596 (a, b, f, g) display of design at the blackboard, all other students in notebooks.
Additional task for children:
No. 596 (c, d, d, j) independently in notebooks (the teacher works individually with students experiencing difficulties)
№ 603.
7) And now I suggest you check for everyone the effectiveness of their work in class. I suggest using a New Year's card for this work. Read the assignment carefully. (perform examples on the card, then you need to connect the answers with the numbers in the squares, then correlate them with the words in the rectangle. Creative task: try to compose a continuation of the poem read at the beginning of the lesson.)
Checking progress. Reading a poem.
It’s not difficult to divide fractions: All you have to do is replace the second one with a fraction, its inverse – And it’s pleasant for us.
V. Summing up. Homework. Reflection.
Analyze all the examples that we have now solved. Please tell me, is it possible to say that we are already fluent in dividing fractions? What examples will we need to pay attention to in the next lesson? (dividing mixed numbers) And then? (you must learn to apply this skill to solving problems, equations and other tasks.
So that we can move on in the next lessons, what needs to be done at home? (learn the rule, practice applying it)
To do this you need: 1.p.17 from 97-98 No. 633 (a,b,c,d,e) 2. Draw a picture on sheet A4 that illustrates the rule for dividing fractions.
What word did we have left unused when composing the poem? (Persistence.) This means that if we are persistent and diligent in achieving our goals, then all our dreams and desires will come true!
They say: on New Year's Eve, whatever you want, Everything will always happen, Everything will always come true.
Even the boys can have all their wishes come true, they just need to make an effort.
I suggest that you don't just hand in the New Year's card, but write on the other side what you would like to say or ask your teacher. This can be 1 word, phrase, sentence.
Thank you for the lesson!