At first glance, the Pythagorean table is large and incomprehensible. You look at her and throw up your hands - how can you remember all this?!
No need to panic! It’s worth first looking at it carefully.
After all, the whole trick of the Pythagorean table is that the patterns are clearly visible on it!
That is why it makes memorizing the multiplication table easy and quick.
These are the ones we will mainly remember.
But first, we need to find these patterns.
By the way, perhaps now you want
First observation, or minus half the table
Upon closer examination, it turns out that the bottom half of the plate, if folded along the crimson diagonal, mirrors the top.
Why is that? Did you guess it? That's right - because
2 x 5 = 5 x 2
well and
8 x 7 = 7 x 8
This means that we only need to learn half of the table. It's already twice as easy!
Let's look further
Easy ways to remember
When preparing for classes, you need to stock up on everything you need - checkered paper, pencils, markers, colored pens, stickers. You can draw a multiplication table on paper, highlighting the numbers in bright colors.
Examples are written on stickers, and separately - the results of the work in the form of a series of answers that the child will have to choose.
Using the Pythagorean Table
The Pythagorean table, which can be found on simple checkered notebooks, consists of 100 cells. For convenience, their number can be reduced by leaving the space for the result of multiplication by 1 empty by default.
In simplified form, the table will look like this:
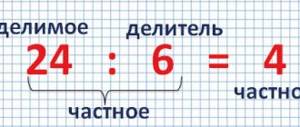
Learning the multiplication table is a common problem that arises among elementary school students.
The child must understand that the results of multiplication are located at the intersection of each column and row. First, you need to memorize simple examples, gradually moving to a more complex level.
Highlighting identical values
Identical numbers in the table can be highlighted with 1 color, showing the child that they are obtained as a result of the product of identical factors, but rearranged.
Pythagoras's table of colors.
This will help form a logical relationship in your mind.
The child will only have to learn half of the Pythagorean table; he can calculate the rest himself.
Learning through games
It is recommended to use crosswords, coloring books, labyrinths, and puzzles.
Popular memory games:
"Building a fence"
The Fence exercise will help you visualize how multiplication works.
The child needs to calculate the number of nails needed to attach n-number of beams to the boards using multiplication.
"Fishing". Players roll a dice that lands on a picture with a certain number of fish. All the cards (fish) are added up, and then the winner is determined by making the biggest catch.
Game field "Fishing"
"Battle" on a printed Pythagorean table. Parents and the baby take turns making moves, occupying the cells with a treasure trove of chips. The greater the result of the product, the more coins the player manages to get.
You can click on the picture (to enlarge) and download/print the playing field:
Playing field
Filling out the Pythagorean tablet . Print out a blank sign for your child and ask them to fill in the boxes themselves using a simple addition action.
Filling example:
In the pairs game "Rectangle", participants use a piece of checkered paper, 2 multi-colored markers and 2 cubes. Each player takes turns: rolls 2 dice, and then draws a rectangle on his side, the number of cells in which coincides with the number of dots on the die. A number is written inside the resulting figure - its area, calculated from the cells.
The game continues as long as there is free space on the sheet. At the end, the one with the most pieces wins.
On the Internet you can find educational online games for studying the Pythagorean table. An example of one interactive charade: the columns hide an encrypted phrase, which the child can guess by making the necessary calculations.
Another educational game set, “Many, Many,” will help children learn the multiplication tables in a visual way. It contains cards in the form of houses with transparent windows. By connecting them to each other, you can calculate the resulting number of windows: 2x4=8, 3x2=6, etc.
On fingers
Multiplying by 9 is the most difficult thing to do, but you can explain to a child how to do it on your fingers. To count, turn your palms towards you and mentally number all your fingers using numbers from 1 to 10. If you need to multiply 9 by 1, bend the first finger on your left hand - the result is determined by the number of fingers remaining straightened.
If you need to calculate how many “9x5” there will be, remove the 5th finger of the left hand, if you look from left to right: the first 4 fingers will serve as tens, the remaining ones will be ones. The resulting number is 45.
Multiplying by 9 on your fingers
Multiplying by 9 from 1 to 10
Learning with Flashcards
Flashcards will help you remember information visually. They can be cut out of thick cardboard in the form of squares. Examples are written on cards and then placed in a cloth bag.
The child needs to take out pieces of paper one by one and determine the product of numbers. If the answer is correct, the memorized card is removed to the side; otherwise, it is returned to the general pile. In case of an error, it is necessary to name the correct answer so that it is fixed in the child’s memory.
You can
The game develops interest in learning arithmetic, helps to remember and consolidate information through repetition.
Learning through Poetry
Short poems with arithmetic operations are easy for children to remember:
- “2 athletes took weights: this is 2x2=4.”
- "Twice 7 mice - 14 ears."
- “Two elephants need to be weighed - 2 by 5 equals 10, which means that the elephant weighs approximately 5 tons.”
- “The mice gnawed holes in the cheese - 3x8 makes 24.”
- “The hares went out into the forest for a walk - 5x5=25.”
Multiplying a number by itself in verses
By composing these rhymes, parents will be able to quickly teach their child multiplication - the learned verses will remain in memory for a long time.
A few more nursery rhymes for remembering multiplication results:
Multiplying by three and four
There are no special secrets here. Simply multiplying by three means adding it again to a number multiplied by two.
That is, 2 x 3 = 4 + 2, and 6 x 3 = 12 + 6, etc.
Well, to multiply by four, you need to add the result of multiplying by two with itself.
2 x 4 = 4 + 4, and 6 x 4 = 12 + 12
In a word, to multiply by three and four, you need to be able to quickly remember multiplying by two.
Here I strongly advise you to draw a lot of empty Pythagorean tables and gradually fill them in. Those cells that you already know - how.
How to quickly and easily learn the multiplication table: the best ways
Here are some easy-to-understand and great-working ways to learn the multiplication tables with your child:
Pythagorean table
The multiplication table diagram, which is classic for Russian education, can be intimidating because of its volume - it turns out that the student will have to learn as many as a hundred examples.
Replace the usual table with the Pythagorean table, and instead of 100 arithmetic operations, you will only have to remember 36.
How to master multiplication using the Pythagorean table:
1. Make a Pythagorean table showing only the factors.
2. Together with your child, fill in the empty cells. A junior student can cope with many examples on his own. Tell them that it is enough to add 2 and 2, and then add 2 to each resulting sum: 2 + 2 = 4, 4 + 2 = 6, 6 + 2 = 8, etc.
In the same way, fill in the cells with the remaining factors: 3 + 3 = 6, 6 + 3 = 9; 4 + 4 = 8, 8 + 4 = 12, etc.
3. Draw the child’s attention to the fact that, similar to the principle of addition, in multiplication, changing the factors does not change the result: for example, if you multiply the numbers 4 by 6 or 6 by 4, you get 24 in both cases.
4. Help your son or daughter come to the conclusion that almost half of the examples are repeated, only the factors are swapped - all that remains is to remember 55 examples instead of 100 .
5. Tell me other patterns that do not need to be memorized:
- a number multiplied by one remains equal to itself;
- when multiplying by 10, it is enough to add 0 to the number to get the correct answer (2 x 10 = 20, 3 x 10 = 30, etc.).
By studying the multiplication table using the Pythagorean table, the child will only have to learn 36 examples instead of a hundred.
Multiplication cards
You can use ready-made cards or make them yourself - this way the child will begin to memorize the table immediately in the process of preparing the cards.
How to learn a table using flashcards:
- on a small sheet of paper the child writes the action, on the back of the same sheet - the correct answer (for example, on the front side - 6 x 7, on the back - 42);
- You can write down all the examples from the table on cards, and later leave only those that cause difficulties for the child;
- add game elements to your training: you can set a goal to give one hundred correct answers out of a hundred or name the results of multiplication by speed.
Board games
This method is especially suitable for restless children: fairly complex information is gradually memorized in the form of an entertaining game. You can use ready-made games that are built on the principles of multiplication or multiplication and division (division will also be studied in the second grade). For example, the board game “Many, Many” or “Tsvetarium”.
Another option is to play regular “walkers” with modified rules: agree that the rolled number of moves will be multiplied by 2, 3 or any other number less than or equal to 10.
From simple to complex
Children remember the table more easily when they learn examples not in a row, but move from simple to more difficult ones. Try learning multiplication in this order:
- units and tens: the simplest examples, with which there are usually no problems (a number multiplied by 1 remains the same; multiplied by 10, 0 is added);
- by 5: multiplying an even number by 5 will necessarily result in an even number ending in zero (2 x 5 = 10, 4 x 5 = 20), multiplying an odd number by 5 will result in an odd number ending in 5 (7 x 5 = 35 , 9 x 5 = 45);
- by 2 and by 4: multiplying by 2 is always the same number added to itself (2 x 2 = 4, 3 x 2 = 6); by 4 - the same as multiplying by 2, but doubled, that is, you can multiply a number by 2 and add the same number to it (2 x 4 = 2 x 2 + 4 = 8);
- by 9. The easiest way to remember is with your fingers:
- have the child turn his palms up and mentally number his fingers from 1 to 10, counting from left to right (starting with the thumb of his left hand),
- ask the child to bend the finger that corresponds to the number multiplied by 9,
- for example, when multiplying 3 by 9, you need to bend the third finger from the left, the remaining two fingers on the left are tens, the seven fingers on the right are ones, the result is 3 x 9 = 27;
- for 3, 6, 7, 8: you can learn by heart or use other methods - cards, posters, rhymes, board games, try learning with your fingers.
Multiplying by 9 using your fingers. Photo source: https://kunduz.com/tr_tr/blog/bolme-bolunebilme-konu-anlatimi-ve-ornek-soru-cozumu-6169/
Multiplying by five
Let's move on to multiplying by five. Why five? Because there is a trick about five.
So. Look at the multiplication by five column. Do you see what we have there?
Yes. We either have a round number (one that ends in zero) or one with a five at the end. Each subsequent number is five more than the previous one.
And now here’s another trick Marina and I discovered:
If we multiply five by an even number, the result is round. If it's odd, the result is a five at the end.
Plus one more secret - for even numbers, to get the first digit, you need to divide the number by two.
That is:
If we need to multiply 6 by 5. What we do:
The first one is six even, which means there is a zero at the end.
The second is 6 divided by two - 3. So in the beginning - three!
So, 6 by 5 will be 30!
And, of course, remember that five equals twenty-five! It's just some kind of song!
Now that we already know multiplication by 2, 3, 4, and 5, it’s definitely time to fill out our table and see how much is left to learn?
Yes! Fill in not only columns 2,3, 4, 5, but also lines 2, 3, 4, and 5.
Well, what do you see? There’s almost nothing left to learn!
Presentation on the topic Pythagorean table
Project stages
Determine the purpose of the project. Define the project problem. Relevance of the project. Explanation of the concept of Pythagorean Square. History of the Pythagorean Square. Calculation of Pythagorean Square using an example. The value of the final data as a result of calculating the Pythagorean Square. Calculation of the psychomatrix of our classmates and the class teacher using the Pythagorean Square. Understand how much your date of birth influences your choice of profession. Receive the final product of the project.
Slide 4
Project methods
1) Collecting information 2) Surveying students 3) Creating a presentation 4) Calculating the Pythagorean Square 5) Creating a project product
Slide 5
Objective of the project:
Determine whether a person belongs to the technical or humanities sciences, based on individual numbers obtained by calculating the Pythagorean square.
Slide 6
Project problem
We chose this topic because the problem of choosing a profession is very common today. In the modern understanding, the meaning of career guidance work is the gradual formation in a teenager of an internal readiness for conscious planning, adjusting his professional plans and interests. And the Pythagorean Square is needed so that no one makes a mistake in choosing the profession that best suits his natural talent.
Slide 7
Relevance of the project
Today, many students do not know which high school profile to choose. This project should help students and teachers determine the future direction of their activities and identify the characteristics of their character.
Slide 8
The concept of the Pythagorean square
Many people have been familiar with such a historical figure as Pythagoras since school. The Pythagorean theorem and other discoveries named after the great mathematician are, of course, well-known, but they are not truly exciting discoveries. One of the most interesting and exciting discoveries can be called the Pythagorean square without remorse.
Slide 9
History of creation
Preserved historical sources indicate that the famous mathematician Pythagoras studied secret knowledge for a long time from the Egyptian priests. They say that in the Dagon tribe, fragments of the sciences of a previous civilization have been preserved. Possibly from Atlantis.
Slide 10
Pythagoras studied in Egypt and then brought to Europe digital matrices, previously known only to a narrow circle of select people. In an adapted version, the secret tables have survived to this day and are now known as the Pythagorean square. Pythagoras did not leave behind a collection of works; he kept his teachings secret and passed them on to his students orally. As a result, the secret died with them. Some information still leaked through the centuries, but now it is difficult to say how much of it is true and how much is false. Even with the Pythagorean theorem, not everything is certain. Some historians doubt the authorship of Pythagoras, arguing that it was widely used in the household by a variety of ancient peoples.
Slide 11
About the square
What does a Pythagorean square look like? This square consists of 9 cells, three in each row. They include processed data according to the date of birth of the person being studied. Why is such a well-known “square” needed? Since ancient times, each number has contained some information. So it is precisely on their meanings that all the fuss around a specific type of fortune telling is based. It would be more correct to say, not fortune-telling, but revealing the secrets of origin, current and even past lives.
Slide 12
Calculation of Pythagorean square
For example, Immanuel Kant April 22, 1724 We write: 04/22/1724. We add: 2+2+4+1+7+2+4=22. This is the first working number. Let's add its numbers again: 2+2=4. This is the Second Working Number. From the First Working Number we subtract double the first digit of your birthday: 22-4=18. This is the Third working number. For example, if the date of birth begins with 0 (01) – 0 is discarded, 1 is multiplied. We add the numbers of the Third working number: 1+8=9. The result is the Fourth working number.
Slide 13
We write your date of birth and four working numbers in a line: 2241724224189. Now let’s look at the table:
Slide 14
What does the data in the Pythagorean square determine?
First of all, it determines the character of a person and the amount of bioenergy in him, followed by the internal storage and level of health. Both the degree of down-to-earthness and the measure of talent become important indicators. Oddly enough, the above-mentioned square easily determines the sense of duty and level of intelligence.
Slide 15
Slide 16
Slide 17
What significant benefit can ordinary people derive from the information received from the Pythagorean square?
Description of the presentation by individual slides:
1 slide
Slide description:
Magic table of Pythagoras. https://aida.ucoz.ru Mathematics: in the world of interesting things. Author of the presentation: Blokhina E. V., teacher of the Municipal Educational Institution “Secondary School No. 2”, Cherkessk, 2013.
2 slide
Slide description:
The magic table of Pythagoras will help you decipher the code embedded in a person’s date of birth and find out your fate and the fate of people close to you. Fate according to Pythagoras. https://aida.ucoz.ru There is a theory that during his travels in Egypt, Pythagoras lived for a long time in the African Dogon tribe. This tribe, according to numerous legends and traditions, were not only contemporaries of the mysterious inhabitants of Atlantis, but also their diligent students. The Dogon believed that a person’s date of birth contained information about a person’s future, his character, health and other personality characteristics.
3 slide
Slide description:
https://aida.ucoz.ru The magic of Pythagorean numbers was not invented by the author, but was compiled from the numerological views of Egypt, Arabia, and Phenicia. According to his numerological view of things, the date of birth of a person is the starting point for calculating his basic qualities, the possible developments of his destiny and even the number of visits of the soul to earth.
4 slide
Slide description:
https://aida.ucoz.ru The Pythagorean table allows you to determine what nature rewards a person with at birth, what circumstances he will find himself in, and how his life will turn out. Pythagoras revered the number above all else; he believed that all people at birth receive their own number, which carries a certain characteristic. 1 Character (individuality) 4 Health (prosperity) 7 Talent (creativity) 2 Energy 5 Intuition 8 Responsibility (commitment) 3 Accuracy (precision) 6 Work attitude (groundedness) 9 Intelligence (mind)
5 slide
Slide description:
https://aida.ucoz.ru Let's look at everything using an example. First, we write down the date of birth of the person for whom we are making a forecast: 02/29/1996. Now we add the numbers of the day and month of birth: 2 + 9 + 2 = 13. Now we need to add the numbers of the year of birth: 1 + 9 + 9 + 6 = 25. We add the resulting numbers: 13 + 25 = 38, 38 is the first working number. We add up the digits of the first working number: 3 + 8 = 11, 11 is the second working number. From the first working number, subtract double the first digit of the birthday: 38 – 4 = 34, 34 is the third working number. Let's add the digits of the third working number: 3 + 4 = 7, 7 is the fourth working number.
6 slide
Slide description:
https://aida.ucoz.ru The first row of numbers is the date of birth: 29.2.1996. The second row is made up of working numbers: 38.11.34.7. Let's count the number of digits in two rows - 14. This means that man came to earth for the 14th time. Pythagoras said that after a person has lived 15 times (meaning the number of bodily incarnations or reincarnations), he can acquire enough qualities (positive or negative) to no longer return to earth, but to continue existing in higher or lower forms of life respectively.
7 slide
Slide description:
https://aida.ucoz.ru So, we draw a table, in each square of which we enter the same numbers from the two rows of numbers obtained earlier. Here's what happens: 1 111 4 4 7 7 2 22 5 - 8 8 3 33 6 6 9 999
8 slide
Slide description:
https://aida.ucoz.ru Data decryption occurs as follows. Square 1. Character (individuality). 1 – sophisticated egoist; 11 – close to selfishness; 111 – good character; stable; 1111 – very strong-willed, strong; 11111 – dictator, tyrant; 111111 – (rare) a person is cruel, but at the same time he can do the impossible for a loved one. It is very difficult with such a person.
Slide 9
Slide description:
https://aida.ucoz.ru Square 2. Energy. the absence of twos means the absence of bioenergy, which means that the bioenergy channel is open for an intensive gain of energy. These people love old things, treat others well, thereby trying to profit from others. Trained by nature. 2 – bioenergy is enough for life, but now, at this stage, it is not enough, so sports are required; 22 – enough bioenergy. You can already heal others. 222 – you are a good psychic; 2222 – these people are very much loved by the opposite sex. But if three sixes (666) are also added, beware of temptations.
10 slide
Slide description:
https://aida.ucoz.ru Square 3. Accuracy (accuracy). — there are no threes. This is a very neat and punctual person. Stands out among others with his conversation. 3 – these people are worried about disorder, but relatively (if I want, I do it, if I want, I don’t), it all depends on the mood; 33 – ability for science (wonderful mathematicians, physicists, chemists; 333 – ability for science (with a vengeance). Pedantry, accuracy, if there is no implementation in science. Square 4. Health (security). - absence of fours. This person is very sick 4 - will not be very sick, mainly due to old age; 44 - a very healthy person or has a high temperament; 444 - the same thing, only with doubled energy.
11 slide
Slide description:
https://aida.ucoz.ru Square 5. Intuition. - no A's. Unopened canal at birth. These people are always trying to do something, to do something, always in thought, in experiment, in calculations. Life experience shows that this person will make many mistakes. It's hard for these people to live. Everything that is given to them, they punch through with their heads; 5 – the channel is open, these people make fewer mistakes; 55 – highly developed intuition (investigators, lawyers); 555 – clairvoyant; everything that happens around them is clear to them. They know what they are doing; 5555 – clairvoyants; everything that is happening around them is clear to them. There are moments when they are on the other side of time and space.
12 slide
Slide description:
https://aida.ucoz.ru Square 6. Attitude to work (groundedness). - no sixes. A person came into this world to get a profession, physical labor is necessary, but he does not like it; 6 – grounded person. Physical labor is necessary. You can also think about studying; 66 – very grounded, but physical labor is not needed, and he loves it; 666 is an alarming sign. The person is very attractive, but also emotional. His partner should be with a large number of twos; 6666 - this person in his previous earthly transformations gained a lot of grounding and worked a lot. For this person there is no yoke of physical labor. He is always working. Such a person definitely needs to go to college, especially if there are also nines.
Slide 13
Slide description:
https://aida.ucoz.ru Square 7. Talent (creativity). - no sevens. This man was born to earn sevens in his subsequent transformations; 7 – a person lives much easier. There is talent, but not pronounced; 77 is a very strong sign, especially if its strength is fully developed. A musical man. Has artistic taste and can draw. If there are 1 and 2 in the calculation, then his egoism will guide him and his talent; no one needs him. A person walks on a razor's edge, endowed with everything - both good and bad. There will be no closed doors for him. If he is brought to justice, he will definitely be helped to win the case or pulled out of the debt trap. From childhood, you need to instill a sense of altruism. 777 is a special sign. These people will face serious difficulties; 7777 is a sign of alarm. People with this sign should be very careful.
Slide 14
Slide description:
https://aida.ucoz.ru Square 8. Responsibility (obligation). - absence of eights. A person will take something and is in no hurry to give it back; 8 – a person with a developed sense of responsibility; 88 – a very developed sense of responsibility, there is always a desire to help others; 888 is a sign of service to the people. Great responsibility. This is the sign of I. Gandhi; 8888 – this sign was only available in 1988. Children were born with developed abilities, with a penchant for studying the exact sciences. Square 9. Intelligence (mind). 9 – a person must develop another nine; 99 – born with a smart head, reluctant to learn; 999 - a person is smart by nature, everything is given to him; 9999 - the truth is revealed to a person in combination with a rare mind, but he is distinguished by rudeness and unmercifulness.
Municipal educational institution Komsomolskaya secondary school Pythagorean table Completed by: Baitsev Anton Petrovich, Completed by: Baitsev Anton Petrovich, 5th grade student, 5th grade student Leader: Elena Anatolyevna Baitseva, Supervisor: Elena Anatolyevna Baitseva, mathematics teacher mathematics teacher Komsomolsk, 2008
You will need numerical calculations every day, so the methods of their production must be learned first. A. N. Krylov You will need numerical calculations every day, so the methods of their production must be learned first. A. N. Krylov Purpose: to show easy, effective ways to memorize the Pythagorean table. Objectives: 1. Study the literature on this topic 2. Apply the acquired knowledge in practice 2. Apply the acquired knowledge in practice
Table of Pythagoras For the first time, the table of Pythagoras - approximately in the form in which we find it on the covers of student notebooks - appeared in the work of Nicomachus (Ι - ΙΙ century). For the first time, the Pythagorean table - approximately in the form in which we find it on the covers of student notebooks - appeared in the work of Nicomachus (Ι - ΙΙ century)
Pythagorean table (on fingers) Pythagorean table (on fingers) When initially learning to count, schoolchildren often resort to using their hands, and in further learning, in difficult cases, the same fingers help out: this is an invaluable visual aid.
Fingers help not only with counting and counting numbers within ten. You can quickly calculate examples from the multiplication table on your fingers, but only from 6 to 10. Let’s agree that the little finger on both the right hand and the left means the ring finger – 7, the middle finger – 8, the index finger – 9, and the thumb – 10. Let's agree that the little finger on both the right hand and the left means the ring finger - 7, the middle finger - 8, the index finger - 9, and the thumb - 10. Let us multiply 7 by 8. Bend two fingers (starting with the little finger) on one hand and 3 fingers on the other (corresponding to the numbers 7,8). Curled fingers correspond to the tens of the number, and free ones correspond to the units. To get tens, we add the number of bent fingers on one hand and on the other hand, and we get units by multiplying the number of free fingers on one and the other hand. Let us multiply 7 by 8. We bend two fingers (starting with the little finger) on one hand and 3 fingers on the other (corresponding to the numbers 7.8). Curled fingers correspond to the tens of the number, and free ones correspond to the units. To get tens, we add the number of bent fingers on one hand and on the other hand, and we get units by multiplying the number of free fingers on one and the other hand. In our example (7 · we had two fingers bent on one hand and three on the other. Two tens and three tens make five tens. There were three fingers free on one hand, and two on the other. Multiply: 3 · 2 = 6. thus, we get: = 56. In our example (7 · we had two fingers bent on one hand and three on the other. Two tens and three tens make five tens. There were three fingers free on one hand, and two on the other We multiply: 3 · 2 = 6. Thus, we get: = 56. To multiply 6 by 9, bend one finger on one hand, and four on the other. Add: = 5 (tens). Multiply: To multiply 6 by 9, on one hand we bend one finger, and on the other four. Add: = 5 (tens). Multiply: 1 · 4 = 4. We get: = · 4 = 4. We get: = 54. To multiply 6 by 6, by Bend one finger on one hand and on the other hand. Add: = 2 (ten). Multiply: To multiply 6 by 6, bend one finger on one and the other hand. Add: = 2 (ten). We multiply: 4 · 4 = 16. We get: = · 4 = 16. We get: = 36.
Patterns of the Pythagorean table for 9 Patterns of the Pythagorean table for 9 The first pattern. Let's multiply 9 by 2, as a result we get a number in which the tens are 1 less than the number by which we multiply 9; there should be so many units that the sum with the tens results in the number 9: 9 2 = 18 (2 dec. - 1 = 1 dec. , to this ten you need to add 8 units: 1 + 8 = 9) 9 2 = 18 (2 dec. - 1 = 1 dec., to this ten you need to add 8 units: 1 + 8 = 9) Multiply 9 by 3, it turns out 9 ·3=27 (3dec.-1=2dec., 2+7=9) Multiply 9 by 4, it turns out 9·4=36 (4dec.-1=3dec., 3+6=9) Multiply 9 by 5, it turns out 9·5=45 (5dec.-1=4dec., 4+5=9) Multiply 9 by 6, we get 9·6=54 (6dec.-1=5dec., 5+4=9) Multiply 9 by 7, it turns out 9·7=63 (7dec.-1=6dec., 6+3=9) Multiply 9 by 8, it turns out 9·8=72 (8dec.-1=7dec., 7+2=9) Multiply 9 by 9, it turns out 9·9=81 (9dec.-1=8dec., 8+1=9)
Second pattern Second pattern Let's multiply 9 by 2, as a result we get the following number: that the number by which we multiply 9, we turn into tens and subtract the same number of ones. Let's multiply 9 by 2, and as a result we get the following number: we turn the number by which we multiply 9 into tens and subtract the same number of ones. 9·2=18 (2·10-2=20-2) 9·3=27 (3·10-3=30-3) 9·4=36 (4·10-4=40-4) 9· 5=45 (5·10-5=50-5) 9·6=54 (6·10-6=60-6) 9·7=63 (7·10-7=70-7) 9·8= 72 (8·10-8=80-8) 9·9=81 (9·10-9=90-9) Patterns of the Pythagorean table for 9 Patterns of the Pythagorean table for 9
Multiplying by nine
There's some tricky stuff with the knuckles. Unfortunately, I don’t remember her.
We do this when multiplying by 9:
I hope everyone here knows that 2 x 10 is 20, 3 x 10 is 30, and 8 x 10 is 80?
Great?
So, multiplying by nine is multiplying by 10 minus a number.
That is:
2 x 9 is 20 – 2 = 18
A
5 x 9 is – 50 – 5 = 45.
And don’t forget that we actually already studied multiplication by two and by five and by three.
