Summary of OOD on FEMP on the topic “
Part and Whole” for children of the older group.
Educational area
: "Cognition."
Target:
Formation of the concepts of part and whole.
Educational objectives:
1. Strengthen the skills of forward and backward counting within 10.
2. Strengthen the ability to make a whole from parts.
3. Continue to form the idea that an object can be divided into two equal parts, learn to name the parts and compare the whole and the part.
4. Continue to introduce the division of a circle into 4 equal parts, learn to name the parts and compare the whole and the part.
Dividing a whole into parts of a task
Pedagogical experience suggests that without targeted training in dividing a whole into parts, preschoolers will not develop the concepts of “whole” and “part.” If you take a deeper interest in this topic, it will become clear that the process of familiarizing children with dividing a whole into parts in a preschool educational institution consists of three main tasks:
- Dividing a set into subsets;
- Practical division of objects into parts by folding, cutting, based on measurement, etc.
- Obtaining a whole from parts, i.e. establishing relationships between part and whole.
When solving the first problem - dividing a set into subsets - adults simply generalize the practical skills of children, helping them practically combine many objects into one whole and showing how this can be done. For example, collect 8 toys: 4 pyramids, 4 cars, put them in one box and make a generalization - “toys, only 8 pieces, take the pyramids,” then ask: “what is more: pyramids and cars combined or just pyramids? » In this case, the parts will be 4 pyramids and 4 cars. Each part is smaller than the whole, since there were 8 toys in the box, and there were 4 cars left. Almost all children know how to do this, but verbal conclusions must be taught and reinforced in practice in everyday life, play, and work.
Teaching children to divide into parts
Teaching preschoolers to divide a whole into parts almost always goes unnoticed, but they understand what they are required to do and internalize this requirement.
An example, in everyday life - you have a set of vegetables for a salad (many), ask your child to arrange the vegetables into groups (subsets): cucumbers, tomatoes, lettuce, etc. Ask your child to select from this set, for example, tomatoes that make up one part of the salad. Ask: “What is more than a tomato or other salad parts combined?” Next, state the conclusion - the vegetables for the salad are one whole, and the tomatoes are a part that should be put in the salad with other vegetables. In exactly this way, you can teach how to distinguish some dishes from the total quantity, pieces of furniture, work equipment, etc.
Dividing a whole into parts is a game like “collect a bouquet for your mother (grandmother, sister).”
Many flowers are one whole (bouquet), let your son or daughter single out, say, asters from this set. Conclusion: a bouquet is a “whole”, asters are a “part”. If the bouquet consists of one type of flower, then the flowers are distinguished by color. For example, select red ones from a bouquet of gladioli.
The bouquet is the “whole”, the red flowers are the “part”. A didactic game with dolls will help you solve all your problems. For example, the doll Natasha came to visit the doll Katya, and Katya only had one piece of cake (one apple, pear, pancake, etc.). What should you do to treat Natasha? The answer is obvious, and an adult will suggest the conclusion. Experience suggests that dolls must be selected to be of equal attractiveness. In the practice of kindergartens, there were cases when children divided pieces of different sizes and gave most of the treats to a doll that was more attractive in appearance.
The sequence of dividing a whole into parts
The practical sequential division of a whole into two parts occurs first, as a rule, using the example of geometric flat figures by folding them in half (2 equal parts), then the halves are divided in half, etc.
In this case, it is necessary to strictly ensure that children bend the shape correctly, placing one half on top of the other. The division process itself occurs by tearing the whole or cutting with a stationery knife or scissors. In this case, the adult needs to ensure that the form given to the child is divided equally. There is one more point that should be paid special attention to: children usually say not “in half”, but “in half”, and their parts often turn out not equal, but even, since they strive to do the work accurately and often trim off unevenness. Therefore, you should pay attention to the child’s speech and the correct use of mathematical terms. Exact science requires precise designation of the results of action. Various strips, ribbons, etc. are divided according to the same principle.
Next comes training in composing parts into a whole and emphasis is placed on the concepts of “whole” and “part.” At this stage, it is important to show children how a part relates to the whole: the part is less than the whole, and the whole is greater than the part. This is best learned in practice: children are given, say, 2 circles - one is divided into parts, and the other remains whole. By applying a part of a circle to the whole, we find out that the part is smaller than the whole and vice versa. When children understand the relationship between the whole and the part, they are asked to make a whole object into a circle (square, rectangle) from the parts, counting its parts. Together with adults, they learn and clarify that the number of parts varies; the more parts, the smaller the parts themselves. Later, offer the kids geometric mosaics, which, by the way, children love to play with. Please note that flat objects that cannot be bent. A piece of tape, a strip of paper of the required length, etc. can serve as a conditional measurement. If you have not divided the object into equal parts, then, by applying the parts to each other, clarify which part is larger and which is smaller and add these parts so as to get the whole object. The conclusion suggests itself - an object can be divided into unequal parts, but then it cannot be said that it is divided equally. We simply say: “We divided the circle into 2 (4,8) parts.”
Question: What does this knowledge give to preschool children? Is it necessary to give the concepts of whole and part? Yes, it is necessary. Teaching children to divide a whole into parts allows them to see the relationship between the whole and the part and learn the pattern in things and phenomena that are hidden for the direct perception of objects (looking at a square, we don’t think that it can be divided, and having divided a square, we perceive it already according to -to another). In addition, knowledge of the relationships between the whole and the part contributes to the formation of logical thinking, the ability to find causal relationships, and judge the initial data based on the results. In a word, it will have a broad general developmental effect.
Dividing a whole into parts using a piece of paper
We will need several sheets of paper and scissors.
First you need to show the child a piece of paper and explain that it is a whole object. Then you should fold the paper in half, we get half a sheet.
Having unfolded the sheet, you need to explain to the child that two halves of the sheet make up one whole sheet, and the same happens with any other object. It is necessary to show that the two halves are absolutely identical, equal parts.
Now fold the sheet in half again, that is, divide the sheet into quarters. So the child needs to be shown that four equal parts also make up one whole sheet of paper. With the help of such manipulations, a child can be taught to divide an object into equal parts, that is, in half.
Next, you should explain to the child that when dividing, equal parts are not always obtained. To do this, you need to bend a sheet of paper in an arbitrary place. But even in this case, the two resulting parts form one whole.
And only after the child has mastered dividing into parts by bending can the scissors be used. After cutting a sheet of paper in half, you need to show the child that the resulting two parts make up a whole sheet. Then you can cut these halves in half again and invite the child to make a sheet of paper from four small parts.
Then you need to take another sheet and cut it randomly into several parts. Thus, the child will see that it is possible to divide into unequal parts.
An important area in preparing preschoolers for computing activities is dividing the whole into parts. Children repeatedly encounter the need to divide a set, as well as a separate object, into parts in everyday life, during games. So, more than once they had to share toys, sweets (sweets, cookies) among themselves, buy part (half, quarter) of bread in the store, divide the beds into separate areas, etc.
Dividing a whole object or set into several equal parts makes it possible to understand a number of patterns in things and phenomena, promotes the formation of logical thinking, the development of the ability to find cause-and-effect relationships, allows one to draw a conclusion about the initial data based on the results of the work, etc.
Although children very early on practically divided a set into parts (individual elements), and also performed the opposite actions - from individual elements (parts) they created a whole set, they were only given the task of determining the number of elements (actually parts) in this set and were not considered, but that is why the relationship of the part to the whole was not realized.
Later, when familiarizing children with the quantitative composition of the numbers of the first ten, the main attention was paid to the children’s understanding of the relationship of the unit (as a part) to the number (as a whole).
However, pedagogical experience shows that without purposeful training in dividing into parts, children do not form clear ideas about the whole and its parts, about the relationships of the part to the whole, about the connections between parts (equal and unequal), etc.
The process of familiarizing children with dividing a whole into parts consists of the following components: dividing a set into subsets, practical dividing an object into parts by folding, cutting, based on measurement and obtaining a whole from parts, i.e. establishing relationships between a part and a whole. First, the teacher shows the children that sets can be homogeneous and heterogeneous, consisting of two or three parts. These parts can be combined. For example, children perceive and count bunnies and bears as two independent sets (two aggregates, groups). “How many bunnies? How many bears? What more? Less of what? How can you call both bunnies and bears in one word? That's right, these are toys." So, the teacher leads the children to the fact that the number of individual small sets can be combined into one large set. This last set is called the whole, and the primary (small) sets are called parts of this whole. The whole is always greater than any of its parts (even the largest).
DIVIDING THE WHOLE INTO PARTS
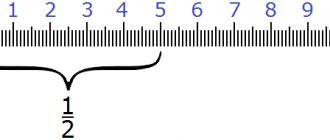
Further development of the concept of number is provided by exercises in dividing objects into equal parts.
Children learn to see parts in a whole object, identify the relationship between the whole and the part. 6-7 (sequentially conducted) lessons are devoted to dividing subjects into equal parts, and then they periodically return to this until the end of the year. In the first lesson, situations are created in which it becomes necessary to divide an object into 2 equal parts, for example, divide a treat between 2 dolls or 2 children (guests), help 2 greedy bear cubs divide cheese, etc. The teacher shows how to divide objects into 2 equal parts, i.e. in half, emphasizes that he precisely folds and cuts the object in the middle, then compares the resulting parts, placing one on top of the other or applying one to the other. Children count the parts and make sure they are equal. The teacher says that any of 2 equal parts is usually called a half. The teacher deliberately divides the next subject into 2 unequal parts and asks: “Can such a part be called half? Why not?" Children see that objects can be divided into both equal and unequal parts. One of 2 parts can be called half only when the parts are equal. Gradually, children become convinced of how important it is to accurately fold and cut objects so that equal parts are obtained. Having completed the action, they check (by superimposition and application) whether the parts are equal, count them and, joining together, get a whole object, trace its outline and parts with their hand, compare the size of the whole and the parts. In the second lesson, the teacher expands the range of objects that the children divide in half. You can use cereal and water. They are distributed equally into 2 transparent glasses of the same size. In the third lesson they show how to divide objects into 4 equal parts, i.e. in half and in half again. Establish relationships between the whole. and by part: the part is less than the whole, the whole is greater than the part. If many new children have entered the preparatory school group, it is advisable to start by dividing objects into parts by folding. Children receive 2 objects of the same size, which they are convinced of by placing 1 object on top of another. They divide 1 object into 2 equal parts, the other into 4. By connecting the parts together, they get the whole object, count the parts, show 1 of 2 parts, 2 of 2 parts, respectively 1 (2, 3, 4) of 4 equal parts . Compare the size of 1 part and the whole. Similarly, the next lesson shows the relationships between different parts of a single whole. Children receive 3-4 sheets of paper of the same size, place the first one in front of them, divide the second into 2 equal parts, and the third into 4 (the fourth sheet can be divided into 8 equal parts). Connecting the parts (as if leaving the sheets whole), children lay them out one under the other, show 1 of 2 parts, 1 of 4 parts, compare the size of 1/2 and 1/4 parts and their quantity. Which is smaller: a whole sheet or half? What is more: half or 1 of 4 parts, 1/4? Which part is the smallest? Why? Etc. It is useful to establish a connection between the number of cutting actions and the number of resulting parts. For example, the teacher asks: “How many times do you need to fold the square in half to get 2 equal parts? What about 4 parts? To generalize knowledge, you can use schemes for dividing an object into equal parts (apple, circle, square, etc.). Looking at the diagram with the children, the teacher asks: “How many equal parts did you first divide the apple into?” How many of these parts did you get? How many equal parts was the apple then divided into? How many parts did you get? What is more and what is less: half or a whole apple? 2 halves or a whole apple? 1 of 4 parts (1/4) or half (1/2)?” Etc. Children usually perceive such exercises as a game and answer questions with pleasure. In subsequent classes, exercises are carried out in dividing geometric figures into 2, 4, 8 parts and in composing whole figures from parts, for example: “How should you fold and cut a square to make 2 equal rectangles? To make 2 equal triangles? (You need to bend the square side to side or fold a corner with a corner.) Children talk about what shapes and how they divided and what happened as a result of division, what shape the parts are, how many there are. They also conduct special exercises in composing figures from parts: “How many circles can be made from 4 semicircles?” You can show the parts of the figures: “This is 1 of 4 (1 of 2, 4 of the parts of the square. Guess how many squares there were. Make them.” It is useful to encourage children to find the most convenient (rational) ways of dividing objects into parts, taking into account their size, shape , proportions. For example, you need to compare how easier it is to divide a narrow strip (ribbon) and a square (piece of fabric) into 4 parts. Children decide that it is more convenient to fold a narrow strip in half lengthwise and in half again, and to fold a square sequentially with opposite sides. At one of the last lessons on this topic, it is advisable to compare the results of dividing objects of different sizes into equal parts. Children are presented with 2 objects of contrasting sizes, for example, a large and small circle or square. The teacher divides the figures into 2 (4) equal parts, takes 1 of the parts each figure and asks the children to say what these parts can be called (“Half, 1 of 2 parts, 1/2.”) “This is half and this is half. Explain why they are different sizes.” Helping the children, the teacher shows spare figures of the corresponding size. Concludes: half of the large circle is greater than half of the small one, and half of the small circle is less than half of the large circle. The objects were of different sizes, and their parts were also of different sizes. It is advisable here to contrast the results of dividing objects of equal size into parts. When conducting exercises in dividing objects into equal parts, the teacher constantly makes sure that children accurately perform actions, check the equality of parts, using the techniques of superimposition and application, as well as measuring with a conventional measure, teaches children to use the following words and expressions in speech: divide into equal parts, whole, half, halves, one of two parts, one of four parts, and a little later - one second, one fourth. The last expressions should not be specially memorized; children gradually remember them. Each time the guys count the parts, and by connecting them together, they get 1 whole object, establish the relationship between the whole and the part. As a result of a series of activities, you can ask children questions that allow them to generalize their knowledge: “How many times do you need to fold a circle to divide it into 2 (4, equal parts? If you fold a square in half 1 (2, 3) times, how many parts will you get? If I I ask you to give me half a pear, how many parts will you divide it into? And if I ask for 1/4? How many such parts are in a whole pear? How many parts have I divided the whole into if it is 1 part out of 4 (out of 2)? If we divide a large one in half object and small, half of which object will be larger? And smaller? Why?" Division into parts will allow children to show the possibility of splitting objects into equal shares, to clearly identify the relationship between the whole and the part, and thus creates a condition for children to understand the process of measuring quantities. When measuring, an object is, as it were, split into parts, the sum of which characterizes its size.After children master the techniques of measurement, they can be asked to divide a stick, a rod, a plank, a rectangle drawn on a board, etc. into 2, 4, 8 equal parts. The guys see that these objects cannot be bent, and the learned methods of division are not suitable. What should I do? The teacher is in no hurry to give a hint. He places objects in front of the children that can be used as measurements. This is where children are helped by understanding the relationship between the size of objects and the size of their corresponding parts. 1-2 leading questions and the children guess that they need to choose a suitable measure, measure out a piece equal to the length of the object, divide the measure (fold) into the appropriate number of parts and then measure these parts on the object, make marks with a pencil, chalk, etc. It is useful to exercise the children in dividing geometric shapes drawn on checkered paper. Children draw figures of a given size, and then, as directed by the teacher, divide them into 2 or 4 equal parts, measuring by square. According to the instructions of the teacher, they draw segments of length from 2 to 10 cells from top to bottom or from left to right and divide them into parts equal to the length of 1, 2, 3, 4, 5 cells. They establish connections between the size of the measure and the number of resulting parts: “How many parts will the segment be divided into if each part is equal to 2 cells? If we divide a segment into 3 equal parts, what will 1 part be equal to?” Exercises in dividing objects into equal parts allow you to move on to learning to measure, and the ability to measure makes it possible to divide a wide variety of objects into parts.
Dividing a whole into parts using a ribbon
In fact, you can use not only ribbon, but also just a paper strip. In addition, you will need toys. There must be an even number of them. These can be soft toys or dolls. The goal of the game is to divide the ribbon equally among everyone.
For example, if we have 4 dolls at our disposal, then the ribbon or strip needs to be divided into 4 parts. To do this, you need to divide the dolls first into 2 groups, and then each of the groups in half again. The ribbon is divided in the same way. So, the child will learn to divide several objects into equal parts.
You can and should consolidate the material you have covered day after day. For example, when a child helps set the table and cut the cake for tea. The acquired skills are also applicable in games. So, when playing with a construction set or putting together puzzles, you can remind your child that he is making a whole object out of small parts.
A technique for teaching dividing a whole into equal parts.
In Art. gr. – in the 1st-2nd quarter we teach dividing a whole into parts, in the 3rd – we practice. Dividing the whole into parts is the basis for the formation of logical thinking and ingenuity. The process of familiarizing yourself with dividing a whole into parts consists of several stages: 1. dividing a set into subsets.
2. dividing a whole into parts using the bending technique.
3.using the technique of cutting (tearing).
4. establishing relationships between parts and the whole and parts among themselves.
Stage 1: First, the teacher shows that sets consist of 2-3 parts and these parts can be combined into one large whole. The whole is always greater than any of its parts and vice versa.
Stage 2: Quantitative relationships are established between the whole and the parts. Folding: first we divide the strip into 2 equal parts, then into 4. We introduce the terms “half”, “quarter”.
Stage 3: 3 strips are used simultaneously: the 1st is a control strip, the 2nd is divided into 2 equal parts, the 3rd into 4 parts. First they use strips of paper, later - geometric shapes, real objects. When it is impossible to bend an object, we divide the whole into parts using a conventional unit (example: bend a cord equal to the side of the rectangle by 2, then by 4. Set aside on the side of the rectangle and make notes).
Methodology for introducing preschoolers to the size of objects.
In 2 ml. gr. 2 objects are used, the compared property of which is clearly expressed. In the first lessons, they use flat objects, constantly expanding their range, and increasing the number of colors. First they teach to show and name the length, then other measurements. The starting point of the work is an examination. When showing length, the hand moves from left to right, width - across the object, height - from bottom to top or top to bottom, thickness - by spreading the fingers. The thickness of round objects is determined by girth. Show - 2-3 times. Use application and overlay. On Wednesday. gr. compare 3-5 objects that differ less in size. Children learn a comparative assessment of magnitude (longer, shorter, shortest) and establish mutually formative relationships. First, they teach how to arrange objects in order in a row, using a model, then according to the rules (starting with the longest). The selection rules (each time choosing the longest one out of all) determines the sequence of actions. Checking for correctness - comparing objects with those next to them in a row. Comparing flat objects by length and width at the same time. Next they move on to the three dimensions of an object (determining length, width, height). In the older group there are 10 subjects with an even smaller difference. The same objects are placed in a row, either by one or by a second characteristic. The object indicated by the teacher is compared not only with the neighboring one, but also with the others. Afterwards they are taught to use a conventional measure.
Methods of introducing preschool children to the elements of mathematics in different age groups.
FEMP classes are structured taking into account general didactic principles: scientific, systematic, accessible, visual, consistent, individual approach. In all age groups, classes are conducted frontally or in subgroups. Classes are held once a week. With age, the length of the lesson increases. New knowledge is given in small parts, so the overall program task is usually divided into a number of small ones and sequentially implemented over several lessons. In the practice of FEMP work, the following types of classes have developed: in the form of a didactic game, in the form of didactic exercises, in the form of a didactic lesson. games and exercises In the process of organizing various types of activities, children must master a certain number of learning skills. The amount of knowledge by age is determined by the Praleska program.
Development of issues of familiarization with mathematical concepts in the works of foreign teachers.
In modern foreign work on FEMP of preschoolers, much attention is paid to the pre-numerical period. M, Fiedler (Poland) and E. Doom (Germany) attach great importance to the formation of the idea of numbers in the process of practical actions with many objects. The formation of quantitative, spatial and temporal concepts in children is interconnected. R. Green, V. Lacson (USA) show how, under the influence of comparison of two or several sets, children form an idea of the place of a number among other numbers in the natural series. They propose to form mathematical concepts taking into account a variety of impressions. Much attention was paid to applying the acquired knowledge in practice. Fr. Teachers distinguish three types of mathematical activity in mother schools: classification, similarity, and the formation of concepts of space and time. We have developed a system of logic games for children of different ages.
