Only the lazy do not say that the school curriculum today is difficult and there is an exorbitant amount of homework. Children, they say, do not have time to attend clubs and sections, they damage their eyesight by poring over textbooks and notebooks - they gain knowledge that will not be useful in life.
We decided to check what the problem is with modern secondary education. Maybe today's children are much stupider than previous generations? Or do teachers assign homework not just one or two exercises or paragraphs, but half a chapter at once? Or are textbooks that meet federal state standards difficult to write and do not provide the necessary knowledge on the subject?
Let's conduct an experiment. I, the mother of a sixth-grader with a higher education in the humanities, will do my homework for one of the days. It was received by students of a regular secondary school.
We complete the lessons assigned for Wednesday. Photo: AiF/ Nadezhda Uvarova
SanPINs cover everything
The time that a student can spend on homework is fixed by law. Along with the standards for ventilation of premises and the location of the blackboard in the classroom, it is reflected in the “Sanitary and epidemiological requirements for the conditions and organization of training in educational institutions,” signed by the chief sanitary doctor of Russia at that time, Gennady Onishchenko . The document states that it is permissible for a sixth-grader to spend 2.5 hours a day on homework. And for a student in grades 2-3, for example, no more than 1.5 hours. The same standards also highlight the scale of subject difficulty for each year of study. They regulate how subjects should be scheduled so that the load is distributed evenly. For the purity of the experiment, let's take one of the most difficult days - Wednesday. It is recommended to place the most difficult subjects in the middle of the week. There are six lessons on the schedule. I have to learn English, mathematics, Russian, literature and history. Music doesn't count: they didn't ask.
Work program for the mathematics curriculum for grade 6
Explanatory note
The work program is drawn up in accordance with the following regulatory legal acts:
- Law of the Russian Federation “On Education in the Russian Federation” (dated December 29, 2012 No. 273-FZ);
- Federal State Educational Standard LLC (order of the Ministry of Education and Science of the Russian Federation dated December 17, 2010 No. 1897);
- Order of the Ministry of Education and Science dated December 31, 2015 No. 1577 “On amendments to the federal state educational standard of basic general education, approved by order of the Ministry of Education and Science of the Russian Federation dated December 17, 2010 N 1897”;
- Federal list of textbooks (2019);
- Sample Basic Educational Program of LLC;
- Regulations on the procedure for developing and approving work programs for academic subjects at the Dubrovskaya secondary school;
- Curriculum of the MBOU Dubrovskaya secondary school for the 2019-2020 academic year.
Educational complex "Mathematics" for 6th grade:
— Textbook “Mathematics” 6th grade.
Authors:
Nikolsky S.M., Potapov M.K., Reshetnikov N.N., Shevkin A.V., Andrianov V.A.
- Workbook. 6th grade. Authors:
Potapov M.K., Shevkin A.V. - Didactic materials.
6th grade. Authors:
Potapov M.K., Shevkin A.V. - Thematic tests.
6th grade. Authors:
Chulkov P.V., Shershnev E.F., Zarapina O.F. - Textbook “Tasks for ingenuity.”
5-6 grades. Authors:
Sharygin I.F., Shevkin A.V. - A book for teachers.
5-6 grades. Authors:
Potapov M.K., Shevkin A.V.
The study of mathematics in 6th grade is aimed at achieving the following goals:
- master the system of mathematical knowledge and skills necessary for application in practical activities, studying related disciplines, and continuing education.
Tasks:
- to form intellectual development, interest in the subject “mathematics”, personality traits necessary for a person to live a full life in modern society, characteristic of mathematical activity: clarity and accuracy of thought, criticality of thinking, intuition, logical thinking, elements of algorithmic culture, spatial concepts, ability to overcome difficulties;
- to form an understanding of the ideas and methods of mathematics as a universal language of science and technology, a means of modeling phenomena and processes;
- to cultivate a culture of personality, an attitude towards mathematics as a part of universal human culture, which plays a special role in social development.
In the course of teaching mathematics in the 6th grade, working on developing in students the knowledge and skills listed in the program, attention should be paid to ensuring that they master general educational skills, a variety of methods of activity, and gain experience:
- planning and implementation of algorithmic activities, execution of specified and construction of new algorithms;
- solving various classes of problems from various sections of the course, including problems that require finding ways and methods of solution;
- research activities, development of ideas, conducting experiments, generalization, setting and formulating new problems;
- clear, accurate, competent presentation of one’s thoughts in oral and written speech, the use of various languages of mathematics (verbal, symbolic, graphic), free transition from one language to another for illustration, interpretation, argumentation and proof;
- conducting evidence-based reasoning, argumentation, putting forward hypotheses and their justification;
- searching, systematizing, analyzing and classifying information, using a variety of information sources, including educational and reference literature, modern information technologies.
The set goals are achieved through the use of various forms of work (individual, group, frontal), the use of electronic testing and a simulator helps to consolidate educational skills, helps to monitor and self-monitor educational achievements.
General characteristics of the subject
The content of mathematics education in relation to primary school is presented in the form of the following substantive sections. This is arithmetic; algebra; functions; probability and statistics; geometry. Along with this, the content of basic general education includes two additional methodological sections: logic and sets; mathematics in historical development, which is associated with the implementation of the goals of general intellectual and general cultural development of students. The content of each of these sections unfolds into a content-methodological line that permeates all the main sections of the content of mathematical education at a given stage of education. At the same time, the first line - “Logic and sets” - serves the purpose of students mastering some elements of the universal mathematical language, the second - “Mathematics in historical development” - contributes to the creation of a general cultural, humanitarian background for studying the course.
The content of the “Arithmetic” section serves as the basis for students’ further study of mathematics, contributes to the development of their logical thinking, the formation of the ability to use algorithms, as well as the acquisition of practical skills necessary in everyday life. The development of the concept of number in basic school is associated with rational and irrational numbers, the formation of primary ideas about the real number. Completion of the number line (systematization of information about real numbers, complex numbers), as well as more complex questions of arithmetic (Euclidean algorithm, the fundamental theorem of arithmetic), is assigned to the level of general secondary (complete) education.
The content of the “Algebra” section helps students develop a mathematical apparatus for solving problems from different branches of mathematics, related subjects, and the surrounding reality. The language of algebra emphasizes the importance of mathematics as a language for constructing mathematical models of processes and phenomena in the real world. The objectives of studying algebra also include the development of algorithmic thinking, which is necessary, in particular, for mastering a computer science course, and mastering the skills of deductive reasoning. The transformation of symbolic forms makes a specific contribution to the development of students’ imagination and their abilities for mathematical creativity. In the basic school, the material is grouped around rational expressions, and questions related to irrational expressions, trigonometric functions and transformations are included in the content of the mathematics course at the senior level of school.
The content of the “Functions” section is aimed at students gaining specific knowledge about function as the most important mathematical model for describing and studying various processes. The study of this material contributes to the development of students' ability to use various languages of mathematics (verbal, symbolic, graphic), and contributes to the formation of ideas about the role of mathematics in the development of civilization and culture.
The section “Probability and Statistics” is a mandatory component of school education, enhancing its applied and practical significance. This material is necessary, first of all, for the development of functional literacy in students - the ability to perceive and critically analyze information presented in various forms, understand the probabilistic nature of many real dependencies, and make simple probabilistic calculations. Studying the basics of combinatorics will allow the student to consider cases, enumerate and count the number of options, including in the simplest applied problems.
When studying statistics and probability, ideas about the modern picture of the world and methods of its research are enriched, an understanding of the role of statistics as a source of socially significant information is formed, and the foundations of probabilistic thinking are laid.
The purpose of the content of the “Geometry” section is to develop students’ spatial imagination and logical thinking by systematically studying the properties of geometric figures on a plane and in space and applying these properties when solving problems of a computational and constructive nature. A significant role in this is given to the development of geometric intuition. The combination of clarity and rigor is an integral part of geometric knowledge. The material related to the “Coordinates” and “Vectors” blocks largely carries interdisciplinary knowledge that is used both in various mathematical disciplines and in related subjects.
A special feature of the section “Logic and Sets” is that the material presented in it is mainly studied when considering various issues of the course. The corresponding material is aimed at the mathematical development of students, developing their ability to accurately, concisely and clearly express thoughts in oral and written speech.
The section “Mathematics in Historical Development” is intended to form ideas about mathematics as part of human culture, for the general development of schoolchildren, and to create a cultural and historical learning environment. There are no special lessons allocated for it, its assimilation is not controlled, but the content of this section is organically present in the educational process as a kind of humanitarian background when considering the issues of the main content of mathematical education.
Place of the subject in the curriculum
According to the basic curriculum for general education organizations of the Bryansk region for the 2019-2020 academic year and the curriculum of the Dubrovskaya secondary school for 2019-2020. are allocated for studying mathematics in the 6th grade at the rate of 5 hours per week
.
Scheduled control work
within a year 9.
Planned results of mastering the course
Personal results
Personal universal learning activities
Within the cognitive component
will be formed:
- ideas about facts illustrating important stages in the development of mathematics (the invention of decimal numbering, ancient systems of recording numbers, ancient systems of measures; the origin of geometry from the practical needs of people);
- orientation in the system of requirements for teaching mathematics.
Within the framework of value and emotional components
will be formed:
- positive, emotional perception of mathematical objects, reasoning, tasks, problems under consideration.
Within the framework of the activity (behavioral) component
will be formed:
- readiness and ability to fulfill the norms and requirements presented in mathematics lessons.
The student will have the opportunity to form:
- expressed stable educational and cognitive motivation and interest in studying mathematics;
- the ability to choose the desired level of mathematical results;
- adequate positive self-esteem and self-concept.
Meta-subject educational results
Regulatory universal learning activities
The student will learn:
- joint goal setting with the teacher in mathematics lessons and in mathematical activities;
- analyze the conditions of the task (for new material - based on taking into account the action guidelines identified by the teacher);
- act in accordance with the proposed algorithm, create simple algorithms for calculations and constructions;
- apply self-control techniques when solving mathematical problems;
- evaluate the correctness of the action and make the necessary adjustments based on existing templates.
The student will have the opportunity to learn:
- independently set educational goals;
- see different strategies for solving problems, consciously choose a solution method;
- the basics of self-regulation in mathematical activity in the form of conscious management of one’s behavior and activities aimed at achieving goals.
Communicative universal learning activities
The student will learn:
- build speech structures using studied terminology and symbols, understand the meaning of the task, translate from natural language into mathematical language and vice versa;
- exercise control, correction, assessment of the partner’s actions, and be able to persuade.
The student will have the opportunity to learn:
- take the initiative in solving a given task;
- ask questions necessary to organize your own activities of interaction with others;
- establish and compare different points of view before making decisions and choices;
- o display in speech (description, explanation) the content of the actions performed.
Cognitive universal learning activities
The student will learn:
- the basics of implementing design and research activities under the guidance of a teacher (with the help of parents);
- search the educational text and additional sources for answers to the questions posed; highlight semantic fragments in it;
- analyze and comprehend the texts of problems, reformulate their conditions, model the condition using diagrams, drawings, tables, real objects, build a logical chain of reasoning;
- formulate the simplest properties of the mathematical objects being studied;
- with the help of the teacher, analyze, systematize, and classify the mathematical objects being studied.
The student will have the opportunity to learn:
- select the most effective ways to solve problems depending on specific conditions;
- independently define concepts;
- build the simplest classifications based on dichotomous division (based on negation).
Subject educational results
Fractions. Rational numbers
The student will learn:
- operate at a basic level with the concepts: natural number, integer, common fraction, mixed number, decimal fraction, rational number;
- use the properties of numbers and rules for operating with them when performing calculations;
- perform calculations with rational numbers, combining oral and written calculation methods, use a calculator to use the acquired skill in related disciplines (chemistry, physics, etc.);
- use concepts and skills related to the proportionality of quantities, percentages, while solving mathematical problems and problems from related subjects, perform simple practical calculations;
- use the learned concepts and skills while solving mathematical problems and problems from related subjects, perform simple practical calculations;
- move from one form of writing numbers to another;
- compare rational numbers.
The student will have the opportunity to:
- learn to use techniques that rationalize
calculations, acquire the habit of controlling calculations, choosing the method appropriate for the situation.
Approximations and estimates
The student will learn:
- use elementary concepts associated with approximate values of quantities when solving problems;
- estimate and evaluate the meanings of numerical and letter expressions.
The student will have the opportunity to:
- understand that the numerical data that is used to characterize objects in the surrounding world are predominantly approximate, that by recording
the approximate values contained in information sources, one can judge the approximation error; - understand that the error in the calculation result
must be commensurate with the error in the original data.
Geometric figures
The student will learn:
- Operate at a basic level with the following concepts: figure, point, segment, straight line, ray, broken line, angle, polygon, triangle and quadrangle, rectangle and square, circle and circle, cuboid, cube, ball. Draw the studied figures by hand and using a ruler and compass.
In everyday life and when studying other subjects:
- solve practical problems using the simplest properties of shapes.
The student will have the opportunity to:
- extract, interpret and transform information about geometric shapes presented in drawings;
- draw the studied figures by hand and using computer tools.
Measurements and calculations
The student will learn:
- measure lengths, distances, angles using tools for measuring lengths and angles;
- calculate the area of rectangles and squares.
In everyday life and when studying other subjects:
- calculate distances on the ground in standard situations, the area of rectangles;
- perform simple constructions and measurements on the ground necessary in real life.
The student will have the opportunity to:
- measure lengths, distances, angles using tools for measuring lengths and angles;
- calculate the surface areas of rectangular parallelepipeds, cubes, volumes of rectangular parallelepipeds, cubes.
In everyday life and when studying other subjects:
- calculate the area of rectangular plots and the volume of rooms;
- carry out constructions on the ground necessary in real life;
- estimate the sizes of real objects in the surrounding world.
Word problems
The student will learn:
- solve simple plot problems of various types involving all arithmetic operations;
- build a model of the problem conditions (in the form of a table, diagram, drawing), which gives the values of two of the three interrelated quantities, in order to find a solution to the problem;
- implement a method of searching for a solution to a problem in which reasoning is built from condition to requirement or from requirement to condition;
- draw up a plan for solving the problem;
- highlight the stages of solving a problem;
- interpret the computational results in the problem, examine the resulting solution to the problem;
- know the difference in the speed of an object in still water, against the current and along the flow of the river;
- solve simple problems of finding a part of a number and a number from its part;
- solve the simplest problems of different types (work, shopping, movement) connecting three quantities, highlight these quantities and the relationships between them;
- solve simple problems into parts;
- solve simple logical problems using reasoning.
In everyday life and when studying other subjects:
- put forward hypotheses about possible limiting values of the sought quantities in the problem (make estimates)
The student will have the opportunity to:
- solve simple and complex problems of various types, as well as problems of increased difficulty;
- use different short notes as models of texts of complex problems to build a search scheme and solve problems;
- know and apply both ways of finding solutions to problems (from requirement to condition and from condition to requirement);
- simulate reasoning when searching for solutions to problems using a graph diagram;
- highlight the stages of solving the problem and the content of each stage;
- interpret the computational results in the problem, examine the resulting solution to the problem;
- analyze all possible situations of the relative position of two objects and changes in their characteristics during joint movement (speed, time, distance) when solving problems on the movement of two objects both in one and in opposite directions;
- explore all sorts of situations when solving problems involving movement along a river, consider different frames of reference;
- solve various problems “in parts”,
- solve and justify your solution to problems (highlight the mathematical basis) for finding a part of a number and a number by its part based on the specific meaning of the fraction;
- realize and explain the identity of tasks of different types that connect three quantities (work, shopping, movement); identify these quantities and the relationships between them, apply them when solving problems, and construct your own problems of these types.
In everyday life and when studying other subjects:
- when solving problems, highlight the characteristics of the situation considered in the problem that are different from the real ones (those from which we have abstracted), construct new situations taking into account these characteristics, in particular, when solving problems on concentration, take into account the density of the substance;
- solve and construct problems based on consideration of real situations in which an exact computational result is not required;
- solve problems involving movement along a river, considering different frames of reference.
Algebraic expressions. Equations.
The student will learn:
- solve problems containing letter data, work with formulas;
- solve the simplest equations based on dependencies between the components of arithmetic operations;
- build points and figures on the coordinate plane according to given coordinates, determine the coordinates of points.
- understand the equation as the most important mathematical model for describing and studying a variety of real situations, solve word problems using the algebraic method;
The student will have the opportunity
- master special techniques for solving equations and systems of equations; confidently apply the apparatus of equations to solve a variety of problems in mathematics, related subjects, and practice;
Descriptive statistics.
The student will learn:
- Present data in the form of tables, charts,
- read information presented in the form of a table or diagram.
- use the simplest ways to present and analyze statistical data.
The student will have the opportunity to:
- operate with concepts: bar and pie charts, data tables, arithmetic average,
- extract information presented in tables and diagrams;
- make tables, build diagrams based on data.
- acquire initial experience in organizing data collection when conducting
a public opinion survey, analyze them, present the survey results in the form of a table or diagram.
In everyday life and when studying other subjects:
- extract, interpret and transform information presented in tables and diagrams, reflecting the properties and characteristics of real processes and phenomena.
Random events and probability. Combinatorics
The student will learn
- find the probability of a random event.
- solve combinatorial problems of finding the number of objects or combinations by enumerating options.
The student will have the opportunity
- learn some
special techniques for solving combinatorial problems.
History of mathematics
The student will learn:
- describe individual outstanding results obtained in the development of mathematics as a science;
- know examples of mathematical discoveries and their authors, in connection with domestic and world history.
The student will have the opportunity to:
- Characterize the contribution of outstanding mathematicians to the development of mathematics and other scientific fields.
Educational, methodological and logistical support of the educational process
Educational and methodological kit:
1) Mathematics: 6th grade: textbook for students of general education institutions / S.M.Nikolsky, M.K.Potapov, N.N.Reshetnikov, A.V.Shevkin. – M.: Education, 2013
2) Mathematics: 6th grade. Workbook. Part 1/ M.K.Potapov, A.V.Shevkin. – M.: Education, 2014
3) Mathematics: 6th grade. Workbook. Part 2/ M.K.Potapov, A.V.Shevkin. – M.: Education, 2014
4) Mathematics: 6th grade. Didactic materials / M.K.Potapov, A.V.Shevkin. – M.: Education, 2013
5) Mathematics. Thematic tests. 6th grade / P.V. Chulkov, E.F. Shershnev, O.F. Zarapina - M.: Education, 2013
6) Mathematics. Guidelines. 6th grade: a manual for teachers of general education. institutions / M.K. Potapov, A.V. Shevkin. - M.: Education, 2014.
Additional literature:
1) Chesnokov A.S. Didactic materials in mathematics for grade 6 / A.S. Chesnokov, K.I. Neshkov. - M.: Classic Style, 2012.
2) Ershova A.P., Goloborodko V.V. Independent and test work in mathematics for grade 6. - M.: Ilexa, 2014.
3) Minaeva S.S. 20 tests in mathematics: grades 5-6.-M.: Publishing House “Exam”, 2013
4) Entertaining tasks in teaching mathematics [Text]/M. Yu. Shuba. - M.: Education, 1994. - 124 p.
5) Tasks for ingenuity. Grades 5-6: a manual for students of general education institutions / I.F. Sharygin, A.V. Shevkin. – M.: Education, 2010
Internet resources:
1) I’m going to a mathematics lesson (methodological developments). - Access mode: www.festival.1september.ru
2) Lessons, notes. – Access mode: www.pedsovet.ru
3) A unified collection of educational resources. — Access mode: https://school-collection.edu.ru/
4) Federal Center for Information and Educational Resources. – Access mode: https://fcior.edu.ru/
Calendar-thematic planning (mathematics)
| No. | Lesson topic | Number of hours | date | |
| plan | fact | |||
| Chapter 1. Ratios, proportions, percentages | 26 | |||
| 1 – 2 | Relationships between numbers and quantities. | 2 | ||
| 3 – 4 | Scale | 2 | ||
| 5 – 7 | Dividing a number in this ratio. | 3 | ||
| 8 — 10 | Proportions. | 3 | ||
| 11 — 14 | Direct and inverse proportionality. | 4 | ||
| 15 | Test No. 1 on the topic “Relationships. Proportions" | 1 | ||
| 16 -18 | The concept of percentage. | 3 | ||
| 19 — 21 | Problems involving percentages. | 3 | ||
| 22- 23 | Pie charts. | 2 | ||
| 24 — 25 | Historical information. Entertaining tasks. | 2 | ||
| 26 | Test No. 2 on the topic “Interest”. | 1 | ||
| Chapter 2. Integers | 34 | |||
| 27-28 | Negative integers. | 2 | ||
| 29 -30 | Opposite numbers. The absolute value of a number. | 2 | ||
| 31 — 32 | Comparison of integers. | 2 | ||
| 33 — 37 | Addition of integers. | 5 | ||
| 38 — 39 | Laws of addition of integers. | 2 | ||
| 40 — 43 | Difference of integers. | 4 | ||
| 44 -46 | Product of integers. | 3 | ||
| 47 — 49 | Quotient of integers. | 3 | ||
| 50 -51 | Distributive law. | 2 | ||
| 52 — 53 | Expanding parentheses and enclosing parentheses. | 2 | ||
| 54 — 55 | Actions with sums of several terms. | 2 | ||
| 56 — 57 | Representation of integers on a coordinate axis. | 2 | ||
| 58 | Test No. 3 on the topic “Integers” | 1 | ||
| 59 — 60 | Historical information. Entertaining tasks. | 2 | ||
| Chapter 3. Rational numbers | 38 | |||
| 61 — 62 | Negative fractions. | 2 | ||
| 63 — 64 | Rational numbers. | 2 | ||
| 65 — 67 | Comparison of rational numbers. | 3 | ||
| 68 — 72 | Adding fractions and subtracting fractions. | 5 | ||
| 73 — 76 | Multiplying and dividing fractions. | 4 | ||
| 77 — 78 | Laws of addition and multiplication. | 2 | ||
| 79 | Test No. 4 on the topic “Rational numbers” | 1 | ||
| 80 -84 | Mixed fractions of arbitrary sign. | 5 | ||
| 85 — 87 | Representation of rational numbers on the coordinate axis. | 3 | ||
| 88 — 91 | Equations. | 4 | ||
| 92 — 95 | Solving problems using equations. | 4 | ||
| 96 | Test No. 5 on the topic “Equations”. | 1 | ||
| 97 -98 | Historical information. Entertaining tasks. | 2 | ||
| Chapter 4. Decimals. | 34 | |||
| 99 — 100 | The concept of a positive decimal fraction. | 2 | ||
| 101 — 102 | Comparing positive decimals. | 2 | ||
| 103 — 106 | Adding and subtracting positive decimals | 4 | ||
| 107 — 108 | Move the decimal point in a positive decimal. | 2 | ||
| 109 — 112 | Multiplying positive decimals. | 4 | ||
| 113-116 | Dividing positive decimals. | 4 | ||
| 117 | Test No. 6 on the topic “Actions with decimals.” | 1 | ||
| 118 — 121 | Decimals and percentages. | 4 | ||
| 122-123 | Decimal fractions of arbitrary sign. | 2 | ||
| 124 — 126 | Approximation of decimal fractions. | 3 | ||
| 127 -129 | Approximation of the sum, difference, product and quotient of two numbers. | 3 | ||
| 130 | Test No. 7 on the topic “Fractions and percentages.” | 1 | ||
| 131 -132 | Historical information. Entertaining tasks. | 2 | ||
| Chapter 5. Ordinary and decimal fractions | 24 | |||
| 133-134 | Factoring a positive decimal into a final decimal. | 2 | ||
| 136 — 136 | Periodic decimals. | 2 | ||
| 137 -138 | Non-periodic decimal fractions. | 2 | ||
| 139 — 141 | Length of the segment. | 3 | ||
| 142 -144 | Circumference. Area of a circle. | 3 | ||
| 145 — 147 | Coordinate axis. | 3 | ||
| 148 — 150 | Cartesian coordinate system on a plane. | 3 | ||
| 151 — 153 | Column charts and graphs. | 3 | ||
| 154 | Test No. 8 on the topic “Ordinary and decimal fractions.” | 1 | ||
| 155 — 156 | Historical information. Entertaining tasks. | 2 | ||
| Repetition | 14 | |||
| 157 — 158 | Repetition. Actions with fractions. | 2 | ||
| 159 – 160 | Repetition. Operations with decimal fractions. | 2 | ||
| 161 -162 | Repetition. Equations and problems for composing equations. | 2 | ||
| 163 — 164 | Repetition. Percentages and proportions. | 2 | ||
| 165 | Repetition. Constructions in a coordinate system. | 1 | ||
| 166 -167 | Repetition. Adding and subtracting decimals. | 2 | ||
| 168 | Repetition. Multiplying and dividing decimals. | 1 | ||
| 169 | Final test. | 1 | ||
| 170 | Work on mistakes. | 1 | ||
| 171 -172 | Entertaining tasks. | 2 | ||
| 173 — 175 | Time reserve. Repetition. | 3 | ||
The easiest one is Russian
SanPINs, which require sixth-graders to spend 2.5 hours on self-study, highlight mathematics as the most difficult subject - as much as 13 points. Next come Russian and foreign. Among the easiest are fine arts, music and works.
Article on the topic
How much does a fiver cost? Who sells crafts to parents for school and why?
My daughter came home from school at 2 p.m. I had lunch and rested until 16. So, at 4 o’clock I start my lessons. Deep down, I was happy that I would finish them in a couple of hours. Since schoolchildren have to do their homework in 2.5 hours, I’ll try to do it as quickly as possible.
Exercise No. 245 in the Russian language does not cause any difficulties. Rewrite the words, highlight the suffixes, write words with the same root in brackets that allow you to parse the words. I spend 30 minutes on an item.
“Mom, I’m hungry,” the daughter begins to whine, while she was just sitting next to her. - I'm tired. Let’s have some tea, and then I’ll read the story, and in the evening I’ll write English.”
Probably, this - the reluctance of children to concentrate on doing their homework - is the reason that all their free time is spent on them, I think. Yes, it’s difficult, yes, you’re reluctant, but you can sit down and do everything assigned at once, without distractions, and then eat, walk, watch TV, relax.
When drawing up the above recommendations, by the way, it was taken into account that children have different capabilities and unequal labor productivity. Therefore, it is clear that average data are given. But it is recommended to still focus on them.
An hour passes while the child eats and rests. We don’t take it while doing homework.
Work program 6th grade
EXPLANATORY NOTE
The mathematics program for primary school is compiled in accordance with: the requirements of the Federal State Educational Standard for Basic General Education (FSES LLC); requirements for the results of mastering the main educational program (personal, meta-subject, subject); the main approaches to the development and formation of universal learning activities (ULA) for basic general education. It maintains continuity with the federal state educational standard for primary general education; the age and psychological characteristics of schoolchildren studying at the level of basic general education are taken into account, and interdisciplinary connections are taken into account.
The program is based on the author's mathematics program for grades 5–9 of general education institutions. Mathematics: programs for grades 5–9/A.G. Merzlyak, V.B. Polonsky, M.S. Yakir, E.V. Butsko.–M.: Ventana-Graf
The work program in mathematics for grade 6 is compiled on the basis of the Federal component of the state standard of secondary (complete) general education, an approximate program in mathematics for grade 6, edited by A.G. Mordkovich.
Planned results of studying the subject:
Personal results
training are:
1) the ability to clearly, accurately, competently express one’s thoughts in oral and written speech, understand the meaning of the task, build an argument, give examples and counterexamples;
2) critical thinking, the ability to recognize logically incorrect statements, to distinguish a hypothesis from a fact;
3) an idea of mathematical science as a sphere of human activity, of the stages of its development, of its significance for the development of civilization;
4) creativity of thinking, initiative, resourcefulness, activity in solving mathematical problems;
5) the ability to control the process and result of educational mathematical activity;
6) the ability to emotionally perceive mathematical objects, problems, solutions, and reasoning.
Meta-subject results
training are:
1) initial ideas about the ideas and methods of mathematics as a universal language of science and technology, a means of modeling phenomena and processes;
2) the ability to see a mathematical problem in the context of a problem situation in other disciplines, in the surrounding life;
3) the ability to find in various sources the information necessary to solve mathematical problems and present it in an understandable form; make decisions in conditions of incomplete and redundant, accurate and probabilistic information;
4) the ability to understand and use mathematical visual aids (graphs, diagrams, tables, diagrams, etc.) for illustration, interpretation, argumentation;
5) the ability to put forward hypotheses when solving educational problems and understand the need to test them;
6) the ability to use inductive and deductive methods of reasoning, to see different strategies for solving problems;
7) understanding the essence of algorithmic instructions and the ability to act in accordance with the proposed algorithm;
 the ability to independently set goals, select and create algorithms for solving educational mathematical problems;
the ability to independently set goals, select and create algorithms for solving educational mathematical problems;
9) the ability to plan and carry out activities aimed at solving research problems.
General subject results
training are:
1) mastery of the basic conceptual apparatus for the main sections of content; an understanding of the basic concepts being studied (number, geometric figure, equation) as the most important mathematical models that allow one to describe and study real processes and phenomena;
2) the ability to work with mathematical text (analyze, extract the necessary information), accurately and competently express one’s thoughts in oral and written speech using mathematical terminology and symbols, use various languages of mathematics, carry out classifications, logical justifications, proofs of mathematical statements;
3) development of ideas about number and number systems from natural to real numbers; mastering the skills of oral, written, instrumental calculations;
4) mastery of the basic methods of presenting and analyzing statistical data; presence of ideas about statistical patterns in the real world and about various ways of studying them, about probabilistic models;
5) mastery of geometric language, the ability to use it to describe objects in the surrounding world; development of spatial concepts and visual skills, acquisition of skills in geometric constructions;
6) the ability to measure the lengths of segments, the magnitude of angles, and use formulas to find the perimeters, areas and volumes of geometric figures;
7) the ability to apply learned concepts, results, methods to solve problems of a practical nature and problems from related disciplines using, if necessary, reference materials, a calculator, and a computer.
Contents of the subject:
| № p/p | Subject | Quantity hours | Main types of educational activities |
| 1 | Repetition of the 5th grade course | 4 | Theoretical course 5th grade |
| 2 | Positive and negative numbers. Coordinates | 77 | Ideas about rotation, about centrally symmetrical figures, about positive and negative numbers and the coordinate line, about opposite numbers, about integers and rational numbers, about the modulus of a number, about comparing numbers using the coordinate line., about comparing numbers, about parallel lines, about the trapezoid and parallelogram, about moving along a coordinate line, about the operations of addition and subtraction for numbers of different signs, about the rule for calculating an algebraic sum, about opposite numbers, about the distance between points, about the modulus of the difference and the sum of two numbers, about numerical intervals, about non-strict and strict inequalities, about the numerical segment and interval, the rule of multiplication and division of negative numbers, the distributive law of multiplication relative to subtraction, about the coordinates of an object, about the multiplication and division of ordinary fractions, about the multiplication of mixed numbers, about dividing a number by an ordinary fraction, about enumerating all possible options, about combinatorial problems, about the tree of possible options, about the multiplication rule. |
| 3 | Converting literal expressions | 43 | Ideas about the distributive law of multiplication, the rule for opening parentheses, the rule for bringing similar terms, the rules for solving equations, bringing similar terms, opening parentheses, simplifying the expression of the left side of the equation, how to create a mathematical model of a real situation, how to find a part of a whole and a whole according to its part, how to solve problems by parts, about a circle, about the length of a circle, about the formula for the length of a circle, about a regular polygon, how to derive the formula for the area of a circle, using it, find the value of the area for various values of the radius, about the ball, sphere, about the formula area of a sphere, the formula for the volume of a sphere. |
| 4 | Divisibility of natural numbers | 39 | Ideas about GCD and NOC; about the signs of divisibility of a work; properties of divisibility of sum and difference; about the signs of divisibility by 2, 5, 20, 4 and 25; about the signs of divisibility by 3 and 9, about the sum of digit terms; about prime numbers, composite numbers, about twin numbers, about prime factorization, about the fundamental theorem of arithmetic; about GCD and the rule for finding it; about coprime numbers, about the test for divisibility by a product. |
| 5 | Mathematics is all around us. | 38 | Ideas about the relationship of two numbers, about proportions, about the basic property of proportion; about different charts: columnar, pie, graphic and their construction using Excel on a computer; concepts of proportional quantities and scale; about proportion, about correct proportion, about the basic property of proportion, about solving problems on proportions; the principle of solving problems on composing equations, percentages, proportions, and motion; what is a reliable event, an impossible event, a random event, one hundred percent probability, zero probability, equally probable events; how to characterize any event by determining its quantitative characteristics. |
| 6 | Repetition for the 6th grade course. | 9 | Basic rules, concepts for the 6th grade course. |
THEMATIC PLANNING
| № lesson | Lesson topic | Number of hours | date | |||||
| plan | fact | |||||||
| Chapter I. _ Positive and negative numbers (74 + 3 hours) | ||||||||
| 1-4 | Repetition of 5th grade material | 4 | 02.09 05.09 06.09 06.09 | |||||
| 5 | Rotation and central symmetry. | 1 | 07.09 | |||||
| 6 | Rotation and central symmetry. | 1 | 08.09 | |||||
| 7 | Rotation and central symmetry. | 1 | 09.09 | |||||
| 8 | Rotation and central symmetry. | 1 | 12.09 | |||||
| 9 | Rotation and central symmetry. | 1 | 13.09 | |||||
| 10 | Rotation and central symmetry. | 1 | 13.09 | |||||
| 11 | Positive and negative numbers. Coordinate line. | 1 | 14.09 | |||||
| 12 | Positive and negative numbers. Coordinate line. | 1 | 15.09 | |||||
| 13 | Positive and negative numbers. Coordinate line. | 1 | 16.09 | |||||
| 14 | Opposite numbers. The absolute value of a number. | 1 | 19.09 | |||||
| 15 | Opposite numbers. The absolute value of a number. | 1 | 20.09 | |||||
| 16 | Opposite numbers. The absolute value of a number. | 1 | 20.09 | |||||
| 17 | Comparison of numbers. | 1 | 21.09 | |||||
| 18 | Comparison of numbers. | 1 | 22.09 | |||||
| 19 | Comparison of numbers. | 1 | 23.09 | |||||
| 20 | Parallelism of lines. | 1 | 26.09 | |||||
| 21 | Test No. 1. | 1 | 27.09 | |||||
| 22 | Numeric expressions containing +, - signs. | 1 | 27.09 | |||||
| 23 | Numeric expressions containing +, - signs. | 1 | 28.09 | |||||
| 24 | Numeric expressions containing +, - signs. | 1 | 29.09 | |||||
| 25 | Numeric expressions containing +, - signs. | 1 | 30.09 | |||||
| 26 | Numeric expressions containing +, - signs. | 1 | 03.10 | |||||
| 27 | Numeric expressions containing +, - signs. | 1 | 04.10 | |||||
| 28 | Algebraic sum and its properties. | 1 | 04.10 | |||||
| 29 | Algebraic sum and its properties. | 1 | 05.10 | |||||
| 30 | Algebraic sum and its properties. | 1 | 06.10 | |||||
| 31 | Algebraic sum and its properties. | 1 | 07.10 | |||||
| 32 | Algebraic sum and its properties. | 1 | 10.10 | |||||
| 33 | Algebraic sum and its properties. | 1 | 11.10 | |||||
| 34 | The rule for calculating the value of the algebraic sum of two numbers. | 1 | 11.10 | |||||
| 35 | The rule for calculating the value of the algebraic sum of two numbers. | 1 | 12.10 | |||||
| 36 | The rule for calculating the value of the algebraic sum of two numbers. | 1 | 13.10 | |||||
| 37 | The rule for calculating the value of the algebraic sum of two numbers. | 1 | 14.10 | |||||
| 38 | The distance between points on a coordinate line. | 1 | 17.10 | |||||
| 39 | The distance between points on a coordinate line. | 1 | 18.10 | |||||
| 40 | The distance between points on a coordinate line. | 1 | 18.10 | |||||
| 41 | The distance between points on a coordinate line. | 1 | 19.10 | |||||
| 42 | Axial symmetry. | 1 | 20.10 | |||||
| 43 | Axial symmetry. | 1 | 21.10 | |||||
| 44 | Axial symmetry. | 1 | 24.10 | |||||
| 45 | Reserve. | 1 | 25.10 | |||||
| 46 | Numerical intervals. | 1 | 25.10 | |||||
| 47 | Numerical intervals. | 1 | 26.10 | |||||
| 48 | Numeric intervals | 1 | 27.10 | |||||
| 49 | Numeric intervals | 1 | 28.10 | |||||
| 50 | Test No. 2. | 1 | 07.11 | |||||
| 51-53 | Reserve | 3 | 08.11 08.11 09.11 | |||||
| 54 | Multiplying and dividing positive and negative numbers. | 1 | 10.11 | |||||
| 55 | Multiplying and dividing positive and negative numbers. | 1 | 11.11 | |||||
| 56 | Multiplying and dividing positive and negative numbers. | 1 | 14.11 | |||||
| 57 | Multiplying and dividing positive and negative numbers. | 1 | 15.11 | |||||
| 58 | Multiplying and dividing positive and negative numbers. | 1 | 15.11 | |||||
| 59 | Multiplying and dividing positive and negative numbers. | 1 | 16.11 | |||||
| 60 | Multiplying and dividing positive and negative numbers. | 1 | 17.11 | |||||
| 61 | Coordinates. | 1 | 18.11 | |||||
| 62 | Coordinates. | 1 | 21.11 | |||||
| 63 | Coordinate plane. | 1 | 22.11 | |||||
| 64 | Coordinate plane. | 1 | 22.11 | |||||
| 65 | Coordinate plane. | 1 | 23.11 | |||||
| 66 | Coordinate plane. | 1 | 24.11 | |||||
| 67 | Coordinate plane. | 1 | 25.11 | |||||
| 68 | Multiplying and dividing ordinary fractions. | 1 | 28.11 | |||||
| 69 | Multiplying and dividing ordinary fractions. | 1 | 29.11 | |||||
| 70 | Multiplying and dividing ordinary fractions. | 1 | 29.11 | |||||
| 71 | Multiplying and dividing ordinary fractions. | 1 | 30.11 | |||||
| 72 | Multiplying and dividing ordinary fractions. | 1 | 01.12 | |||||
| 73 | Multiplying and dividing ordinary fractions. | 1 | 02.12 | |||||
| 74 | Multiplying and dividing ordinary fractions. | 1 | 05.12 | |||||
| 75 | Multiplying and dividing ordinary fractions. | 1 | 06.12 | |||||
| 76 | Multiplication rule for combinatorial problems. | 1 | 06.12 | |||||
| 77 | Multiplication rule for combinatorial problems. | 1 | 07.12 | |||||
| 78 | Multiplication rule for combinatorial problems. | 1 | 08.12 | |||||
| 79 | Reserve | 1 | 09.12 | |||||
| 80 | Test No. 3. | 1 | 12.12 | |||||
| Chapter II . Converting literal expressions (41 + 2 hours) | ||||||||
| 81 | Expanding parentheses. | 1 | 13.12 | |||||
| 82 | Expanding parentheses. | 1 | 13.12 | |||||
| 83 | Expanding parentheses. | 1 | 14.12 | |||||
| 84 | Expanding parentheses. | 1 | 15.12 | |||||
| 85 | Expanding parentheses. | 1 | 16.12 | |||||
| 86 | Simplifying expressions. | 1 | 19.12 | |||||
| 87 | Simplifying expressions. | 1 | 20.12 | |||||
| 88 | Simplifying expressions. | 1 | 20.12 | |||||
| 89 | Simplifying expressions. | 1 | 21.12 | |||||
| 90 | Simplifying expressions. | 1 | 22.12 | |||||
| 91 | Simplifying expressions. | 1 | 23.12 | |||||
| 92 | Solving equations. | 1 | 26.12 | |||||
| 93 | Solving equations. | 1 | 27.12 | |||||
| 94 | Solving equations. | 1 | 27.12 | |||||
| 95 | Solving equations | 1 | 28.12 | |||||
| 96 | Solving equations | 1 | 29.12 | |||||
| 97 | Solving equations | 1 | 30.12 | |||||
| 98 | Solving equation problems | 1 | 09.01 | |||||
| 99 | Solving equation problems | 1 | 10.01 | |||||
| 100-101 | Reserve | 2 | 10.01 11.01 | |||||
| 102 | Solving equations. Solving equation problems | 1 | 12.01 | |||||
| 103 | Solving equations. Solving equation problems | 1 | 13.01 | |||||
| 104 | Solving equations. Solving equation problems | 1 | 16.01 | |||||
| 105 | Solving equations. Solving equation problems | 1 | 17.01 | |||||
| 106 | Solving equations. Solving equation problems | 1 | 17.01 | |||||
| 107 | Test No. 4. | 1 | 18.01 | |||||
| 108 | Two basic fraction problems | 1 | 19.01 | |||||
| 109 | Two basic fraction problems | 1 | 20.01 | |||||
| 110 | Two basic fraction problems | 1 | 23.01 | |||||
| 111 | Two basic fraction problems | 1 | 24.01 | |||||
| 112 | Circle. Circumference | 1 | 24.01 | |||||
| 113 | Circle. Circumference | 1 | 25.01 | |||||
| 114 | Circle. Circumference | 1 | 26.01 | |||||
| 115 | Circle. Circumference | 1 | 27.01 | |||||
| 116 | Circle. Area of a circle | 1 | 30.01 | |||||
| 117 | Circle. Area of a circle | 1 | 31.01 | |||||
| 118 | Circle. Area of a circle | 1 | 31.01 | |||||
| 119 | Circle. Area of a circle | 1 | 01.02 | |||||
| 120 | Ball. Sphere | 1 | 02.02 | |||||
| 121 | Ball. Sphere | 1 | 03.02 | |||||
| 122-123 | Reserve | 1 | 06.02 | |||||
| 124 | Test No. 5. | 1 | 07.02 | |||||
| Chapter III . Divisibility of natural numbers.(37 + 2 hours) | ||||||||
| 125 | Divisors and multiples | 1 | 07.02 | |||||
| 126 | Divisors and multiples | 1 | 08.02 | |||||
| 127 | Divisors and multiples | 1 | 09.02 | |||||
| 128 | Divisibility of a product | 1 | 10.02 | |||||
| 129 | Divisibility of a product | 1 | 13.02 | |||||
| 130 | Divisibility of a product | 1 | 14.02 | |||||
| 131 | Divisibility of a product | 1 | 14.02 | |||||
| 132 | Divisibility of sum and difference of numbers | 1 | 15.02 | |||||
| 133 | Divisibility of sum and difference of numbers | 1 | 16.02 | |||||
| 134 | Divisibility of sum and difference of numbers | 1 | 17.02 | |||||
| 135 | Divisibility of sum and difference of numbers | 1 | 20.02 | |||||
| 136 | Divisibility of sum and difference of numbers | 1 | 21.02 | |||||
| 137 | Tests for divisibility by 2, 5, 10, 4 and 25 | 1 | 21.02 | |||||
| 138 | Tests for divisibility by 2, 5, 10, 4 and 25 | 1 | 22.02 | |||||
| 139 | Tests for divisibility by 2, 5, 10, 4 and 25 | 1 | 23.02 | |||||
| 140 | Tests for divisibility by 2, 5, 10, 4 and 25 | 1 | 24.02 | |||||
| 141 | Tests for divisibility by 3 and 9 | 1 | 27.02 | |||||
| 142 | Tests for divisibility by 3 and 9 | 1 | 28.02 | |||||
| 143 | Tests for divisibility by 3 and 9 | 1 | 28.02 | |||||
| 144 | Tests for divisibility by 3 and 9 | 1 | 01.03 | |||||
| 145 | Test No. 6. | 1 | 02.03 | |||||
| 146 | Prime numbers. Factoring a number into prime factors | 1 | 03.03 | |||||
| 147 | Prime numbers. Factoring a number into prime factors | 1 | 06.03 | |||||
| 148 | Prime numbers. Factoring a number into prime factors | 1 | 07.03 | |||||
| 149 | Prime numbers. Factoring a number into prime factors | 1 | 07.03 | |||||
| 150 | Prime numbers. Factoring a number into prime factors | 1 | 08.03 | |||||
| 151 | Greatest common divisor | 1 | 09.03 | |||||
| 152 | Greatest common divisor | 1 | 10.03 | |||||
| 153 | Greatest common divisor | 1 | 13.03 | |||||
| 154 | Greatest common divisor | 1 | 14.03 | |||||
| 155 | Mutually prime numbers. Divisibility test for a product. Least common multiple | 1 | 14.03 | |||||
| 156 | Mutually prime numbers. Divisibility test for a product. Least common multiple | 1 | 15.03 | |||||
| 157 | Mutually prime numbers. Divisibility test for a product. Least common multiple | 1 | 16.03 | |||||
| 158 | Mutually prime numbers. Divisibility test for a product. Least common multiple | 1 | 17.03 | |||||
| 159 | Test No. 7 | 1 | 20.03 | |||||
| 160-163 | Reserve | 4 | 21.03 21.03 22.03 23.03 | |||||
| Chapter IV . Mathematics around us.(46 +1 hour) | ||||||||
| 164 | Ratio of two numbers | 1 | 24.03 | |||||
| 165 | Ratio of two numbers | 1 | 03.04 | |||||
| 166 | Ratio of two numbers | 1 | 04.04 | |||||
| 167 | Ratio of two numbers | 1 | 04.04 | |||||
| 168 | Ratio of two numbers | 1 | 05.04 | |||||
| 169 | Diagrams | 1 | 06.04 | |||||
| 170 | Diagrams | 1 | 07.04 | |||||
| 171 | Diagrams | 1 | 10.04 | |||||
| 172 | Diagrams | 1 | 11.04 | |||||
| 173 | Proportionality of quantities | 1 | 11.04 | |||||
| 174 | Proportionality of quantities | 1 | 12.04 | |||||
| 175 | Proportionality of quantities | 1 | 13.04 | |||||
| 176 | Proportionality of quantities | 1 | 14.04 | |||||
| 177 | Proportionality of quantities | 1 | 17.04 | |||||
| 178 | Solving problems using proportions | 1 | 18.04 | |||||
| 179 | Solving problems using proportions | 1 | 18.04 | |||||
| 180 | Solving problems using proportions | 1 | 19.04 | |||||
| 181 | Solving problems using proportions | 1 | 20.04 | |||||
| 182 | Solving problems using proportions | 1 | 21.04 | |||||
| 183 | Solving problems using proportions | 1 | 24.04 | |||||
| 184 | Test No. 8 on the topic “Proportion” | 1 | 25.04 | |||||
| 185 | Miscellaneous tasks | 1 | 25.04 | |||||
| 186 | Miscellaneous tasks | 1 | 26.04 | |||||
| 187 | Miscellaneous tasks | 1 | 27.04 | |||||
| 188 | Miscellaneous tasks | 1 | 28.04 | |||||
| 189 | Miscellaneous tasks | 1 | 04.05 | |||||
| 190 | Miscellaneous tasks | 1 | 05.05 | |||||
| 191 | Miscellaneous tasks | 1 | 08.05 | |||||
| 192 | Miscellaneous tasks | 1 | 10.05 | |||||
| 193 | First introduction to the concept of probability | 1 | 11.05 | |||||
| 194 | First introduction to the concept of probability | 1 | 12.05 | |||||
| 195 | First introduction to the concept of probability | 1 | 15.05 | |||||
| 196 | First introduction to probability calculation | 1 | 16.05 | |||||
| 197 | First introduction to probability calculation | 1 | 16.05 | |||||
| 198 | First introduction to probability calculation | 1 | 17.05 | |||||
| 199-201 | Reserve | 3 | 18.05 19.05 22.05 | |||||
| 202 | Repetition. Algebraic sum and its properties | 1 | 23.05 | |||||
| 203 | Repetition. Multiplying and dividing common fractions | 1 | 23.05 | |||||
| 204 | Repetition. Expanding parentheses. Simplifying Expressions | 1 | 24.05 | |||||
| 205 | Repetition. Solving equations. Solving equation problems | 1 | 25.05 | |||||
| 206 | Repetition. Finding a part from a whole and a whole from its part | 1 | 26.05 | |||||
| 207 | Repetition. Signs of divisibility. | 1 | 29.05 | |||||
| 208 | Repetition. Greatest common divisor and least common multiple. | 1 | 30.05 | |||||
| 209-210 | Final test | 2 | 30.05 31.05 | |||||
Work program adjustment sheet
| No. | Title of section, topic | Scheduled date | Reason for adjustment | Corrective measures, details of the document that confirms the change | Actual date |
15
"Unsolvable" mathematics
The child does not have a math assignment in his diary. “They gave the Olympics to the house,” explains the daughter. — There are 6 tasks, each is worth 10-20 points. In general, the teacher told us to decide as we want, because this is a qualifying stage. The winners will go to the university to take final tests.”
I was surprised: why is such a task given at home? It is clear that children will resort to the help of their parents. I received the answer to my question when I started solving problems.
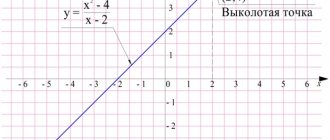
At first there were tasks that were more or less understandable. Of course, it’s difficult to call them easy, but after thinking and searching the Internet for similar ones, I managed. But the third one threw me into a stupor: “There are 10 liters of water in a certain vessel, and the second one is empty. From the first vessel half of the water in it is poured into the second, then from the second 1/3 of the water into the first, then from the first 1/4 into the second, then from the second 1/5 into the first. What amount of water will be in the first transfusion after 2017?” A group of parents in our class on Viber send each other possible solutions. With two unknowns, an equation, on a coordinate axis, using graphs... All answers vary. Or rather, they simply don’t exist. Having killed an hour and still not finding a solution, I go online for help. Unfortunately, there is no such task on the Internet either. Then I use the “heavy artillery.” Friends, graduates of the Chelyabinsk Physics and Mathematics Lyceum, have already helped me solve similar complex tasks several times. I’m making a post on social media asking for help with a problem. The answer is written by one of the graduates: for some reason, after each odd transfusion, both vessels will contain the same amount of water. The girl says that this is easy to prove by induction. What is induction like in sixth grade? I am writing the answer - 5 liters - not sure that it will be accepted without a decision. But God be with him. The Olympics and Russian took me two hours of pure time. According to SanPIN, the remaining time is history and English for half an hour. We need to speed up!
It was getting dark, but I continued to study the history of the Middle Ages. Photo: AiF/ Nadezhda Uvarova
Mathematics work program
- Explanatory note
The work program of the mathematics curriculum for grade 6 is compiled on the basis of an approximate program of basic general education in mathematics (collection of programs of general education institutions in mathematics for grades 5–6. M. Prosveshcheniye, 2009, compiled by T.A. Burmistrova) in accordance with the federal component of the state educational standard basic general education, taking into account the specifics of learning material by students in a special (correctional) class of type VII (for children with mental retardation).
This work program was compiled for studying mathematics using the textbook: Mathematics. textbook for 6th grade of educational institutions / N.Ya Vilenkin. and others. M.: Mnemosyne 2012.
Work program level
base
Regulatory legal documents on the basis of which the work program was developed:
- Federal Law of December 29, 2012 No. 273-FZ (as amended on May 7, 2013) “On Education in the Russian Federation”
- The federal component of the state educational standard of general education, approved by Order of the Ministry of Education of the Russian Federation dated 03.05.2004 No. 1089 “On approval of the federal component of state standards of primary general, basic general and secondary (complete) general education” (as amended by the orders of the Ministry of Education and Science of the Russian Federation dated 03.06 .2008 No. 164, dated August 31, 2009, No. 320, dated October 19, 2009, No. 427);
- Order of the Ministry of Education and Science of the Russian Federation dated December 19, 2012 No. 1067 “On approval of federal lists of textbooks recommended (approved) for use in the educational process in educational institutions implementing educational programs of general education and having state accreditation for the 2013/2014 academic year »
This mathematics program is a logical continuation of the continuous mathematics course in general education schools. While maintaining the basic content of education adopted for mass schools, it differs in that it provides for a corrective focus of education.
Taking into account the characteristics of students in class VII type, the program uses verbal, practical and visual methods that:
· have a clear structure and graphical highlighting of conclusions, the most important provisions, and key concepts;
· contain a sufficient number of illustrations to facilitate perception and understanding of the material;
· stimulate students to develop independence in solving assigned educational tasks;
· develop the ability to use existing knowledge.
In the program for children with mental retardation, the practical orientation of training is strengthened.
One of the techniques used in the lesson is algorithmization. These are various instruction manuals that record the sequence of actions when solving equations, problems, and difficult cases of multiplication and division. To solve arithmetic problems, visual operations or a drawing are used.
Taking into account the characteristics of children with disabilities, this program eliminates cumbersome computational operations and selects numbers that are composite and with the help of which various calculations are easily carried out. The problems are offered with the most accessible content and the simplest formulation; equations are solved only by finding one component, with a simple opening of parentheses and bringing similar terms.
The volume of material studied allows for a slow pace of progress through the course. In the 6th grade, enough time is allocated for practicing basic skills that meet the mandatory requirements, for repetition, including correction of knowledge and skills for the 5th grade and elementary school.
2.
General characteristics of the academic subject
Mathematics education in the 6th grade consists of the following content components (exact names of blocks): arithmetic; algebra; geometry; elements of combinatorics, probability theory, statistics.
Arithmetic
designed to facilitate the acquisition of practical skills necessary for everyday life. It serves as the basis for all further study of mathematics, promotes logical development and the formation of the ability to use algorithms.
Algebra
is aimed at developing a mathematical apparatus for solving problems in mathematics, related subjects, and the surrounding reality.
Geometry
– one of the most important components of mathematical education, necessary for the acquisition of specific knowledge about space and practically significant skills, the formation of a language for describing objects in the surrounding world, for the development of spatial imagination and intuition, mathematical culture, and for the aesthetic education of students. The study of geometry contributes to the development of logical thinking and to the formation of the concept of proof.
Elements of logic, combinatorics, statistics and probability theory
necessary, first of all, for the formation of functional literacy - the ability to perceive and analyze information presented in various forms, understand the probabilistic nature of many real dependencies, and make simple probabilistic calculations.
Learning the basics of combinatorics
will allow the student to consider cases, enumerate and count the number of options, including in the simplest applied problems. When studying statistics and probability theory, ideas about the modern picture of the world and methods of its research are enriched, an understanding of the role of statistics as a source of socially significant information is formed, and the foundations of probabilistic thinking are laid.
Knowledge of mathematics is important in everyday life: purchasing food, clothing, household items, paying for apartments and other utilities, calculating the amount of materials for repairs, related contributions, etc. In addition, children need mathematical knowledge when mastering other educational subjects such as technology, chemistry, geography, physics.
The purpose of studying mathematics in the 6th grade is to systematically develop the concept of number, develop the ability to perform oral and written arithmetic operations on positive and negative numbers and ordinary fractions, translate practical problems into the language of mathematics, and prepare students to study systematic courses in algebra and geometry. Serious attention is paid to developing the ability to reason, make simple proofs, and provide justification for actions taken. In the future, the knowledge and skills acquired while studying mathematics will become necessary for mastering available professional and labor skills.
3.
Place of the subject “Mathematics” in the curriculum
According to the federal basic curriculum, 170 hours per academic year are allocated for the study of mathematics in 6 grades at the rate of 5 hours per week.
4.
Contents of the program
1.
Repetition - 3 hours.
Ordinary fractions with the same denominator. Decimal fractions and operations with them. Interest. Angles. Coordinate beam.
The main goal is to repeat the theoretical material of the 5th grade mathematics course.
2. Divisibility of numbers (14 hours).
Divisors and multiples. Common divisor and common multiple. Signs of divisibility by 2, 3, 5, 10. Prime and composite numbers. Factoring a natural number into prime factors.
The main goal is to complete the study of natural numbers, to prepare the basis for mastering operations with ordinary fractions.
This topic concludes the study of issues related to natural numbers. The main focus should be on becoming familiar with the concepts of divisor and multiple, which are used in reducing fractions and reducing them to a common denominator. It is useful to perform exercises based on the multiplication table by direct selection. The concepts of “greatest common divisor” and “least common multiple”, along with algorithms for finding them, need not be considered.
Some attention is paid to familiarization with the signs of divisibility, the concepts of prime and composite numbers. When studying them, it is advisable to develop the ability to draw simple conclusions, justifying your actions with references to a definition or rule.
Students should be able to factor a number. For example, they should understand that 36 = 6 • 6 = 4 • 9. The question of factoring a number into prime factors is optional.
3. Addition and subtraction of fractions with different denominators (23 hours).
The main property of a fraction. Reducing fractions. Reducing fractions to a common denominator. The concept of the lowest common denominator of several fractions. Comparing fractions. Adding and subtracting fractions. Solving word problems.
The main goal is to develop strong skills in converting fractions, adding and subtracting fractions.
One of the most important learning outcomes is the mastery of the basic properties of fractions used to convert fractions: reduction, reduction to a new denominator. In this case, it is recommended to present the material without relying on the concepts of GCD and NOC. The ability to reduce fractions to a common denominator is used to compare fractions.
When considering operations with fractions, the rules for adding and subtracting fractions with the same denominators and the concept of a mixed number are used. It is important to pay attention to the case of subtracting a fraction from a whole number. As for the addition and subtraction of mixed numbers, which do not find active use in subsequent study of the course, students should only get an idea of the fundamental possibility of performing such actions.
4.
Multiplication and division of ordinary fractions (29 hours).
Multiplying and dividing ordinary fractions. Basic fraction problems.
The main goal is to develop strong skills in fraction arithmetic and solving basic fraction problems.
This topic completes the development of skills in arithmetic operations with ordinary fractions. The skills must be strong enough so that students do not experience difficulties in calculations with rational numbers, so that algorithms for operations with ordinary fractions can later become the basis for developing the ability to perform operations with algebraic fractions.
Expansion of the apparatus of operations with fractions allows you to solve text problems in which you need to find a fraction from a number or a number from a given value of its fraction, performing multiplication or division by a fraction, respectively.
5.
Relations and proportions (17 hours).
Attitude. Proportion. The main property of proportion. Solving problems using proportions. Concepts of direct and inverse proportionality of quantities. Problems on proportions. Scale. The concept of circumference and area of a circle. Ball.
The main goal is to form the concepts of ratio, proportion, direct and inverse proportionality of quantities.
It is necessary that students learn the basic property of proportion, as it is used in mathematics, chemistry, and physics lessons. In particular, sufficient attention should be given to solving percentage problems using proportions.
The concepts of direct and inverse proportionality of quantities can be formed as a generalization of several specific examples, while emphasizing the practical significance of these concepts and the possibility of their use to simplify the solution of relevant problems.
This topic provides ideas about the circumference and area of a circle. The examination of geometric shapes ends with an introduction to the ball.
6.
Positive and negative numbers (13 hours).
Positive and negative numbers. Opposite numbers. The modulus of a number and its geometric meaning.
Comparison of numbers. Whole numbers. Image of numbers on a line. Point coordinate.
The main goal is to expand students' understanding of number by introducing negative numbers.
The expediency of introducing negative numbers is demonstrated by meaningful examples. Students should learn to draw positive and negative numbers on a coordinate line so that it can serve as a visual basis for the rules for comparing numbers and adding and subtracting numbers discussed in the next topic.
Special attention should be paid to mastering the concept of modulus of a number introduced here, a solid knowledge of which is necessary for developing the ability to compare negative numbers, and subsequently for mastering algorithms for arithmetic operations with positive and negative numbers.
7.
Addition and subtraction of positive and negative numbers (11 hours).
Adding and subtracting positive and negative numbers.
The main goal is to develop strong skills in adding and subtracting positive and negative numbers.
Actions with negative numbers are introduced on the basis of ideas about changes in quantities: addition and subtraction of numbers is illustrated by the corresponding movements of points on the number axis. When studying this topic, addition and subtraction algorithms are purposefully developed when performing operations with integer and fractional numbers.
8.
Multiplication and division of positive and negative numbers (12 hours).
Multiplying and dividing positive and negative numbers. The concept of a rational number. Decimal approximation of a common fraction. Application of the laws of arithmetic operations to rationalize calculations.
The main goal is to develop strong arithmetic skills with positive and negative numbers.
Multiplication and division skills for positive and negative numbers are practiced first by performing individual operations and then in combination with addition and subtraction skills to calculate the meaning of numerical expressions.
As students study this topic, they should learn that to convert a fraction to a decimal, simply divide the numerator by the denominator. In each specific case, they must know which decimal fraction this ordinary fraction turns into - finite or infinite. In this case, it is not necessary to focus on the fact that an infinite decimal fraction turns out to be periodic. Students should know the decimal representation of fractions such as ½, ¼.
9.
Solving equations (15 hours).
The simplest transformations of expressions: opening brackets, bringing similar terms. Solving linear equations. Examples of solving word problems using linear equations.
The main goal is to prepare students to perform transformations of expressions and solve equations.
Transformations of literal expressions by opening parentheses and bringing similar terms are practiced to the extent that they are necessary for solving simple equations.
The introduction of arithmetic operations on negative numbers allows students to become familiar with general techniques for solving linear equations with one unknown.
10.
Coordinates on the plane (10 hours).
Constructing a perpendicular to a straight line and parallel lines using a square and a ruler. Rectangular coordinate system on a plane, abscissa and ordinate of a point. Examples of graphs, diagrams.
The main goal is to introduce students to the rectangular coordinate system on a plane.
Students must learn to recognize and draw perpendicular and parallel lines. The main attention should be paid to developing the skills of constructing them using a ruler and square, without requiring the reproduction of exact definitions.
The main result of students’ familiarization with the coordinate plane should be knowledge of the order of recording the coordinates of points on the plane and their names, the ability to construct coordinate axes, mark a point according to its given coordinates, and determine the coordinates of a point marked on the coordinate plane.
The formation of computational and graphical skills is facilitated by the construction of bar graphs. When performing appropriate exercises, previously learned information about scale and rounding of numbers will be used.
11.
Elements of statistics, combinatorics and probability theory (6 hours)
The concept of random experience and events. Reliable and impossible events. Comparison of odds.
Examples of solving combinatorial problems: enumeration of options, multiplication rule.
While studying the topic, students should
Know:
– concept of probability, multiplication rule.
Be able to:
- collect information in simple cases, present information in the form of tables and diagrams, including using computer tasks;
-give examples of random events, reliable and impossible events. Compare the chances of events occurring;
-to build speech structures using phrases is more likely, unlikely
and etc.
-perform a search of all possible options for recalculating objects or combinations, highlighting combinations that meet the specified conditions.
12. Repetition. Problem solving (17 hours).
5.
Thematic planning
| No. | Topic name | Col. hours |
| 1 | Repetition of the 5th grade mathematics course | 3 |
| 2 | Divisibility of numbers | 14 |
| 3 | Adding and subtracting fractions with different denominators | 23 |
| 4 | Multiplying and dividing common fractions | 29 |
| 5 | Proportions | 17 |
| 6 | Positive and negative numbers | 13 |
| 7 | Adding and subtracting positive and negative numbers | 11 |
| 8 | Multiplying and dividing positive and negative numbers | 12 |
| 9 | Solving equations | 15 |
| 10 | Plane coordinates | 10 |
| 11 | Elements of statistics, combinatorics and probability theory. | 6 |
| 12 | Repetition | 17 |
| Total hours | 170 |
60-70 additional questions
Without being at all upset, I resolutely open the story. The daughter says that even though she has one paragraph written down, the teacher advises reading two: according to the current lesson, in every lesson, without exception, they write a short independent work, and the next one is for easier learning of the new topic.
I read both paragraphs aloud. By the way, they are quite interesting: about Catholicism and the Crusades. Children go through the foreign history of the Middle Ages. I don't remember much from the school curriculum on it, but the information I receive is interesting.
“There are still questions to be answered,” my sixth-grader prompts.
Of course, of course. As I was taught many years ago, after reading a paragraph, I answer the questions at the end of it and retell the text, almost without looking at the textbook. Of course, I’m already tired of lessons, but time is running out. The remaining half hour is spent on the story. English doesn't work.
Article on the topic
Mom, get to your desk! How to teach parents to help their child with homework
“Mom, not these questions,” the daughter giggles. — The teacher gives us independently developed 60-70 additional questions for each paragraph. Well, there aren't necessarily questions there. These can be dates, concepts, and sayings. You need to understand all of them, to know what they are talking about. Independent is just like them. He believes that the textbook provides the bare minimum. And we, in order to be intellectually developed people, must know much more.”
The child opens the supporting materials given by the teacher. My eye starts to twitch: there are 53 and 70 questions for two paragraphs, respectively. Those related to Catholicism contain a number of concepts that are not in the textbook. Frankly, I don’t know what “legate” and “monsegur” are. Who owns and what does the phrase “Beat everyone, the Lord will recognize his own” mean? And most importantly, I doubted whether children at the age of 12 really needed to know all this.
By Googling, I get answers to all my questions. I’ll be honest: this is all very difficult. Especially if you are in sixth grade. Taking into account that there is still a lot of unlearned ahead, and strength is running out. I’m beginning to understand why my daughter’s class currently has an average history score of 2.6, according to the Online Diary.
Having spent another half hour searching for answers and consolidating knowledge, I understand, at a minimum, that I no longer fit into the norms. But English language and literature remained. For the latter, they were asked to read poems expressively. “The teacher said, we will still learn by heart one of Tyutchev’s ,” says the daughter. - So you can learn it today. Well, or until Friday.”
No, I just read the lines and understand: I need a break. I don’t fit into the allotted norm, my head is ringing, my eyes are sticking together and I want to eat.
We are not teaching poetry today, we have no time for it. Photo: AiF/ Nadezhda Uvarova
“GDZ is our everything”
During the break, I consult with the mothers of other children - how are their children doing their homework or are they doing their homework themselves? After all, this, honestly, is incomprehensible to the mind. What if the child studied in depth by attending additional electives?
“I’ve made my life easier a long time ago,” writes the mother of excellent student Olya . - GDZ (ready-made homework - author's note) is our everything. Why does a child need to know so much? We taught ourselves our homework and went to bed at one or two in the morning. And now we find and rewrite. But if the task is given on cards, then yes, you have to do it.”
The general opinion of the majority of mothers in our class, and even parents communicating on social networks, is this: it is unthinkable, and it is not necessary, to shoulder this overwhelming baggage called “homework” in full. Everyone makes life as easy as they can. The most categorical ones say honestly: either lessons or life: “because of homework, neither parents nor children see the white light.”
Closer to ten in the evening I open my English textbook. It is necessary to complete all the exercises from page 36 in the workbook. I am glad that I studied English in educational institutions, and not German or French, I understand... that I do not know the exact answers. I don't remember the grammar. I understand English phrases and can express myself, but it’s still difficult to choose the correct form of an unfamiliar verb. No, this can be done with a dictionary, but then my lessons will end closer to the morning. I, to my shame, copy English from one of the sites with ready-made homework assignments, of which there are dozens on the Internet.
I was exhausted and copied my English from the Internet. Photo: AiF/ Nadezhda Uvarova