Linear equation with two variables
Lesson questions:
· repeat what a linear equation with one variable is and how many solutions such an equation can have;
· introduce the concepts of “linear equation with two variables”, “solving an equation with two variables”, “equivalent equations”.
Lesson material
Previously, we looked at a linear equation with one variable.
Let's remember that:
Today in the lesson we will get acquainted with a linear equation, but with two unknowns.
Let's look at the situation
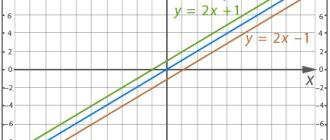
The resulting equality contains two variables. And therefore such equalities are called equations with two variables
(or with two unknowns).
Look at examples of equations in two variables
Let's formulate a definition:
Definition.
Linear equation with two variables
called an equation of the form:
Let's return to the task
That is, a pair of variable values ( x
= 60
,
y = 110
) is a solution to this equation. Note that these roots were found by selection, and this is not the only pair of numbers that satisfy our equation.
Definition.
Solving an equation with two variables
is a pair of variable values that turns this equation into a true equality.
Let us remember that when studying equations with one variable, we talked about equivalent equations, that is, equations that have the same roots.
Similarly, we can say that equations with two variables that have the same solutions are called equivalent
.
Moreover, equations with two variables that have no solutions are also equivalent
.
Equivalent equations have the following properties:
Property 1.
If you move a term in an equation from one part to another, changing its sign, you will get an equation equivalent to the given one;
Property 2.
If both sides of an equation are multiplied (or divided) by the same non-zero number, you get an equation equivalent to the given one.
Let's return to our equation again
But here it is important to know which variable comes first and which comes second. So in our case, the value of the variable x
, and then the variable
y
.
In this case, a couple of numbers (150; — 25)
being a solution to the equation, it does not satisfy the conditions of the problem, since the speed of the car cannot be negative.
And let's look at one more problem.
Example.
The solution of equations in integers, that is, when it is necessary to find only integer values of variables, was considered in detail by the ancient Greek mathematician Diophantus.
Therefore, equations with several variables that must be solved in integers are called Diophantine equations
. That is, the equation compiled in the previous problem is Diophantine, since for it we looked for only natural solutions.
And let's look at examples.
Example.
And another example.
Example.
Lesson summary
So, in this lesson we looked at a linear equation in two variables and one of the ways to solve such equations.
Algebra. Lesson 4. Equations, systems of equations
Watch free video lessons on the Hedgehog Clear channel on the topic “Equations”.
Video lessons on the Hedgehog channel Clearly. Subscribe!
Page content:
- Linear equations
Examples Special cases
- Quadratic equations
Examples
- Factoring a quadratic trinomial
Examples
- Fractional rational equations
Examples
- Systems of equations
Substitution method Addition method
- Examples of solutions to tasks from the OGE
A linear equation is an equation of the form ax = b, where x is a variable, a and b are some numbers, and a ≠ 0.
Examples of linear equations:
- 3 x = 2
- 2 7 x = − 5
Linear equations are called not only equations of the form ax = b, but also any equations that, with the help of transformations and simplifications, are reduced to this form.
How to solve equations that are reduced to the form ax = b? It is enough to divide the left and right sides of the equation by the value a. As a result, we get the answer: x = ba.
How to recognize whether an arbitrary equation is linear or not? You need to pay attention to the variable that is present in it. If the leading power of a variable is equal to one, then such an equation is a linear equation.
In order to solve a linear equation , you need to open the brackets (if any), move the “X’s” to the left side, the numbers to the right, and bring similar terms. The result is an equation of the form ax = b. The solution to this linear equation is: x = ba.
Examples of solving linear equations:
- 2 x + 1 = 2 ( x − 3 ) + 8
This is a linear equation because the variable is to the first power.
Let's try to convert it to the form ax = b :
First, let's open the brackets:
2 x + 1 = 4 x − 6 + 8
All terms with x are transferred to the left side, and numbers to the right:
2 x − 4 x = 2 − 1
− 2 x = 1
Now let's divide the left and right sides by the number (-2):
− 2 x − 2 = 1 − 2 = − 1 2 = − 0.5
Answer: x = − 0.5
- x 2 − 1 = 0
This equation is not a linear equation because the highest power of the variable x is two.
- x ( x + 3 ) − 8 = x − 1
This equation looks linear at first glance, but after opening the parentheses, the leading power becomes equal to two:
x 2 + 3 x − 8 = x − 1
This equation is not a linear equation.
Special cases (they were not encountered in task 4 of the OGE, but it is useful to know them)
Examples:
- 2 x − 4 = 2 ( x − 2 )
This is a linear equation.
Let's open the brackets, move the X's to the left, the numbers to the right: 2 x − 4 = 2 x − 4
2 x − 2 x = − 4 + 4
0 = 0
And how can we look for x here if it doesn’t exist? After performing the transformations, we received the correct equality (identity), which does not depend on the value of the variable x. Whatever value of x we substitute into the original equation, the result always results in a correct equality (identity). This means x can be any number. Let's write down the answer to this linear equation.
Answer: x ∈ ( − ∞ ; + ∞ )
- 2 x − 4 = 2 ( x − 8 )
This is a linear equation. Let's open the brackets, move the X's to the left, numbers to the right:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
0 = − 12
As a result of the transformations, x was reduced, but the result was an incorrect equality, since . No matter what value of x we substitute into the original equation, the result will always be an incorrect equality. This means that there are no values of x at which the equality would become true. Let's write down the answer to this linear equation.
Answer: x ∈ ∅
A quadratic equation is an equation of the form ax 2 + bx + c = 0, where x is a variable, a, b and c are some numbers, and a ≠ 0.
Algorithm for solving a quadratic equation:
- Open the brackets, move all the terms to the left side so that the equation takes the form: ax 2 + bx + c = 0
- Write down what the coefficients are equal to in numbers: a = … b = … c = …
- Calculate the discriminant using the formula: D = b 2 − 4 ac
- If D > 0, there will be two different roots, which are found by the formula: x 1,2 = − b ± D 2 a
- If D = 0, there will be one root, which is found by the formula: x = − b 2 a
- If D < 0, there are no solutions: x ∈ ∅
Examples of solving a quadratic equation:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 ac = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – there will be two different roots:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Answer: x 1 = − 1, x 2 = 7
- − x 2 + 4 x − 4 = 0
a = − 1, b = 4, c = − 4
D = b 2 − 4 ac = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – there will be one root:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
Answer: x = 2
- 2 x 2 − 7 x + 10 = 0
a = 2, b = − 7, c = 10
D = b 2 − 4 ac = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D < 0 – there are no solutions.
Answer: x ∈ ∅
There are also incomplete quadratic equations (these are quadratic equations in which either b = 0, or c = 0, or b = c = 0). Watch the video on how to solve these quadratic equations!
The square trinomial can be factored as follows:
ax 2 + bx + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
where a is a number, a coefficient before the leading coefficient,
x – variable (i.e. letter),
x 1 and x 2 are numbers, roots of the quadratic equation ax 2 + bx + c = 0, which are found through the discriminant.
If a quadratic equation has only one root, then the expansion looks like this:
ax 2 + bx + c = a ⋅ ( x − x 0 ) 2
Examples of factoring a quadratic trinomial:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
If the quadratic trinomial is incomplete, ( ( b = 0 or c = 0 ) then it can be factored in the following ways:
- c = 0 ⇒ ax 2 + bx = x ( ax + b )
- b = 0 ⇒ apply the abbreviated multiplication formula for the difference of squares.
Let f(x) and g(x) be some functions depending on the variable x.
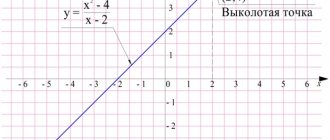
A fractional rational equation is an equation of the form f ( x ) g ( x ) = 0 .
In order to solve a fractional rational equation, we need to remember what a ODZ is and when it occurs.
ODZ is the range of permissible values of a variable.
In an expression like f(x) g(x) = 0
ODZ: g ( x ) ≠ 0 (the denominator of the fraction cannot be equal to zero).
Algorithm for solving a fractional rational equation:
- Reduce the expression to the form f ( x ) g ( x ) = 0 .
- Write out the ODZ: g ( x ) ≠ 0.
- Equate the numerator of the fraction to zero f ( x ) = 0 and find the roots.
- Indicate in your answer the roots from the numerator, excluding those roots that fall into the ODZ.
An example of solving a fractional rational equation:
Solve the fractional rational equation x 2 − 4 2 − x = 1.
Solution:
We will act in accordance with the algorithm.
- Reduce the expression to the form f ( x ) g ( x ) = 0 .
We move the unit to the left side, write an additional factor to it to bring both terms to one common denominator:
x 2 − 4 2 − x − 1 \ 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
The first step of the algorithm was completed successfully.
- Write out the ODZ:
g(x) ≠ 0
2 − x ≠ 0
− x ≠ − 2
x ≠ 2
We frame the ODZ, do not forget about it: x ≠ 2
- Equate the numerator of the fraction to zero f ( x ) = 0 and find the roots:
x 2 + x − 6 = 0 – Quadratic equation. We solve through the discriminant.
a = 1, b = 1, c = − 6
D = b 2 − 4 ac = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – there will be two different roots.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
[ x 1 = 2 x 2 = − 3
- Indicate in your answer the roots from the numerator, excluding those roots that fall into the ODZ.
Roots obtained in the previous step:
[ x 1 = 2 x 2 = − 3
ODZ: x ≠ 2
This means that the answer contains only one root, x = − 3.
Answer: x = − 3.
A system of equations is two equations with two unknowns (usually the unknowns are denoted x and y), which are combined into a common system by a curly brace.
Example of a system of equations
{ x + 2 y = 8 3 x − y = − 4
Solve a system of equations - find a pair of numbers x and y, which, when substituted into the system of equations, form a true equality in both equations of the system.
There are two methods for solving systems of linear equations:
- Substitution method.
- Addition method.
Algorithm for solving a system of equations using the substitution method:
- Express one variable in terms of another from any equation.
- Substitute the resulting value into another equation instead of the expressed variable.
- Solve an equation with one unknown.
- Find the remaining unknown.
Example:
Solve a system of equations using the substitution method
{ x + 2 y = 8 3 x − y = − 4
Solution:
- Express one variable in terms of another from any equation.
{ x = 8 − 2 y 3 x − y = − 4
- Substitute the resulting value into another equation instead of the expressed variable.
{ x = 8 − 2 y 3 x − y = − 4
{ x = 8 − 2 y 3 ( 8 − 2 y ) − y = − 4
- Solve an equation with one unknown.
3 ( 8 − 2 y ) − y = − 4
24 − 6 y − y = − 4
− 7 y = − 4 − 24
− 7 y = − 28
y = − 28 − 7 = 28 7 = 4
y=4
- Find the remaining unknown.
y=4
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
The answer can be written in one of three ways:
Answer:
- x = 0, y = 4
- { x = 0 y = 4
- ( 0 ; 4 )
Solving a system of equations using the addition method.
The addition method is based on the following property:
If
{ a = bc = d
That
(a + c) = (b + d)
The idea behind the addition method is to get rid of one of the variables by adding the equations together.
Example:
Solve a system of equations using the addition method
{ x + 2 y = 8 3 x − y = − 4
Let's get rid of the x variable in this example. The essence of the method is to have opposite coefficients in front of the variable x in the first and second equations. In the second equation, x is preceded by a coefficient of 3. In order for the addition method to work, the variable x must have a coefficient (− 3) in front of it. To do this, multiply the left and right sides of the first equation by (−3).
{ x + 2 y = 8 | ⋅ ( − 3 ) 3 x − y = − 4
{ ( − 3 ) ⋅ ( x + 2 y ) = ( − 3 ) ⋅ 8 3 x − y = − 4
{ − 3 x − 6 y = − 24 3 x − y = − 4
Now that the variable in both equations has opposite coefficients in front of it, when adding the left-hand sides of the equations, the variable x will disappear.
{ − 3 x − 6 y = − 24 3 x − y = − 4 ⊕
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
− 7 y = − 28
y = − 28 − 7 = 28 7 = 4
It remains to find the variable x. To do this, we substitute y = 4 into any of the two equations of the system. For example, the first one.
x + 2 y = 8
x + 2 ⋅ 4 = 8
x + 8 = 8
x = 8 − 8 = 0
The answer can be written in one of three ways:
Answer:
- x = 0, y = 4
- { x = 0 y = 4
- ( 0 ; 4 )
Substitution method
The substitution method is as follows: take any of these equations and express $y$ in terms of $x$, then $y$ is substituted into the system equation, from where the variable $x is found.$ After this, we can easily calculate the variable $y.$
Example 1
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {3x-y=-9} \end{array} \right.\] Let us express $y$ from the second equation through $ x$:
\[y=3x+9\]
Let's substitute into the first equation and find $x$:
\[2x+9x+27=5\] \[11x=-22\] \[x=-2\]
Let's find $y$:
\[y=-6+9=3\]
Answer: $(-2,\ 3)$
Finished works on a similar topic
- Course work Systems of equations with two variables, methods of solution 470 rub.
- Abstract Systems of equations with two variables, methods of solution 270 rub.
- Test work Systems of equations with two variables, methods of solution 190 rub.
Receive completed work or specialist advice on your educational project Find out the cost