Problems to solve independently
Problem 1. One bag contains kg of sweets, and the other contains kg.
less. What is the mass of the two packages together ? Solution
Answer: the mass of two bags together is 1 kg 300 g
Show solution
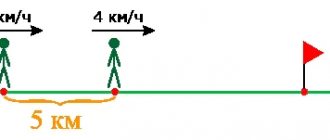
Task 2. To visit the theater, Tanya needed . It took her an hour to travel there and back. How long did the theatrical performance last?
Solution
Second way
Answer: The theatrical performance lasted 2 hours and 10 minutes.
Show solution
Problem 3. In the first hour the skier covered the entire distance that he had to cover, in the second the entire distance, and in the third the remaining part of the path. What part of the total distance did the skier cover in the third hour?
Solution
Let us determine the part of the path covered by the skier in two hours of movement. To do this, we add the fractions expressing the paths traveled in the first and second hours:
Let us determine the part of the path covered by the skier in the third hour. To do this, from all parts we subtract part of the path traveled during the first and second hours of movement:
Answer: in the third hour the skier covered the entire distance.
Show solution
Task 4. All the boys in the class took part in school competitions: some were on the football team, some on the basketball team, some competed in the long jump, and the rest of the class competed in running. What percentage of runners were more (or fewer) than football players? basketball players?
Solution
Let's determine the part of schoolchildren who participated in football, basketball and jumping:
Let's determine the part of schoolchildren who participated in the run:
Let's find out how many runners there are more (or less) than football players. First let's compare the fractions and
It was necessary to find out what percentage of runners there are more (or fewer) than football players. We found out that there are fewer runners than football players. Let's find out which part of them is smaller:
There are fewer runners than football players by a fraction.
Now we’ll find out what proportion of runners are more (or less) than basketball players. First let's compare the fractions and
It was necessary to find out what proportion of runners are more (or less) than basketball players. We found out that there are more runners than basketball players. Let's find out which part of them is larger:
There are more runners than basketball players by a fraction.
Answer: there were some fewer runners than football players and some more than basketball players.
Show solution
Task 5. The exhibition of artistic works presents painting, sculpture and graphics. All works are sculpture, painting, and the rest are graphics. What part of all work is graphics?
Solution
Let's add the fractions expressing sculpture and painting:
Let's determine what part of all work is graphics:
Answer: all work is done by graphics.
Show solution
Problem 6. Workers repaired a road 820 m long in three days. On Tuesday they repaired this road, and on Wednesday the remaining part. How many meters of road did the workers repair on Thursday?
Solution
Let's determine the length of the road repaired on Tuesday:
820: 5 × 2 = 328 m
Let's determine the length of the road repaired on Wednesday. It is known that on this day workers repaired the remaining road. The remaining road is 820−328, that is, 492
492: 3 × 2 = 328 m
Let's determine the length of the road repaired on Thursday. To do this, subtract from 820 the lengths of roads repaired on Tuesday and Wednesday:
820 − (328 + 328) = 820 − 656 = 164 m
Answer: On Thursday, workers repaired 164 meters of the road.
Show solution
Task 7. There are three stories in the book. Natasha read the first story in an hour, she spent an hour more reading the second story, and reading the third story took an hour less than reading the first and second stories together. How long did it take Natasha to read the entire book?
Solution
Let's determine the time it took Natasha to read the first story. She read it in a third of an hour. A third of an hour is 20 minutes
60: 3 × 1 = 20 minutes
Let's determine the time it took Natasha to read the second story. She expected him to be an hour longer. an hour is 10 minutes. Add 10 minutes to 20 minutes to get the reading time for the second story:
20 + 10 = 30 minutes
Let's determine the time it took Natasha to read the third story. She read it in an hour less than reading the first and second stories together. an hour is 35 minutes. Subtract 35 from the time spent reading the first and second story together (50 m)
50 − 35 = 15 m
Let's determine how long it took Natasha to read the entire book:
20 + 30 + 15 = 65 minutes = 1 hour 5 minutes
It took Natasha 1 hour and 5 minutes to read the entire book. Let's solve this problem using fractions. This way you can shorten it significantly:
this is one whole hour and an hour, and one twelfth of an hour is 5 minutes.
Answer: it took Natasha
Show solution
Problem 8. From one ton of raw cotton, 3400 m of fabric, 1.05 quintals of edible oil and 0.225 tons of cake can be produced. How many meters of fabric, edible oil and cake can be obtained from 32.4 quintals of raw cotton?
Solution
Let's convert 32.4 c into tons. One ton is 10 quintals. To find out how many ten centners (meaning tons) are in 32.4 centners, you need to divide 32.4 by 10
32.4 : 10 = 3.24 t
Let's determine how many meters of fabric can be obtained from 3.24 tons of raw cotton. From one ton, as indicated in the problem, 3400 meters of fabric are obtained. And from 3.24 tons 3.24 times more fabric will be obtained
3400 × 3.24 = 11016 meters of fabric.
Let's determine how much edible oil can be obtained from 3.24 tons of raw cotton. From one ton, as indicated in the problem, 1.05 quintals of edible oil is obtained. And from 3.24 tons 3.24 times more oil will be obtained
1.05 × 3.24 = 3.402 quintals edible oil
Let's determine how much cake can be obtained from 3.24 tons of raw cotton. From one ton, as indicated in the problem, 0.225 tons of cake is obtained. And from 3.24 tons, 3.24 times more cake will be obtained
0.225 × 3.24 = 0.729 tons of cake
Answer: from 32.4 quintals of raw cotton, 11016 meters of fabric, 3.402 quintals of edible oil and 0.729 tons of cake can be obtained.
Show solution
Problem 9. How far did the tourists go if 0.2 of the total path is 12 km?
Solution
Knowing that 0.2 of the entire path is 12 km, we can find the entire path. To find an unknown number using a decimal fraction, you need to divide the known number by the decimal fraction
12: 0.2 = 60 km
Answer: The tourists walked 60 km.
Show solution
Problem 10. Mikhail read 0.7 books, which amounted to 56 pages. How many pages are there in the book? How many pages are left to read?
Solution
Knowing that 0.7 of a book is 56 pages, we can find out how many pages there are in the book. To find an unknown number using a decimal fraction, you need to divide the known number by the decimal fraction
56 : 0.7 = 80 (total pages)
Let's find out how much time is left to read
80 − 56 = 24 (pages left to read)
Answer: the book has 80 pages. There are still 24 pages left to read.
Show solution
Problem 11. The buildings in the city are residential buildings. of which are multi-storey. What proportion of all buildings in the city are multi-storey residential buildings?
Solution
We divide residential buildings into three parts:
Now, multi-storey buildings account for a third of all buildings. Initially, all buildings were divided into three equal parts. They are now divided into nine equal parts. Residential buildings, which were previously expressed as a fraction, are now expressed as a fraction
To find out how many multi-story buildings account for two-thirds, multiply by 2
Answer: residential multi-storey buildings make up all the buildings in the city.
Show solution
Problem 12. From a rope whose length is m, you need to cut m. How to do this without making measurements?
Solution
Let us schematically depict one meter of rope:
Let us highlight the meters in this figure:
Here we highlight the meters
There was one piece left unselected. Let's find out what this piece is. To do this, subtract from
m is the part of the rope that needs to be cut. Then we get m of rope.
Now it remains to find out how many times m contains m
This means that in order to cut off m of rope without taking measurements, you need to fold this rope in four and cut off one part. The remaining part will be half of one meter.
Answer: in order to cut m from a rope whose length is m, you need to fold this rope in four and cut off one part from it. The remaining part will become m of rope.
Show solution
Did you like the lesson? Join our new VKontakte group and start receiving notifications about new lessons
Do you want to support the project? Use the button below
Published by Author
Optional course “Solving word problems” (grade 6)
The mathematics course program for 6th grade students is aimed at expanding and deepening knowledge in the subject and is developed in accordance with the interests of students and their capabilities. The course program includes information that is not included in the basic curriculum of the basic school, but is necessary for solving problems of an increased level of complexity.
- . Planned results of studying the course
Students will learn:
- reason when solving logical problems, problems of ingenuity, problems of erudition and intuition;
- will form an idea of methods and techniques for solving arithmetic and geometric problems; including non-standard
- transfer knowledge and skills to a new, non-standard situation.
- systematize data in the form of tables when solving problems, when composing mathematical crosswords, charades and puzzles;
- will expand knowledge in the field of the history of the development of mathematical science, biographies of famous mathematicians.
Students will have the opportunity to learn:
- develop mathematical outlook, thinking, research skills
- work in the information field (tables, diagrams, diagrams, graphs, sequences, chains, aggregates); present, analyze and interpret data;
- apply the learned methods to solving Olympiad problems
- Subject content
| № p/p | Section name | Content | Number of hours per program |
| I | Number systems | Decimal number system (1h). Binary number system (3h). Octal number system (2h) | 7 |
| II | II Divisibility of numbers | Signs of divisibility by 4,6,7,8,11. (3 hours) Finding GCD and LCM using the Euclidian method (2 hours). Solving problems on finding the LCM and GCD of numbers (2 hours) | 8 |
| III | Proportions, percentages, teamwork | Proportions (2 hours). Problems on percentages (2 hours). Problems on joint work (3 hours). | 7 |
| IV | Elements of combinatorics and probability theory | Rearrangements (1 hour). Samples (1 hour). Accommodation (1 hour). Combinations (1 hour). Random events (1h). Class of a certain probability of events (2h). | 7 |
| V | Problem solving | Ararithmetic of remainders. Coordinate plane. Mathematical models. | 5 |
| Total | 34 h |
- Calendar and thematic planning
| No. | Number of lessons | the date of the | Form of conduct | Lesson topic |
| Number systems 7h | ||||
| 1 | 1 | Lecture, work with reference literature | Decimal number system | |
| 2 | 1 | combined | Binary number system | |
| 3 | 1 | Workshop | Converting from binary number system to decimal number system | |
| 4 | 1 | Workshop | Practical lesson on converting to binary number system | |
| 5 | 1 | combined | Octal number system | |
| 6 | 1 | Workshop | Converting from octal to decimal number system | |
| 7 | 1 | Work in groups. | Final lesson “Calculus systems” | |
| Divisibility of numbers 8h | ||||
| 8 | 1 | Lesson - research | Tests for divisibility by 4,6,8 | |
| 9 | 1 | Lesson - research | Signs of divisibility by 7 and 11, 13 | |
| 10 | 1 | Lesson - research | Signs of divisibility by 2-11 | |
| 11 | 1 | Seminar | Finding GCD according to Euclid | |
| 12 | 1 | Practical work | Finding GCD and LCM numbers | |
| 13 | 1 | Practical work | Solving problems using LOC and GCD | |
| 14 | 1 | Practical work | Solving problems using LOC and GCD | |
| 15 | 1 | Work in groups. | Final lesson on the topic of divisibility of numbers | |
| Proportions, percentages, teamwork 7 hours | ||||
| 16 | 1 | Workshop | Proportions | |
| 17 | 1 | Workshop | Problems on proportions | |
| 18 | 1 | Workshop | Interest | |
| 19 | 1 | Workshop | Percentage problems | |
| 20 | 1 | Workshop | Collaboration | |
| 21 | 1 | Workshop | Collaboration tasks | |
| 22 | 1 | Work in groups. | Final lesson on the topic “Proportions, percentages, teamwork” | |
| Elements of combinatorics and probability theory 7h | ||||
| 23 | 1 | Work in groups. | Rearrangements | |
| 24 | 1 | combined | Samples | |
| 25 | 1 | Work in groups. | Accommodation | |
| 26 | 1 | Work in groups. | Combinations | |
| 27 | 1 | combined | Random Events | |
| 28 | 1 | combined | Classic definition of event probability | |
| 29 | 1 | Workshop | Solving problems to determine the probability of events | |
| Problem solving 5h | ||||
| 30 | 1 | combined | Arithmetic of remainders | |
| 31 | 1 | Workshop | Coordinate plane | |
| 32 | 1 | Seminar, work with reference literature | Mathematical models in human practice | |
| 33 | 1 | Workshop | Arithmetic of remainders | |
| 34 | 1h | Seminar. project protection | On the role of mathematics in human practical life | |
| Total: 34 hours | ||||