Geometry lesson on the topic “Tetrahedron and its section”
Geometry lesson 10 for UMK Atanasyan L.S.
Mathematics and computer science teacher: Kalabina NN
Lesson topic: Tetrahedron and its section.
Lesson objectives:
Introduce the concept of a tetrahedron and its components,
Learn to draw a tetrahedron,
Introduce the definition of a tetrahedron section and the rules for constructing sections
Continue to develop skills in applying the axioms of stereometry and their consequences,
Develop spatial thinking and computer skills
Foster a desire to acquire new knowledge and interest in the subject
Justify and refute the proposals put forward.
Lesson equipment:
computer, projector, interactive whiteboard, presentation, mathematical constructor model 059 “Triangular Pyramid”.
During the classes
Org moment
Updating knowledge
Frontal work with the class on the topic “Properties of parallel planes” Slide 3-7 (students read the question on the slide, give an answer, confirming it with theoretical material, then a short correct answer is displayed on the slide)
What is the relative position of two planes if the third plane intersects them along straight lines: a) having a common point; b) having no common points?
The two sides of a trapezoid lie in parallel planes. Could these sides be its sides?
What can be the relative position of two lines if these lines intersect two parallel planes and their segments between the planes are not equal?
Two planes are intersected by two parallel lines. Find out the relative position of these planes, if the segments of these lines enclosed between these planes are not equal?
Line a intersects parallel planes α and β at points A and B. Line b, parallel to line a, intersects planes at points C and D. Find the perimeter of quadrilateral ABCD if AB=3cm, BC=4cm.
Learning new material
Today in the lesson we will get acquainted with a geometric body, which will give us the opportunity to illustrate concepts related to the relative position of lines and planes.
Concept of tetrahedron:
slide number 8. Tetrahedron means tetrahedron, (τετραεδρον) “tetra” means four in Greek, and “hedra” means face.
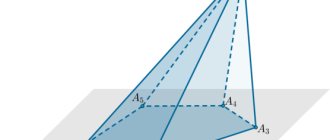
slide number 9. Consider an arbitrary triangle ABC and a point D that does not lie in the plane of this triangle. By connecting point D with segments to the vertices of triangle ABC, we obtain triangles DAB, DBC, DCA. A surface composed of four triangles ABC, DAB, DBC, DCA is called a tetrahedron and is designated DАВС.
slide No. 10 Launch the “Triangular Pyramid” model via hyperlink, a mathematical constructor to get acquainted with the elements of the tetrahedron: vertices, faces, side edges.
slide No. 11 The tetrahedron is usually depicted in the form of a convex and non-convex quadrangle with diagonals. In this case, invisible edges are depicted with dashed lines.
Assignment for students: Draw tetrahedrons in a notebook according to the sample on the slide (both methods), label them.
slide No. 12 Two edges of a tetrahedron that do not have common vertices are called opposite. Two edges of a tetrahedron that do not have common vertices are called opposite.
Assignment for students: Please name the opposite edges of the tetrahedron DABC.
The concept of a tetrahedron section:
Slide No. 13 A cutting plane of a tetrahedron is any plane on both sides of which there are points of a given tetrahedron
. The cutting plane of a tetrahedron intersects the faces of the tetrahedron along segments. A polygon whose sides are these segments is called a section of a tetrahedron.
Slide No. 14 because Since a tetrahedron has four faces, the cross-section can result in either triangles or quadrangles.
Slide No. 15 rules for constructing a section.
Consolidation of the studied material. Practical work.
Construct sections on the interactive board and in a notebook, slides No. 16, 17. Students work in workbooks, the teacher models the condition of the problem in a mathematical constructor, placing dots. The check is carried out according to the solution on the interactive board.
Lesson summary
What polyhedron did you learn about in class today?
How to construct a cross section of a tetrahedron?
What did you like? What didn't you like?
Homework:
§ 12, § 14 (1 paragraph). No. 66, No. 72.
- presentation for the lesson PPTX / 2.39 MB model triangular pyramid MKZ / 17.55 KB
Presentation for the lesson (geometry, grade 10) on the topic: Tetrahedron - presentation
MBOU "Avilovskaya Secondary School" Mathematics teacher Tkachenko I.A.
The concept of a tetrahedron A pyramid with a triangle at its base is called a triangular pyramid or tetrahedron. The word “tetrahedron” is formed from two Greek words: tetra - “four” and hedra - “base”, “face”. A tetrahedron is a polyhedron with 4 triangular faces, 6 edges and 4 vertices, at each of which 3 edges meet.
Construction of a tetrahedron A tetrahedron is usually depicted as a quadrilateral with diagonals, one of which (corresponding to an invisible edge) is depicted as a dotted line. A B C D
Tetrahedron DABC - tetrahedron A, B, C, D - vertices ABC - base AD, BD, CD, AC, AB, BC - edges AH - height of the tetrahedron CABDH Two edges of the tetrahedron that do not have common vertices are called opposite. For example, AD and BC, BD and AC, AB and CD.
Definitions of median, bimedian and altitude of a tetrahedron A segment connecting the vertex of a tetrahedron with the point of intersection of the medians of the opposite face is called its median, omitted from this vertex. The segment connecting the midpoints of the intersecting edges of a tetrahedron is called its bimedian connecting these edges. A segment connecting a vertex to a point on the opposite face and perpendicular to this face is called its height, omitted from the given vertex.
Elements of symmetry of a tetrahedron A tetrahedron has three axes of symmetry that pass through the midpoints of the intersecting edges. The tetrahedron has 6 planes of symmetry, each of which passes through an edge of the tetrahedron perpendicular to the edge that intersects with it.
Volume of the pyramid where S OCH is the area of the base, h is the height. h
Surface area of the pyramid
Types of tetrahedrons An equilateral tetrahedron is a tetrahedron in which all faces are equal triangles. An orthocentric tetrahedron is a tetrahedron in which all the heights descending from the vertices to opposite faces intersect at one point. A rectangular tetrahedron is a tetrahedron in which all the edges adjacent to one of the vertices are perpendicular to each other. A regular tetrahedron is a tetrahedron whose faces are all equilateral triangles. A commensurate tetrahedron whose biheights are equal. An incentric tetrahedron is a tetrahedron in which the segments connecting the vertices of the tetrahedron with the centers of circles inscribed on opposite faces intersect at one point.
Regular tetrahedron A tetrahedron, all four faces of which are equal regular triangles, is called a regular tetrahedron. A regular tetrahedron is a special case of a regular triangular pyramid.
All four faces of a regular tetrahedron are regular triangles. If the length of the edge of a regular tetrahedron is denoted by a, then we can calculate: Total surface area Radius of the circumscribed sphere Volume Angle of inclination of the edge Height Angle of inclination of the face Radius of the inscribed sphere Solid angle at the vertex Regular tetrahedron
Rectangular tetrahedron A tetrahedron in which three right angles meet at one vertex is called a rectangular tetrahedron. Such a tetrahedron can be obtained by cutting a cube.
Tetrahedrons in living nature Some fruits, four of them on one hand, are located at the vertices of a tetrahedron that is close to regular. This design is due to the fact that the centers of four identical balls touching each other are located at the vertices of a regular tetrahedron. Therefore, ball-like fruits form a similar relative arrangement. For example, walnuts can be arranged in this way.
Tetrahedra in construction A tetrahedron forms a rigid, statically definable structure. A tetrahedron made of rods is often used as a basis for spatial load-bearing structures of building spans, floors, beams, trusses, bridges, etc. The rods experience only longitudinal loads.
Tetrahedron in optics The rectangular tetrahedron is used in optics. If the right-angled faces are coated with a reflective compound, or the entire tetrahedron is made of a highly refractive material to create the effect of total internal reflection, then light directed at the face opposite the right-angled vertex will be reflected in the same direction from which it came. . This property is used to create corner reflectors and reflectors.
Tetrahedra in the microcosm Methane molecule CH 4 Ammonia molecule NH 3 Diamond C tetrahedron with an edge equal to 2.5220 angstroms Fluorite CaF2, tetrahedron with an edge equal to 3.8626 angstroms Sphalerite, ZnS, tetrahedron with an edge equal to 3.823 angstroms Complex ions [BF4] -, [ ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+ Silicates whose structures are based on the silicon-oxygen tetrahedron 4-
Tetrahedra in production The tetrahedron shape cannot be called convenient, but it also has applications, for example, in the manufacture of milk bags. It turned out that it is convenient to glue such tetrahedrons together on a conveyor belt by cutting blanks for them from a cardboard hose.
G10(I)-4. Tetrahedron and parallelepiped
Geometry 10th grade. Chapter I. _ Test 4.
Option 1.
1. Choose the correct statements.
1) The faces of a tetrahedron are the triangles that make up the tetrahedron.
2) Parallelepiped ABCDA1B1C1D1 is a surface composed of two equal rectangles ABCD and A1B1C1D1 and four rectangles AA1D1D, DD1C1C, BB1C1C and AA1B1B.
3) The diagonal of a parallelepiped is a segment connecting two vertices of any face.
4) The cross-section of a tetrahedron can only be triangles and quadrangles, since a tetrahedron has 4 faces.
5) The diagonals of a parallelepiped intersect at one point and are bisected by this point.
A ) 1; 3; 4; B ) 1; 2; 3; C ) 1; 3; 5; D ) 1; 4; 5.
2. Name all pairs of crossing edges of the MPEK tetrahedron in Figure 1.
A) MP and KE; MK and PE; ME and PK; B) MP and PE; MK and PE; ME and PK;
C) MP and KE; MK and KE; ME and PK; D ) MP and KE; MK and PE; ME and EK.
3. Select the correct statements using Figure 2.
1) X – the point of intersection of straight line ME and plane ABC.
2) P – the point of intersection of the straight line EK and the plane ABD.
3) Points X and P lie in the same plane.
A ) 2 and 3; B ) 1 and 3; C ) 1 and 2; D ) 1; 2 and 3.
4. In Figure 3, point M belongs to the side face CC1D1D of the rectangular parallelepiped ABCDA1B1C1D1. Through point M, draw a section of the parallelepiped with a plane parallel to plane ABC. Find the area of this section if AB=5 cm, AD=7 cm, AA1=9 cm.
A ) 45 cm2; B ) 35 cm2; C ) 63 cm2; D ) 21 cm2.
5. The base of the parallelepiped ABCDA1B1C1D1 in Figure 4 is a square with a side of 10 cm and a side edge of 12 cm. Angle B1BD is a right angle. Draw a section of the parallelepiped through points B, D and B1 and find the area of this section.
6. Redraw Figure 5 in your notebook and draw a section of the parallelepiped through points B1, D1 and M. What figure is obtained in the section?
A ) triangle; B ) quadrilateral; C ) pentagon; D ) hexagon.
Option 2.
1. Choose the correct statements.
1) A surface made up of four triangles is called a tetrahedron.
2) Two edges of a tetrahedron that do not have common vertices are called adjacent.
3) The faces of a parallelepiped are the parallelograms from which the parallelepiped is composed.
4) The cutting plane of a parallelepiped is any plane on both sides of which there are points of a given parallelepiped.
5) Two faces of a parallelepiped that have common edges are called opposite.
A ) 1; 3; 4; B ) 1; 2; 3; C ) 1; 3; 5; D ) 1; 4; 5.
2. Name all pairs of crossing edges of the KABM tetrahedron in Figure 1.
A) AK and AB; B.K. and A.M.; MK and AB; B ) AK and BM; BK and AB; MK and AB;
C ) AK and BM; B.K. and A.M.; MK and AB; D ) AK and BM; B.K. and A.M.; MK and MB.
3. Select the correct statements using Figure 2.
1) P – the point of intersection of the straight line AB and the NMQ plane.
2) E – the point of intersection of straight line AC and plane MFQ.
3) Points E and P lie in different planes.
A ) 1; 2 and 3; B ) 1 and 3; C ) 1 and 2; D ) 2 and 3.
4. In Figure 3, point M belongs to the side face CC1D1D of the rectangular parallelepiped ABCDA1B1C1D1. Through point M, draw a section of the parallelepiped with a plane parallel to the plane AA1D1. Find the area of this section if AB=5 cm, AD=7 cm, AA1=9 cm.
A ) 45 cm2; B ) 35 cm2; C ) 63 cm2; D ) 21 cm2.
5. The base of the parallelepiped ABCDA1B1C1D1 in Figure 4 is a square with a side of 8 cm and a side edge of 7 cm. Angle B1BD is a right angle. Draw a section of the parallelepiped through points B, D and D1 and find the area of this section.
6. Redraw Figure 5 in your notebook and draw a section of the parallelepiped through points M, P and T. What figure is obtained in the section?
A ) triangle; B ) quadrilateral; C ) pentagon; D ) hexagon.
Option 3.
1. Choose the correct statements.
1) A tetrahedron has 4 faces, 6 edges and 4 vertices.
2) The parallelepiped has 6 faces, 12 edges and 8 vertices.
3) The opposite faces of the parallelepiped are parallel and equal.
4) A cutting plane of a tetrahedron is any plane on one side of which there are points of a given tetrahedron.
5) The cutting plane intersects the faces of the parallelepiped along the edge segments of the parallelepiped. The polygon whose sides are these segments is called a section of a parallelepiped.
A ) 1; 3; 4; B ) 1; 2; 3; C ) 1; 3; 5; D ) 1; 4; 5.
2. Select the correct statements using Figure 1.
1) M – the point of intersection of straight line AP and plane A1B1C1.
2) K – the point of intersection of straight line PF and plane ABD.
3) Points M and K lie in the same plane.
A ) 1; 2 and 3; B ) 1 and 3; C ) 2 and 3; D ) 1 and 2.
3. In the tetrahedron DABC in Figure 2, angle ADB is 60°, angles ACB and CBD are right, AD=BD, AB=26, DC=31. Find AC. Write down the square of the resulting value in your answer.
A ) 391; B ) 625; C ) 380; D ) 576.
4. The base of the parallelepiped ABCDA1B1C1D1 in Figure 3 is a square with a side of 4 cm and a side edge of 6 cm. Angle B1BD is a right angle. Draw a section of the parallelepiped through line AC parallel to B1D and find the area of this section.
5. In the tetrahedron MABC in Figure 4, a section of the KER is drawn parallel to the face of the ВСМ. The area of the triangle ВСМ is 60 cm2. Find the area of the triangle KEP if AK : KV=7 : 3.
A ) 29.4 cm2; B ) 58.8 cm2; C ) 294 cm2; D ) 30.4 cm2.
6. Redraw Figure 5 in your notebook and draw a section of the parallelepiped through points M, P and T. What figure is obtained in the section? A ) triangle; B ) quadrilateral; C ) pentagon; D ) hexagon.
Option 4.
1. Choose the correct statements.
1) Two faces of a parallelepiped that have a common edge are called adjacent.
2) All edges of the parallelepiped are called lateral edges.
3) The cutting plane intersects the faces of the tetrahedron along straight segments containing the edges of the tetrahedron. A polygon whose sides are these segments is called a section of a tetrahedron.
4) The cross-section of a parallelepiped can be triangles, quadrangles, pentagons and hexagons, since the parallelepiped has 6 faces.
5) The diagonals of a parallelepiped intersect at one point and are bisected by this point.
A ) 1; 3; 4; B ) 1; 2; 3; C ) 1; 3; 5; D ) 1; 4; 5.
2. Select the correct statements using Figure 1.
1) P – the point of intersection of the straight line NK and the plane ACD.
2) E – the point of intersection of straight line DK and plane A1B1C1.
3) Points E and P lie in different planes.
A ) 2 and 3; B ) 1 and 3; C ) 1; 2 and 3; D ) 1 and 2.
3. In the tetrahedron DABC in Figure 2, the angles ACB, ADV and CBD are straight, AD=BD=8, DC=11. Find AC. Write down the square of the resulting value in your answer.
A ) 72; B ) 71; C ) 57; D ) 64.
4. The base of the parallelepiped ABCDA1B1C1D1 in Figure 3 is a square with a side of 6 cm and a side edge of 8 cm. Angle B1BD is a right angle. Draw a section of the parallelepiped through line AC parallel to B1D and find the area of this section.
5. In the tetrahedron DABC in Figure 4, a section MPK is drawn parallel to the face ADC. The area of triangle MRC is 4 cm2. Find the area of triangle ADC if СК : ВК = 3 : 5.
A ) 10.24 cm2; B ) 20.48 cm2; C ) 6.4 cm2; D ) 8.64 cm2.
6. Redraw Figure 5 in your notebook and draw a section of the parallelepiped through points M, P and K. What figure is obtained in the section? A ) triangle; B ) quadrilateral; C ) pentagon; D ) hexagon.
Reference materials.
1) A surface made up of four triangles is called a tetrahedron.
2) The faces of a tetrahedron are the triangles that make up the tetrahedron.
3) A tetrahedron has 4 faces, 6 edges and 4 vertices.
4) Two edges of a tetrahedron that do not have common vertices are called opposite.
5) Parallelepiped ABCDA1B1C1D1 is a surface composed of two equal parallelograms ABCD and A1B1C1D1 and four parallelograms AA1D1D, DD1C1С, BB1C1C and AA1B1B.
6) The faces of a parallelepiped are the parallelograms from which the parallelepiped is composed.
7) The parallelepiped has 6 faces, 12 edges and 8 vertices.
 Two faces of a parallelepiped that have a common edge are called adjacent.
Two faces of a parallelepiped that have a common edge are called adjacent.
9) Two faces of a parallelepiped that do not have common edges are called opposite.
10) The diagonal of a parallelepiped is a segment connecting two vertices that do not belong to the same face.
11) The edges of a parallelepiped that do not belong to the bases are called lateral edges.
12) The opposite faces of the parallelepiped are parallel and equal.
13) The diagonals of a parallelepiped intersect at one point and are bisected by this point.
14) A cutting plane of a tetrahedron is any plane on both sides of which there are points of a given tetrahedron.
15) The cutting plane of a parallelepiped is any plane on both sides of which there are points of a given parallelepiped.
16) The cutting plane intersects the faces of the tetrahedron along segments. A polygon whose sides are these segments is called a section of a tetrahedron.
17) The cutting plane intersects the faces of the parallelepiped along segments. The polygon whose sides are these segments is called a section of a parallelepiped.
18) The cross-section of a tetrahedron can only be triangles and quadrangles, since a tetrahedron has 4 faces.
19) The cross-section of a parallelepiped can be triangles, quadrangles, pentagons and hexagons, since the parallelepiped has 6 faces.
Tags: geometry 10th grade tests, polyhedra, lines and planes, stereometry