Lesson on the topic: The third sign of equality of triangles lesson plan in geometry (grade 7) on the topic

Geometry lesson notes, 7th grade. The third sign of equality of triangles

The third criterion for the equality of triangles
Author: Olga Adolfovna Opaleva, mathematics teacher, Kolyanovskaya Secondary School. I offer a summary of a geometry lesson for 7th grade students. Lesson topic: The third sign of equality of triangles Lesson type: lesson in the formation of new knowledge Purpose of the lesson: to create conditions for personal self-realization of each student in the process of studying the topic “The third sign of equality of triangles”, to promote the development of information, communication, educational, reflective, health-preserving competencies. Lesson objectives: educational: prove the third sign of equality of triangles; to develop in students the skills of using the triangle equality sign when solving developmental problems: to develop logical thinking, memory, and research qualities of students; develop the emotional sphere of students through the use of active forms of teaching lessons, including ICT; develop reflexive skills through analyzing the results of the lesson and self-analysis of one’s own achievements in it; develop speech as an indicator of the student’s intellectual and general development; educational: cultivate accuracy, accuracy, develop communication skills. Predicted result: students must: show knowledge of the material on the topic “The third criterion for the equality of triangles”; be able to solve problems using the 3rd sign of equality. Lesson plan: 1. Organizational and motivational moment - 3 min. 2. Updating knowledge – 5 min. 3. Studying new material – 14 min. 4. Consolidation of the studied material - 15 minutes 5. Summing up the lesson. Reflection. Homework - 3 min Organizational moment The teacher welcomes the students. Lesson quote: Studying and not thinking is a waste of time (Chinese wisdom) A wonderful geometric figure and the most popular in the school geometry curriculum is a triangle. Maybe you think that triangles “settled” only on the pages of a geometry textbook and can’t be seen anywhere else? Where can you find a triangle besides geometry? (The guys express their versions) Why is a triangle-shaped structure needed? Why a triangle? During the lesson we will try to answer this question. Updating knowledge Let us recall some facts familiar to us. We will solve problems orally. #1 Find the angle adjacent to the 159 degree angle. No. 2 find pairs of equal triangles (Figures 52, 53 textbook “Geometry 7-9 L.S. Atanasyan) The question of how to prove the equality of triangles is discussed. What signs are there? Which elements can be said to be equal? Studying new material At home, you were asked to build and cut out triangles: 1) with given sides. (AB=6, BC=2, AC=7). Compare it with the triangles built by your neighbors. Conclusion? (We got equal triangles.) How did you determine? (Overlay.) It seems that there is nothing surprising, the data were the same. 2) With given angles (30 degrees, 60 degrees, 90 degrees) Compare it with the triangles constructed by your neighbors. What do you notice? (We got different triangles.) What conclusion can be drawn? So, what can you and I assume? (Triangles with equal sides are equal, but with equal angles they may not be equal. That they discovered another sign of equality of triangles.) Lesson topic: The third sign of equality of triangles. Try to formulate the sign. Let’s check the formulation of the theorem. Textbook paragraph 20 But for now this statement is at the level of our assumptions. Does it apply to all triangles? To assert this, you need to prove the theorem. (The proof, according to the textbook, is carried out jointly by the teacher and students). Reinforcing the learned material In life, we encounter many practical problems that mathematics helps us solve. Task: Mom bought 1 meter of fabric 1 meter wide for a scarf for her two daughters. Divide this piece of fabric into two equal parts, make sure that your daughters do not quarrel (the scarves are equal) and prove the correctness of your actions. (Students work with a square made of paper. Fold it diagonally, you get two isosceles triangles, equal on three sides. An explanation follows from the students.) Using the accumulated experience in solving problems, solve No. 136 of the textbook yourself. Summing up the lesson. Reflection. Let's return to the question. that arose at the beginning of the lesson. Why is the triangle present in the design? From the 3rd sign it follows that a triangle is a rigid figure, unlike other geometric figures. Demonstration and explanation of the property. (Let’s imagine two slats, the two ends of which are fastened together. This design is not rigid: by moving or pushing apart the free ends of the slats, we can change the angle between them. Now let’s take another slats and fasten its ends with the free ends of the first two slats. The resulting the structure - a triangle - will already be rigid. It is impossible to move or move apart any two sides, i.e., it is impossible to change the angle. Indeed, if this were possible, then we would get a new triangle, not equal to the original one. But this is impossible. Why ? (The new triangle must be equal to the original one according to the 3rd sign of equality of triangles.) What does it consist of? Well done. Students are offered questions for reflective analysis of their activities in the lesson. What new did you learn in the lesson? What was the greatest difficulty? In what mood did you work in the lesson? lesson? Draw using a triangle lying on your desk. Homework P. 20, 136, 138 Creative task: work “In the world of triangles” (look around and find among familiar things).

We recommend watching:

Notes for a 7th grade geometry lesson on the topic “Relationships between the sides and angles of a triangle.” Notes for a 7th grade geometry lesson with presentation. Triangles Lesson notes for an integrated lesson in geometry and the Russian language with presentation, grade 7. Work program for an elective in mathematics, grade 7.

Similar articles:

Geometry lesson notes for 7th grade

Math quizzes with answers, 7th grade

The third sign of equality of triangles

Let us recall the first and second signs of equality of triangles.

The first sign of equality of triangles:

If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent.

The second sign of equality of triangles:

If a side and two adjacent angles of one triangle are respectively equal to a side and two adjacent angles of another triangle, then such triangles are congruent.

Let us formulate the third criterion for the equality of triangles

:

If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent.

Let ABC and A1B1C1 be two triangles with AB=A1B1, BC=B1C1 and CA=C1A1. Let us prove that ∆ ABC= ∆ A1B1C1.

Let us apply ∆ ABC to ∆ A1B1C1 in such a way that vertex A coincides with vertex A1, vertex B coincides with vertex B1, and vertices C and C1 are on opposite sides of straight line A1B1.

There are three possible cases.

Let's consider the first case. Since, according to the conditions of the theorem, AC = A1C1, BC = B1C1, then the triangles A1C1C and B1C1C are isosceles. According to the theorem on the property of the angles of an isosceles triangle, angle 1 is equal to angle 2, and angle 3 is equal to angle 4. Therefore, ∠A1CB1=∠A1C1B1.

We get AC=A1C1, BC=B1C1 and ∠C=∠C1. Therefore, ∆ ABC= ∆ A1B1C1 according to the first sign of equality of triangles.

Let's consider the second case. Since, according to the conditions of the theorem, AC = A1C1, then ∆ CA1C1 is isosceles. According to the theorem on the property of the angles of an isosceles triangle, the base angles C and C1 are equal. We can say that triangles ABC and A1B1C1 are equal according to the first sign of equality of triangles, since AC = A1C1 and BC = B1C1 according to the conditions of the theorem, and ∠C = ∠C1.

And the third case. According to the conditions of the theorem, AC = A1C1 and BC = B1C1. It follows from this that the triangles CA1C1 and CB1C1 are isosceles. Then, by the theorem about the property of angles at the base of an isosceles triangle, ∠1=∠2 and ∠3=∠4. And therefore, ∠С=∠С1. So, triangles ABC and A1B1C1 are equal according to the first sign of equality of triangles, since AC = A1C1 and BC = B1C1 according to the conditions of the theorem, and ∠C = ∠C1.

The theorem has been proven.

Example.

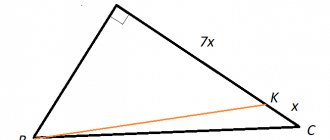
Segment AC is the common base of isosceles triangles ABC and ADC. Prove that triangles BAD and BCD are congruent.

Consider ∆ BAD and ∆ BCD. These triangles have side AB=BC, side AD=DC, and side BD is common.

We find that triangles BAD and BCD are equal according to the third criterion for the equality of triangles. Q.E.D.

Example.

Two equal segments AB and CD intersect at point E so that the distances AD and CB are equal. Prove that AE=CE.

Let's connect points A and C. And consider ∆ ABC and ∆ CAD. Their side AC is common, AB = CD according to the condition, AD = CB also according to the condition of the problem. Then triangles ABC and CAD are equal according to the third criterion.

From the equality of triangles it follows that ∠1=∠2.

By connecting points B and D, we can similarly prove that triangles CBD and ADB are equal, and therefore angles 3 and 4 are equal.

Then we can say that ∆ CEB=∆ AED according to the second criterion, since they have ∠1=∠2, ∠3=∠4, and the sides AD and CB are equal according to the conditions of the problem. Therefore, we find that side AE ​​= CE. Q.E.D.

Consider the property of a triangle, which follows from the third criterion for the equality of triangles:

Let's take two slats, the two ends of which are fastened together. If we move and move apart the free ends of these slats, the angle between them will change. But if we take the third slats and fasten its ends with the free ends of the first two slats, then we will no longer be able to move or move apart any two sides, which means we cannot change a single angle.

Since a triangle has this property, it is called a rigid figure.

.

This property of the triangle makes it indispensable in technology and construction. The triangle-shaped structural elements retain their shape.

For example, to secure a pole in a vertical position, a support is placed on it. The bracket is installed using the same principle.

And also the stepladder posts can move freely if they are not secured with a jumper.

Lesson “The third criterion for the equality of triangles”

Lesson topic: The third criterion for the equality of triangles

Type: lesson on learning new material

Goals: to prove the third sign of equality of triangles, to develop the ability to use the studied material to solve geometric problems.

Tasks:

Educational:

repetition of the concepts of an isosceles triangle, its properties and characteristics, median, height, bisector of a triangle, creating conditions for students to “discover” the third sign of equality of triangles; developing problem solving skills using learned theorems.

Educational:

development of thinking, attention, memory; broadening one's horizons; formation of a culture of mathematical speech and writing.

Educational:

nurturing skills to work in pairs and in a team, developing independence, responsibility, nurturing cognitive interest in studying the subject.

Educational and methodological support:

1. Kazakov V.V. Geometry: textbook. manual for 7th grade institutions general. avg. education with Russian language of instruction / V.V. Kazakov. – Minsk: People's Asveta, 2017
2. Computer presentation “The third sign of equality of triangles”
3. “Repetition” cards (Appendix 1)

During the classes

1. Organizing time

Greeting students. Checking readiness for class.

1. Checking homework

To check the solution to problems No. 100 (b, c) and No. 101 [1]

The “Question Chain” technique is used. Brief conditions of the tasks and pictures for them are displayed on the screen. One of the students comments on the solution to the problem; at any point in his answer he is interrupted by the teacher, and the other student continues the solution.

1. Updating students' knowledge and skills. Repetition

Work in pairs using “Repetition” cards. Students perform 1–3 tasks orally, then their answers are checked using a presentation.

1. Setting lesson goals and objectives

Communicate the lesson topic and goals.

1. Motivation for learning activities

When studying congruent triangles, geometers asked the question: “With the help of what elements can a triangle be uniquely determined?”

If we consider two triangles with three equal angles, they will not be equal. What if we consider triangles with equal sides? When these figures are superimposed on each other, they will coincide at the corners and sides. Let's try to prove this.

1. Learning a new topic

1. Proof of the theorem (heuristic conversation)

On the screen there are triangles ABC and A1B1C1, in which AB = A1B1, BC = B1C1, AC = A1C1. They can be applied so that they coincide along the segment AC (A1C1). Let's draw segment BB1. Isosceles triangles BAB1 and BSV1 are considered; their angles at the bases are highlighted in different colors in the figure. Next is the conclusion about equal angles B and B1. This means that ABC and A1B1C1 are equal on both sides and the angle between them.

1. Students write this theorem in a notebook in the form of a supporting note.

1. Practical significance of the theorem.

Three sides define a triangle uniquely. A triangle is a rigid figure. This corollary of the theorem is widely used in the manufacture of structures that must be stable and durable.

1. Physical education minute.
2. Consolidation of what has been learned.

Complete tasks No. 108 (b, d), No. 111, test (p. 76) from the textbook [1]

P.76, test

– independently (write down only the answer)

Problem No. 108 (b, d)

Students in pairs discuss the solution to the problem and write down the answers.

Problem No. 111

Task No. 1

(additionally)

1. Lesson summary. Reflection on students' activities.

Several students take turns repeating the basic concepts and theorems covered in class.

When summarizing the lesson and reflecting on the students’ activities, the “Pencil notes in the margins” technique is used. In the margins of the notebook opposite the notes on theoretical material or problem solving, each student writes with a pencil one of the letters - “L”, “T” or “S”. Letter designations: “L” - easy, “T” - difficult, “S” - doubts.

1. Information about homework.

• Learn the third criterion for the equality of triangles, know the proof of the theorem.
• Solve problems in writing: No. 108 (a, c), No. 112.

Annex 1

Summary of a geometry lesson in 7th grade with presentation. Signs of equality of triangles

Geometry lesson in 7th grade on the topic “Triangles.
Signs of equality of triangles." Abstract with presentation Author: Lyudmila Vasilievna Bitkova, first category mathematics teacher, municipal budgetary educational institution "Forest Basic Secondary School", Lesnoy village of Zubovo - Polyansky district of the Republic of Mordovia. Description of the material: The summary of the presented lesson is a general lesson on the topic “Triangles. Signs of equality of triangles." The purpose of the lesson is to update the material covered and activate it. The lesson allows students to deepen their knowledge of geometry and instills interest in such a serious and at the same time interesting subject. This lesson will be useful for teachers teaching geometry in the 7th grade. The lesson is accompanied by a computer presentation. Lesson topic: “Triangles. Signs of equality of triangles” Lesson objectives: 1) educational: repeat and consolidate students’ knowledge of the formulations of signs of equality of triangles; develop skills: recognize equal triangles, prove their equality, draw conclusions about the equality of some of their elements, practice problem-solving skills using signs of equality of triangles; 2) developing: develop the ability to solve problems using ready-made drawings and with a complete solution, logical thinking and cognitive activity, develop attention, auditory and visual memory, form students’ mathematical speech, as well as self-control and mutual control skills; 3) educational: to cultivate the ability to express one’s point of view, carry out reasoning and proof when solving problems, mathematical culture, the desire to actively participate in work in the lesson, as well as the ability to listen and hear one’s classmates. Lesson objectives: 1. Update basic knowledge on the topic “Triangle”. 2. Check the concept of a triangle. 3. Formulate the criteria for the equality of triangles. 4. Reinforce the material by solving problems using ready-made drawings. 5. Learn to correctly and accurately formulate and solve problems. Lesson type: lesson of generalization and systematization of knowledge, skills and abilities. Forms of work: independent, frontal, group and individual. Methods: problem-search, verbal, visual, practical. Equipment: computer, screen, multimedia projector, self-control sheets, cards with tasks for each stage of the lesson. Appendix: lesson presentation. Lesson stages: 1. Organizational moment. 2. Determining the topic and purpose of the lesson. 3. Repetition and updating of basic knowledge. 4. Application of existing knowledge when solving problems. 5. Test work with mutual verification. 6. Homework assignment. 7. Reflection.

Lesson progress:
1. Organizational moment. (3 min) Teacher: Good morning, good people! May our lesson be fruitful! Smile and sit down! Guys, this year we started studying one of the oldest and most interesting sciences - geometry. In geometry lessons we became acquainted with a geometric figure, the name of which is encrypted in the rebus: Slide 2

Correct triangle. This is a very beautiful and interesting figure that holds many secrets, like the Bermuda Triangle, in which ships and planes still disappear and no one can explain the reasons for these phenomena. If you look closely and look at the world around you, you can find many outlines of this triangle. The triangle is one of the first geometric figures that began to be used in the ornaments of ancient peoples. Even one of the constellations in the sky has the shape of a triangle. Engineers love the triangle for its strength and use it to create structures, such as the Eiffel Tower and Ostankino TV Tower, various bridges and towers. The boom of a tower crane is secured with steel ropes, forming a triangle shape (as the story progresses, you can show slides 3, 4, 5). 2. Determination of the topic and purpose of the lesson. Here is a crossword puzzle, after solving which you will repeat the definitions and find out the topic of the lesson. (5 min) Slide 6.

1. The bisector segment of an angle connecting the vertex of a triangle with a point on the opposite side is called... 2. When proving the equality of two triangles, three... triangle equalities are used. 3. What is the name of the side in an isosceles triangle that is not equal to the other two? 4. A segment connecting the vertex of a triangle with the middle of the opposite side is called... a triangle 5. What is the name of a geometric figure consisting of three points connected by segments? 6. What is the name of the perpendicular drawn from the vertex of a triangle to the line containing the opposite side? 7. What is the name of a triangle in which all sides are equal? 8. Equal sides of an isosceles triangle are called... 9. What is the name of a triangle whose two sides are equal? Assessments on the self-control sheet On your desks there are assessment sheets, where you, as always, will give yourself grades during the lesson for each type of work. Give yourself a grade for the crossword puzzle. If there are no errors – “5”, 1.2 errors – “4”, 3.4 errors – “3”, 5 or more errors – “0”. Who has “5”, “4”? Hands up. What keyword did you come up with? (equality) Slide 7.

Using the keyword, and words numbered 2 and 5, formulate the topic of the lesson. The topic of our lesson is “Signs for the equality of triangles”. Slide 8. What goals will we set?
1. Repeat the signs of equality of triangles. 2. Strengthen the ability to solve problems using these characteristics. Write down the date, class work and topic of our lesson in your notebooks. 3.Repetition and updating of basic knowledge.
1.Front survey of students (3 min). Each of you has score sheets on your desk. We will work with them throughout the lesson. For each correct answer - 1 point. 1) Formulate the first sign of equality of triangles. 2) Formulate the second criterion for the equality of triangles. 3) Which triangle is called equilateral? 4) Which triangle is called isosceles? Name the elements of an isosceles triangle. 5) Formulate the third criterion for the equality of triangles. 6) What angles are called vertical? 7) Define adjacent angles. What properties does an isosceles triangle have? 9) Which segment is called the bisector of a triangle? 10) Which segment is called the median of a triangle? 11) Which segment is called the height of the triangle? 12) Define vertical angles. — Theoretically, you are well savvy. Let's see how attentive you are. We will play a “Yes-No” game. I will hand out task cards. 2. Performing the game “Yes - No” (4 min) If the statement is correct, write “yes”, if a mistake is made, then no. Remember that in definitions and theorems there are words without which the definitions and theorems do not lose meaning, but there is a word without which the sentence does not carry any information. You are given 3 minutes to complete the task. Get started. Option 1. 1. Is it true that if the triangles are equal, then each angle of the first triangle is equal to each angle of the second triangle? (no) 2. Is it true that for each side of the first triangle you can find a side equal to it in the second, equal triangle? (yes) 3. Is it true that if the side and angle of one triangle are respectively equal to the side and angle of another triangle, then such triangles are congruent? (no) 4. Is it true that if three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent? (yes) 5. Is it true that if two angles of one triangle are respectively equal to two angles of another triangle, then such triangles are congruent? (no) Option 2. 1. Is it true that if the triangles are equal, then each side of the first triangle is equal to each side of the second triangle? (no) 2. Is it true that for each angle of the first triangle you can find an angle equal to it in the second, equal triangle? (yes) 3. Is it true that if the side and two angles of one triangle are respectively equal to the side and two angles of another triangle, then such triangles are congruent? (no) 4. Is it true that if three angles of one triangle are respectively equal to three angles of another triangle, then such triangles are congruent? (no) 5. Is it true that if two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent? (yes) - Exchange cards with your desk neighbor, check the answers, give marks with a pencil, comment on the results, correct mistakes. (Work in pairs, frontal work). The correct answers for each option are displayed on the slide. Slide 9. The testing student gives a grade according to the following criteria: 5 correct – “5”, 4 correct – “4”, 3 correct – “3”, 2 or 1 correct – “2”. Put the received mark on the evaluation sheet. — Raise your hands, those who received - 5, those who received - 4, those who received - 3. We continue to work. — Guys, for the first year you have been studying the subject of geometry and you realized that the subject of studying this section of mathematics is solving problems based on the studied definitions, properties and theorems. Slide 10. 4. Application of existing knowledge when solving problems. The famous teacher and mathematician György Pólya said: “If you want to learn to swim, then boldly enter the water, and if you want to learn to solve problems, then solve them.” (D. Polya) How do you understand these words? Task 1. Working from ready-made drawings “Continue the solution” (5 min) A drawing is depicted on the board for each row, the beginning of the solution to the problem is given, and the students of each row need to complete the solution to this problem. Students think for 1-2 minutes, deliberate in pairs, and then one representative from each row comes out and explains the solution to the problem. Slide 11.

Task 2. Oral solution of problems using ready-made drawings (6 min) We repeated how to solve problems. We solve problems orally using ready-made drawings. . ” Who is first? Slide 12 1. 2. Listen carefully as you evaluate each other. Task 3. Solving problems with complete solutions. (6 min): - In geometry, it is very important to be able to look and see, notice and note various features of geometric figures. One student solves the problem on the board, and the rest in notebooks. Slide 13 Task 1.

Task 2. Slide 14.

4. Physical education session to the music “Yellow leaves are circling over the city” (2 min) Slide 15. Inhale and exhale, stretch. Hands up, work with your fingers to form various triangles. Draw a triangle in the air with your left hand, then with your right, and then with both. Paired with a neighbor (I have two hands - two sides, the neighbor helps to make a triangle). Draw a triangle on the floor with each leg. Shake off the fatigue from your arms and legs. We sat down. 5. Test work (6 min.) Slide 16-17. For each correct answer, the participant receives 1 point. I wish you success. 1. Indicate which of the following pictures have equal triangles, by what criteria are they equal? 2. By what criteria are triangles congruent? a) on two sides and the angle between them b) on a side and two adjacent angles c) on three sides

Answers: Slide 18. 1. I, III - along two sides and the angle between them III, IV - along a side and two adjacent angles 2. According to I, the triangles in Fig. are equal. 1,4,5,8. According to the II criterion, the triangles in Fig. 3,6,9 are equal. according to the III criterion, triangles are equal 2.7 6. Homework: (1 min) (cards). Slide 19 Solve problems using ready-made drawings 1.

2.

8 Reflection. (3 min) Slide 20 Give yourself a final grade for your work in the lesson as a whole.
What did you get? Very good! What goals did we set for ourselves? Have we achieved them? Grading. You all have triangles on your tables. Those who liked our lesson and who think that they did a good job, show the green triangle; those who didn’t quite like our lesson or were less fortunate than others, show the yellow triangle. Download lesson notes on geometry in 7th grade. “Triangles. Signs of equality of triangles"

Presentation on the topic: Triangles. Signs of equality of triangles

We recommend watching:

Notes for a 7th grade geometry lesson on the topic “Relationships between the sides and angles of a triangle.” Notes for a 7th grade geometry lesson with presentation. Triangles Lesson notes for an integrated lesson in geometry and the Russian language with presentation, grade 7. Geometry lesson notes, grade 7. The third sign of equality of triangles

Similar articles:

Geometry lesson notes for 7th grade

Math quizzes with answers, 7th grade