Урок геометрии на тему «Тетраэдр и его сечение»
Урок геометрии 10 для УМК Атанасян Л.С.
Учитель математики и информатики: Калабина НН
Тема урока: Тетраэдр и его сечение.
Цели урока:
Ввести понятие тетраэдра и его составляющих,
Научить изображать тетраэдр,
Ввести определение сечения тетраэдра и правила построения сечений
Продолжить формировать навыки применения аксиом стереометрии и их следствий,
Развивать пространственное мышление, умение работать с компьютером
Воспитывать стремление к приобретению новых знаний, интерес к предмету
Обосновывать и опровергать выдвигаемые предложения.
Оборудование урока:
компьютер, проектор, интерактивная доска, презентация, математический конструктор модель 059 «Треугольная пирамида».
Ход урока
Орг момент
Актуализация знаний
Фронтальная работа с классом по теме «Свойства параллельных плоскостей» Слайд 3-7 (учащиеся читают вопрос на слайде, дают ответ, подтверждая его теоретическим материалом, далее на слайде высвечивается краткий правильный ответ)
Каково взаимное расположение двух плоскостей, если третья плоскость пересекает их по прямым: а) имеющим общую точку; б) не имеющим общих точек?
Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть ее боковыми сторонами?
Каким может быть взаимное расположение двух прямых, если эти прямые пересекают две параллельные плоскости, и их отрезки, заключенные между плоскостями, не равны?
Две плоскости пересечены двумя параллельными прямыми. Выясните взаимное расположение этих плоскостей, если отрезки данных прямых, заключенные между этими плоскостями не равны?
Прямая а пересекает параллельные плоскости α и β в точках А и В. Прямая b, параллельная прямой а, пересекает плоскости в точках C и D. Найдите периметр четырехугольника ABCD, если АВ=3см, ВС=4см.
Изучение нового материала
Сегодня на уроке мы познакомимся с геометрическим телом, которое даст нам возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей.
Понятие тетраэдра:
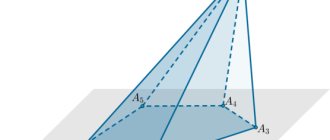
слайд №8. Тетраэдр – означает четырехгранник,( τετραεδρον) «tetra»- по -гречески четыре, а «hedra» -грань.
слайд №9. Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС получим треугольники DАВ, DВС, DСА. Поверхность, составленная из четырех треугольников АВС, DАВ, DВС, DСА, называется тетраэдром и обозначается DАВС.
слайд №10 Запуск по гиперссылке модели «Треугольная пирамида» математического конструктора для знакомства с элементами тетраэдра: вершины, грани, боковые ребра.
слайд №11 Тетраэдр изображается обычно в виде выпуклого и невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра
Задание учащимся: Начертите по образцу на слайде тетраэдры в тетради (оба способа), обозначьте их.
слайд №12 Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
Задание учащимся: Назовите, пожалуйста, противоположные ребра тетраэдра DАВС.
Понятие сечения тетраэдра:
Слайд №13 Секущей плоскостью тетраэдра называется любая плоскость, по обе стороны от которой имеются точки данного тетраэдра
. Секущая плоскость тетраэдра пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки называется сечением тетраэдра.
Слайд №14 т.к. у тетраэдра четыре грани, то в сечении могут получаться либо треугольники, либо четырехугольники.
Слайд №15 правила построения сечения.
Закрепление изученного материала. Практическая работа.
Построить сечения на интерактивной доске и в тетради слайды №16, 17. Учащиеся работают в рабочих тетрадях, учитель моделирует условие задачи в математическом конструкторе, расставляя точки. Проверку выполняют по решению на интерактивной доске.
Итог урока
С каким многогранником познакомились сегодня на уроке?
Как построить сечение тетраэдра?
Что понравилось? Что не понравилось?
Домашнее задание:
§ 12, § 14 (1 абзац).№ 66, №72.
- презентация к уроку PPTX / 2.39 Мб модель треугольная пирамида MKZ / 17.55 Кб
Презентация к уроку (геометрия, 10 класс) по теме: Тетраэдр — презентация
МБОУ «Авиловская СОШ» Учитель математики Ткаченко И.А.
Понятие тетраэдра Пирамида, в основании которой лежит треугольник, называется треугольной пирамидой или тетраэдром. Слово «тетраэдр» образовано из двух греческих слов: tetra — «четыре» и hedra — «основание», «грань». Тетраэдр — многогранник, имеющий 4 треугольные грани, 6 рёбер и 4 вершины, в каждой из которых сходятся 3 ребра.
Построение тетраэдра Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают пунктирно. А В С D
Тетраэдр DАВС – тетраэдр А, В, С, D – вершины АВС – основание АD, ВD, СD, АС, АВ, ВС– ребра АH – высота тетраэдра C A B D H Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Например, АD и ВС, ВD и АС, АВ и СD.
Определения медианы, бимедианы и высоты тетраэдра Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Элементы симметрии тетраэдра Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер. Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.
Объем пирамиды где S ОСН — площадь основания, h — высота. h
Площадь поверхности пирамиды
Типы тетраэдров Равногранный тетраэдр – это тетраэдр, у которого все грани – равные между собой треугольники. Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой. Правильный тетраэдр – это тетраэдр, у которого все грани равносторонние треугольники. Соразмерный тетраэдр, бивысоты которого равны. Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Правильный тетраэдр Тетраэдр, все четыре грани которого равные правильные треугольники, называется правильным тетраэдром. Правильный тетраэдр это частный случай правильной треугольной пирамиды.
Все четыре грани правильного тетраэдра – правильные треугольники. Если длину ребра правильного тетраэдра обозначить a, то можно вычислить: Площадь полной поверхности Радиус описанной сферы ОбъемУгол наклона ребра Высоту Угол наклона грани Радиус вписанной сферы Телесный угол при вершине Правильный тетраэдр
Прямоугольный тетраэдр Тетраэдр, у которого в одной вершине сходятся три прямых угла называют прямоугольным. Такой тетраэдр можно получить, разрезав куб.
Тетраэдры в живой природе Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в строительстве Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Тетраэдр в оптике Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Тетраэдры в микромире Молекула метана СН 4 Молекула аммиака NH 3 Алмаз C тетраэдр с ребром равным 2,5220 ангстрем Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+ Силикаты, в основе структур которых лежит кремнекислородный тетраэдр 4-
Тетраэдры в производстве Форму тетраэдра нельзя назвать удобной, но и у нее есть применение, например, при изготовлении пакетов для молока. Оказалось, что на конвейере удобно склеивать подобные тетраэдры, отрезая заготовки для них от картонного шланга.
Г10(I)-4. Тетраэдр и параллелепипед
Геометрия 10 класс. Глава I. Тест 4.
Вариант 1.
1. Выбрать верные утверждения.
1) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.
2) Параллелепипед ABCDA1B1C1D1 — поверхность, составленная из двух равных прямоугольников ABCD и A1B1C1D1 и четырёх прямоугольников AA1D1D, DD1C1С, BB1C1C и AA1B1B.
3) Диагональю параллелепипеда называется отрезок, соединяющий две вершины любой грани.
4) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.
5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.
2. Назвать все пары скрещивающихся рёбер тетраэдра MPEK на рисунке 1.
A) MP и KE; MK и PE; ME и PK; B) MP и PE; MK и PE; ME и PK;
C) MP и KE; MK и KE; ME и PK; D) MP и KE; MK и PE; ME и EK.
3. Выбрать верные утверждения, используя рисунок 2.
1) Х – точка пересечения прямой МЕ и плоскости АВС.
2) Р – точка пересечения прямой ЕК и плоскости АВD.
3) Точки Х и Р лежат в одной плоскости.
A) 2 и 3; B) 1 и 3; C) 1 и 2; D) 1; 2 и 3.
4. На рисунке 3 точка М принадлежит боковой грани CC1D1D прямоугольного параллелепипеда ABCDA1B1C1D1. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АВС. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA1=9 см.
A) 45 см2; B) 35 см2; C) 63 см2; D) 21 см2.
5. Основанием параллелепипеда ABCDA1B1C1D1 на рисунке 4 является квадрат со стороной 10 см и боковым ребром, равным 12 см. Угол B1BD – прямой. Проведите сечение параллелепипеда через точки B, D и В1 и найдите площадь этого сечения.
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки B1, D1 и М. Какая фигура получилась в сечении?
A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.
Вариант 2.
1. Выбрать верные утверждения.
1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.
2) Два ребра тетраэдра, не имеющие общих вершин, называют смежными.
3) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.
4) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.
5) Две грани параллелепипеда, имеющие общие рёбра, называются противоположными.
A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.
2. Назвать все пары скрещивающихся рёбер тетраэдра KABM на рисунке 1.
A) AK и AB; BK и AM; MK и AB; B) AK и BM; BK и AB; MK и AB;
C) AK и BM; BK и AM; MK и AB; D) AK и BM; BK и AM; MK и MB.
3. Выбрать верные утверждения, используя рисунок 2.
1) Р – точка пересечения прямой АВ и плоскости NMQ.
2) E – точка пересечения прямой AC и плоскости MFQ.
3) Точки E и Р лежат в различных плоскостях.
A) 1; 2 и 3; B) 1 и 3; C) 1 и 2; D) 2 и 3.
4. На рисунке 3 точка М принадлежит боковой грани CC1D1D прямоугольного параллелепипеда ABCDA1B1C1D1. Через точку М проведите сечение параллелепипеда плоскостью, параллельной плоскости АА1D1. Найдите площадь этого сечения, если АВ=5 см, AD=7 см, AA1=9 см.
A) 45 см2; B) 35 см2; C) 63 см2; D) 21 см2.
5. Основанием параллелепипеда ABCDA1B1C1D1 на рисунке 4 является квадрат со стороной 8 см и боковым ребром, равным 7 см. Угол B1BD – прямой. Проведите сечение параллелепипеда через точки B, D и D1 и найдите площадь этого сечения.
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении?
A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.
Вариант 3.
1. Выбрать верные утверждения.
1) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.
2) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.
3) Противоположные грани параллелепипеда параллельны и равны.
4) Секущей плоскостью тетраэдра называют любую плоскость, по одну сторону от которой имеются точки данного тетраэдра.
5) Секущая плоскость пересекает грани параллелепипеда по отрезкам-рёбрам параллелепипеда. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.
A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.
2. Выбрать верные утверждения, используя рисунок 1.
1) M – точка пересечения прямой АP и плоскости A1B1C1.
2) K – точка пересечения прямой PF и плоскости ABD.
3) Точки M и K лежат в одной плоскости.
A) 1; 2 и 3; B) 1 и 3; C) 2 и 3; D) 1 и 2.
3. В тетраэдре DABC на рисунке 2 угол ADB равен 60°, углы АСВ и CBD прямые, AD=BD, АВ=26, DC=31. Найти АС. В ответе записать квадрат получившегося значения.
A) 391; B) 625; C) 380; D) 576.
4. Основанием параллелепипеда ABCDA1B1C1D1 на рисунке 3 является квадрат со стороной 4 см и боковым ребром, равным 6 см. Угол B1BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B1D и найдите площадь этого сечения.
5. В тетраэдре МАВС на рисунке 4 проведено сечение КЕР параллельно грани ВСМ. Площадь треугольника ВСМ равна 60 см2. Найти площадь треугольника КЕР, если АК:КВ=7:3.
A) 29,4 см2; B) 58,8 см2; C) 294 см2; D) 30,4 см2.
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и Т. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.
Вариант 4.
1. Выбрать верные утверждения.
1) Две грани параллелепипеда, имеющие общее ребро, называются смежными.
2) Все рёбра параллелепипеда называются боковыми рёбрами.
3) Секущая плоскость пересекает грани тетраэдра по отрезкам прямых, содержащих рёбра тетраэдра. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.
4) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.
5) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
A) 1; 3; 4; B) 1; 2; 3; C) 1; 3; 5; D) 1; 4; 5.
2. Выбрать верные утверждения, используя рисунок 1.
1) Р – точка пересечения прямой NK и плоскости ACD.
2) E – точка пересечения прямой DK и плоскости A1B1C1.
3) Точки E и Р лежат в различных плоскостях.
A) 2 и 3; B) 1 и 3; C) 1; 2 и 3; D) 1 и 2.
3. В тетраэдре DABC на рисунке 2 углы АСВ, АDВ и CBD — прямые, AD=BD=8, DC=11. Найти АС. В ответе записать квадрат получившегося значения.
A) 72; B) 71; C) 57; D) 64.
4. Основанием параллелепипеда ABCDA1B1C1D1 на рисунке 3 является квадрат со стороной 6 см и боковым ребром, равным 8 см. Угол B1BD – прямой. Проведите сечение параллелепипеда через прямую АС параллельно B1D и найдите площадь этого сечения.
5. В тетраэдре DАВС на рисунке 4 проведено сечение MPK параллельно грани АDС. Площадь треугольника МРК равна 4 см2. Найти площадь треугольника АDС, если СК:ВК=3:5.
A) 10,24 см2; B) 20,48 см2; C) 6,4 см2; D) 8,64 см2.
6. Перечертите рисунок 5 в тетрадь и проведите сечение параллелепипеда через точки М, Р и К. Какая фигура получилась в сечении? A) треугольник; B) четырёхугольник; C) пятиугольник; D) шестиугольник.
Справочные материалы.
1) Поверхность, составленная из четырёх треугольников, называется тетраэдром.
2) Грани тетраэдра – это треугольники, из которых состоит тетраэдр.
3) Тетраэдр имеет 4 грани, 6 рёбер и 4 вершины.
4) Два ребра тетраэдра, не имеющие общих вершин, называют противоположными.
5) Параллелепипед ABCDA1B1C1D1 — поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырёх параллелограммов AA1D1D, DD1C1С, BB1C1C и AA1B1B.
6) Грани параллелепипеда – это параллелограммы, из которых составлен параллелепипед.
7) Параллелепипед имеет 6 граней, 12 рёбер и 8 вершин.
 Две грани параллелепипеда, имеющие общее ребро, называются смежными.
Две грани параллелепипеда, имеющие общее ребро, называются смежными.
9) Две грани параллелепипеда, не имеющие общих рёбер, называются противоположными.
10) Диагональю параллелепипеда называется отрезок, соединяющий две вершины, не принадлежащие одной грани.
11) Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами.
12) Противоположные грани параллелепипеда параллельны и равны.
13) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
14) Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.
15) Секущей плоскостью параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного параллелепипеда.
16) Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.
17) Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.
18) Сечением тетраэдра могут быть только треугольники и четырёхугольники, так как тетраэдр имеет 4 грани.
19) Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники, так как параллелепипеда имеет 6 граней.
Метки: геометрия 10 класс тесты, многогранники, прямые и плоскости, стереометрия