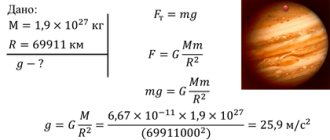
The concept of a vector in space presentation for a geometry lesson (grade 11) on the topic
Slide 1
The concept of a vector in space Author: Kuchaeva Gulnara Azatovna, mathematics teacher of Municipal Educational Institution "Secondary School No. 73" in Orenburg
Slide 2
Concept of a vector A vector is a segment for which it is indicated which of its ends is considered the beginning and which is the end. A B AB a Any point in space is also considered a vector. Such a vector is called zero. MM = 0 M
Slide 3
Concept of a vector The length of a non-zero vector is understood as the length of the segment AB. Designation: | | , | a | The length of the zero vector is considered equal to zero | 0 | =0 AB AB
Slide 4
Collinearity of vectors Non-zero vectors are called collinear if they lie on the same line or on parallel lines. Collinear vectors co-directed and oppositely directed
Slide 5
Co-directionality of vectors Co-directional vectors are vectors lying on one side of the straight line passing through their origins. a b The zero vector is considered codirectional with any vector a ↑↑ b
Slide 6
Opposite direction of vectors Oppositely directed vectors are vectors lying on opposite sides of the straight line passing through their origins. a ba ↑↓ b
Slide 7
Equality of vectors Vectors are called equal if they are codirectional and their lengths are equal. From any point you can plot a vector equal to the given a b c M N
Slide 8
Opposite vectors Vectors are called opposite if they are opposite in direction and their lengths are equal. a b
Slide 9
Check yourself! Is the statement true? Are any two oppositely directed vectors collinear? Are any two collinear vectors co-directional? Are any two equal vectors collinear? Are any two codirectional vectors equal? If , then ? ANSWERS
Slide 10
ANSWERS yes; no, they can be oppositely directed; Yes; no, vectors can have different lengths; Yes.
Slide 11
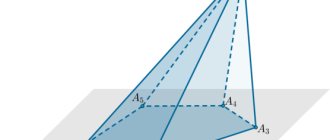
Solving problems No. 320 (a), p. 86 Given: DABC – tetrahedron; AM=MC, BN=NC, CK=KD; A B =3 cm, BC=4 cm, BD=5 cm. Find: , , , , , . Solution. = AB ⟹ =3 cm; =BC ⟹ =4 cm; =BD ⟹ =5 cm. Consider ∆ ABC. = N.M. N – middle of BC, M – middle of AC (by condition) ⟹ NM – middle line ∆ ABC ⟹ NM = AB; NM=1.5 cm ⟹ =1.5 cm . Similarly: =2.5 cm. Because N is the middle of BC ⟹ BN= BC, BN= 2 cm. =BN ⟹ = 2 cm. Answer: 3 cm; 4 cm; 5 cm; 1.5 cm; 2 cm; 2.5 cm. DABCMNK
Slide 12
Solution of problems No. 322 (a, c) According to the property of a parallelepiped: a) ; V) . ADBCA 1 D 1 B 1 C 1 M K
Slide 13
Homework § 1 (p. 84-85), No. 320 (b), 321 (a), 322 (b), 326 (a, b).
Slide 14
sources Geometry. Grades 10-11: textbook. for general education institutions: basic and profile. levels / [L. S. ATANASYAN, V. F. Butuzov, S. B. Kadomtsev, etc.]
Vector coordinates
Let's remember how we found the coordinates of a vector on a plane.
Taking advantage of the fact that any vector can be expanded into two non-collinear vectors, we specified unit vectors on the axes. Thus, any vector can be expanded into given unit vectors, and the coordinates of the vector are the coefficients of this expansion.
You also already know that any vector in space can be expressed in terms of 3 non-coplanar vectors, that is, vectors that do not lie in the same plane.
Let us depict the rectangular coordinate system Oxyz. On each of the positive axes, we plot unit vectors from the origin.
Letter i
Let us denote the unit vector of the Ox axis, the letter
j
- the unit vector of the Oy axis, and the letter
k
- the unit vector of the Oz axis.
Definition:
Vectors i
,
j
,
k
will be called
coordinate vectors
.
It is clear that they are non-coplanar
.
And therefore any vector of space can be decomposed into unit vectors i
,
j
,
k
. Moreover, the expansion coefficients x, y and z are determined in a unique way.
The coefficients x, y and z are called coordinates
vector
p
in a given coordinate system. We will write the coordinates of the vector in curly brackets in the sequence x, y, z.
Exercise:
Using the expansions of vectors into coordinate vectors, write down their coordinates.
Solution:
Exercise:
Using the coordinates of the vectors, we write their expansions in coordinate vectors
i
,
j
,
k
.
Solution:
Task:
In a rectangular parallelepiped