Понятие вектора в пространстве презентация к уроку по геометрии (11 класс) по теме
Слайд 1
Понятие вектора в пространстве Автор: Кучаева Гульнара Азатовна , учитель математики МОБУ «СОШ № 73» г. Оренбурга
Слайд 2
Понятие вектора Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом. А В АВ a Любая точка пространства также рассматривается как вектор. Такой вектор называют нулевым. ММ = 0 М
Слайд 3
Понятие вектора Под длиной ненулевого вектора понимают длину отрезка АВ. Обозначение: | | , | a | Длина нулевого вектора считается равной нулю | 0 | =0 АВ АВ
Слайд 4
Коллинеарность векторов Ненулевые вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых. Коллинеарные вектора сонаправленные п ротивоположно направленные
Слайд 5
Сонаправленность векторов Сонаправленные векторы – векторы, лежащие по одну сторону от прямой, проходящей через их начала. а b Нулевой вектор считается сонаправленным с любым вектором a ↑↑ b
Слайд 6
Противоположная направленность векторов Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала. а b a ↑↓ b
Слайд 7
Равенство векторов Вектора называются равными , если они сонаправлены и их длины равны. От любой точки можно отложить вектор, равный данному а b с М N
Слайд 8
Противоположность векторов Вектора называются противоположными , если они противоположно направленны и их длины равны. а b
Слайд 9
Проверь себя! Справедливо ли утверждение? Любые два противоположно направленных вектора коллинеарны ? Любые два коллинеарных вектора сонаправлены ? Любые два равных вектора коллинеарны ? Любые два сонаправленных вектора равны? Если , , то ? ОТВЕТЫ
Слайд 10
ОТВЕТЫ да; нет, могут быть противоположно направленными; д а; нет, вектора могут иметь разную длину; д а.
Слайд 11
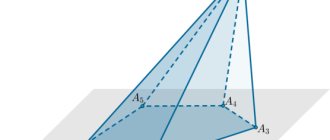
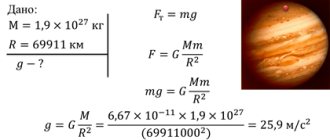
Решение задач № 320 (а), с. 86 Дано: DABC – тетраэдр; AM=MC , BN=NC , CK=KD; A В =3 см, BC=4 см, BD=5 см. Найти: , , , , , . Решение. = AB ⟹ =3 см ; =BC ⟹ =4 см ; =BD ⟹ =5 см. Рассмотрим ∆ ABC . = NM . N – середина BC , М – середина АС (по условию) ⟹ NM — средняя линия ∆ ABC ⟹ NM = AB; NM=1,5 см ⟹ =1,5 см . Аналогично: =2,5 см. Т. к. N – середина BC ⟹ BN= BC, BN= 2 см. =BN ⟹ = 2 см. Ответ: 3 см; 4 см; 5 см; 1,5 см; 2 см; 2,5 см. D A B C M N K
Слайд 12
Решение задач № 322 (а, в) По свойству параллелепипеда: а) ; в) . A D B C A 1 D 1 B 1 C 1 M К
Слайд 13
Домашнее задание § 1 (с. 84-85), № 320 (б), 321 (а), 322 (б), 326 (а, б).
Слайд 14
источники Геометрия. 10—11 классы : учеб. для общеобразоват . учреждений : базовый и профил . уровни / [ Л. С. АТАНАСЯН , В. Ф. Бутузов, С. Б. Кадомцев и др.]
Координаты вектора
Вспомним, как мы находили координаты вектора на плоскости.
Пользуясь тем, что любой вектор можно разложить по двум неколлинеарным векторам, на осях мы задавали единичные векторы. Таким образом, любой вектор можно разложить по данным единичным векторам, а координатами вектора являются коэффициенты этого разложения.
Так же вам уже известно, что любой вектор пространства можно выразить через 3 некомпланарных вектора, то есть векторы, не лежащие в одной плоскости.
Изобразим прямоугольную систему координат Охуz. На каждой из положительных осей от начала координат отложим единичные векторы.
Буквой i
обозначим единичный вектор оси Оx, буквой
j
— единичный вектор оси Оy, буквой
k
— единичный вектор оси Оz.
Определение:
Векторы i
,
j
,
k
будем называть
координатными векторами
.
Понятно, что они являются некомпланарными
. И поэтому любой вектор пространства можно разложить по единичным векторам
i
,
j
,
k
. Причём коэффициенты разложения х, у и z определяются единственным образом.
Коэффициенты х, у и z называют координатами
вектора
р
в данной системе координат. Координаты вектора будем записывать в фигурных скобках в последовательности х, у, z.
Задание:
Пользуясь разложениями векторов по координатным векторам, записать их координаты.
Решение:
Задание:
пользуясь координатами векторов, запишем их разложения по координатным векторам
i
,
j
,
k
.
Решение:
Задача:
В прямоугольном параллелепипеде