Development of the lesson “Problems on the coordinate plane”
Topic: Problems on the coordinate plane.
Target:
- Application of algebraic apparatus to solving problems with geometric themes;
- Remember the geometric meaning of the coefficients k and l in the linear equation y = kx + l;
- How to apply the condition of parallel lines;
- Recall the algebraic expression of the fact “a point with given coordinates belongs (or does not belong) to the graph of the equation”;
- How to find the coordinates of the point of intersection of lines by composing and solving the corresponding system.
Students must:
— know the geometric meaning of the coefficients k and l in the linear equation y = kx + l;
- know and be able to apply the condition of parallelism of lines;
— know the algebraic expression of the fact “a point with given coordinates belongs (or does not belong) to the graph of the equation”;
- be able to freely solve systems of linear equations (problems of a technical nature should not push the ideological side of the issue into the background);
- be able to find the coordinates of the point of intersection of lines by compiling and
solving the appropriate system.
During the classes.
- Organizational moment.
- AOZ.
- Learning new things.
Using systems of equations, you can determine the relative positions of lines on the coordinate plane and find the coordinates of their intersection points. Thus, algebra can work on geometry.
Using equations, you can solve other problems related to straight lines on the coordinate plane.
- -So, how to determine the relative position of two straight lines on a plane? ( compare slopes
)
— How to find the intersection points of graphs? (create a system of equations and solve it)
— How to determine the point of intersection of the graph with the coordinate axes using its equation? ( l
– shows the point of intersection with the Oy axis; to find the point of intersection with the Ox axis, it is necessary to y = 0 and find the corresponding value of the argument).
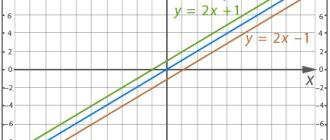
- y=-2x +
l is given .
-Name some equation of a line that is parallel to this line and passes through a point
- A(0; 4)
Since the lines must be parallel, then k=-2. The point itself is the point of intersection with the Oy axis, which means l
= 4
y = -2x + 4
- B (5; 0)
Since the lines must be parallel, then k=-2. Let's find the value of l ,
by substituting the coordinates of the point into the appropriate equation.
0 = -2 · 5 + l
l
= 10
y = -2x +10
- C(-1;2)
- Let us write down the equation of the line passing through the points A(-
1; 2) and B(3; 4).
-Name the general form of the equation of a straight line.
y=
k x + l
- What needs to be found to draw up the equation of a straight line?
k
and l
-How many equations do we need to create?
Answer: y=0.5x + 2.5.
- Formation of skills and abilities.
№685 b
Use problem 1 from the textbook as an example.
y = - 0.5x + 2.
№686
№687 (b)
First you need to write the equation of the line in the form y = kx + b. Then
Let's come to an exercise like 685 b). As a sample you can
use task 1 from the theoretical part of the text.
- Lesson summary.
- Reflection.
“Imagine your life as a coordinate plane.
The Y axis is your position in society.
The X axis is moving forward, towards the goal, towards your dream.
And as we know, it is endless... We can fall down, going further and further into minus, we can remain at zero and do nothing, absolutely nothing. We can rise up, we can fall, we can go forward or go back, and all because our whole life is a coordinate plane and the most important thing here is what your coordinate is...”
- Homework. No. 684a, No. 685a, No. 687a.
Summary of a lesson in mathematics on the topic “Coordinate plane”
Lesson objectives:
Students:
- generalization and consolidation of material on the topic: “ Coordinate plane ”;
— repetition of basic concepts and definitions of the topic;
— testing and improving the skills of constructing points at given coordinates and the skills of determining the coordinates of points;
Educational:
— development of skills in working with test tasks;
— development of the ability to correctly and competently express one’s thoughts;
— development of mathematical thinking;
Educational:
— increasing learning motivation through the use of ICT;
— instilling interest in mathematics by including gaming technologies in the lesson
Lesson objectives:
consolidate the concepts of: coordinate system, coordinate axes (abscissa axis, ordinate axis), coordinate plane, abscissa and ordinate of a point;
to consolidate in students the skills and abilities to determine the coordinates of a point given in the coordinate plane, and to mark a point with given coordinates in the coordinate plane ;
be able to obtain the necessary information using available sources (reference books, textbooks)
improve group work skills, learn to express and defend your opinion;
instill skills of independent creative work;
instill skills of self-control and mutual control;
Lesson type: Combined lesson.
Required equipment and materials:
Multimedia office, interactive whiteboard, handouts (applications),
presentation, evaluation sheet for entering intermediate grades to calculate the final grade. Textbook of mathematics - A. G. Mordkovich, Mathematics 6th grade.
During the classes:
- Organizational moment (4 groups of students)
(Defining the topic of the lesson) Slide2.
— What concept are the phrases indicated on the slide related to?
Students independently determine the topic of the lesson “Coordinate plane” Slide 2.
- Updating basic knowledge. Checking d/z
- Where in practical life do we encounter the use of coordinates? Slide4
Students' answers: determine the place in the theater, the position of the piece on the chessboard, on the field of the game "Sea Battle", a geographical map, etc.
– Today in class we will continue to study this topic. We open the notebooks, write down the date and topic of the lesson.
– What goals will we set for ourselves for this lesson? Formulate and justify your goals. (Children formulate the goals of the lesson.)
– By working in groups and performing various tasks, you will show us your knowledge, skills and abilities, and the ability to apply them in various situations.
2) Work in groups in pairs. (Annex 1)
3) At this time, prepare homework No. 422 (g) on the interactive whiteboard in the “Living Mathematics” program
Checking the homework and asking questions from each group to the person answering at the board on this topic.
3. Formation of skills and abilities. The main part of the lesson “The game is a journey”
— 1 stop “HISTORICAL” Slide 5 — 6
Points are indicated on the coordinate plane; using the coordinates you need to compose a word.
After the definition of the word - DESCARTES, the student gives a speech with historical information about DESCARTES (independent work of the student) Slide.
— 2nd stop “GEOMETRICAL” Slide 7
Appendix 2 (Calculate the perimeter and area of the figure) Each group receives its own task. (followed by verification) Slide 8
— 3rd stop “MOST ATTENTIVE” On the board, representatives from each of the four groups alternately perform tasks for a while. Slide 9 – 12
3. - 4th stop “FISMINUTKA”
- Workshop
- 5th stop. “MATHEMATICAL” (groups take turns doing tasks on the board) Slide 13
— 6 stop “ARTISTS”
We continue our journey. Let's determine the coordinates of the last stop. (5; - 3).
This is a picturesque place where you just want to “take up a brush” and capture what you see.
Each group receives tasks with coordinates. We mark the points, immediately connecting them. The result should be a picture.
Children work to music.
See document
VI. Summarizing. (final stage with control sheets)
Homework: Construct your figure on the coordinate plane and write down the coordinates of the points along which this figure is constructed.
IX. Reflection of activity.
You did a really good job in class today, well done!
Evaluate your knowledge acquired in the lesson. Match your mood with the smiley face. (Application).
Lesson summary “Coordinate plane”, 7th grade. Algebra
Lesson topic: “Coordinate plane.”
Lesson objectives:
- continue studying the coordinate system; lead to the possibility of specifying the position of a point on the coordinate plane using a pair of numbers, using the analogy of entering coordinates in geography, the coordinates of pieces on a chessboard; analysis of the position of a point on the coordinate plane; demonstrate the possibility of connecting geometric figures with the coordinate plane;
- develop cognitive activity and creative abilities;
- to cultivate interest in the subject, awareness of one’s actions and their application in real life.
Equipment:
computer, screen, educational - demonstration program “Coordinate plane”
Lesson plan.
I. Organizational moment.
(students sit down at the computers; before the start of the lesson, divide the children into four groups if desired to work in groups.)
1 slide.
—
Do you like to solve riddles? Guess what it's about using the clues.
1. Children's reasoning: this is a canvas on which you can see everything at once.
2. It can be sanatorium-resort, astronomical, or gaming.
3. The oldest is made on a clay tablet, it dates back to 3800 BC. it depicts r. Euphrates, flowing through Northern Mesopotamia, Iraq;
4. In Ozhegov’s dictionary its first meaning is: drawing of the surface of the Earth, a celestial body or the starry sky.
(map)
Do you know that
The Guinness Book of Records includes the largest relief map of California, weighing 39 tons, made by Reuben Hall in 1924. Currently stored at Hamilton Air Force Base, Novato, California, it measures 137 by 5 m.
-We got a little distracted, and so, the topic of today’s lesson... please read it on the slide of the computer presentation. (coordinate plane)
-Why do you think we remembered the geographical map at the beginning of the lesson? How to determine the location of a city on a map?
How many difficulties did the heroes of Jules Verne’s novel “The Children of Captain Grant” have to endure, and it all happened because of a note:
“On June 7, 1862, the three-masted ship Britannia Glasgow was wrecked ... drive ... south ... coast ... two sailors ... pl. Captain Gr... reach...contin... pl. ...cruel...ind...thrown this document...longitude and latitude 37°11...help them...they will die.”
It proved impossible to reconstruct the longitude.
To determine the location of an island, village, mountain and put them on a map, how many numbers are required?
2 slide.
— Determine the coordinates of Stavropol. (So, the parallel of 45° N and the meridian of 42° E intersect in the city of Stavropol. In the southwestern region of the regional center there is a street called “Forty-fifth Parallel.”)
It turns out that geographic coordinates were introduced 200 years BC by the Greek scientist Hipparchus.
In the 14th century, the French mathematician Orsem introduced, by analogy with geographical coordinates, coordinates on a plane. He proposed covering the plane with a rectangular grid and called latitude and longitude what we now call abscissa and ordinate.
On its basis, the coordinate method arose, connecting geometry with algebra. The main credit for the creation of this method belongs to the great French mathematician, and you will find out his last name after the warm-up
II . Updating knowledge.
-Now let’s do a little warm-up in geography and mathematics. I read the question, you answer it “to yourself”, writing the first letter on a piece of paper.
1. The largest continent. (Eurasia) E.
2. A polynomial consisting of two monomials is called. (binomial) D
3. Serial number of the longest quarter. (Three) T
4. The name of the country in which we live. (Russia) R
5. The last letter in the name of a polygon with the smallest number of sides. (Triangle) K
6. The horizontal coordinate axis is called the x-axis, or axis... (Abscissus) A
Solve the anagram, use the letters to make up the name of the great mathematician (Descartes) 3 slide
So, today in the lesson we will repeat what
coordinate lines the coordinate system is formed , which lines are called coordinate axes , their names (write the concepts on the board).
Let's learn how to determine the coordinate of a point on a plane and construct it.
slide 4
— What does the expression “A rectangular coordinate system is specified on the plane” mean? (two mutually perpendicular coordinate lines, with the indicated intersection point - the origin)
— How are straight lines located on a plane?
- What are they called, what direction do they have?
— What do the arrows show? Is it possible to change their direction?
III . Working on a new topic.
In geometry, we became acquainted with the undefined concepts of plane, straight line and point. If you draw two mutually perpendicular lines on a plane, how many parts will they divide the plane into? (4)
Right angles formed by coordinate axes are called coordinate angles.
The next slide shows their numbering.
5 slide.
6 slide.
What is shown in the figure? (point in coordinate area)
A pair of numbers (4;3) is called the coordinates of point A on the coordinate plane
.
, the first of these numbers is called the abscissa of point A,
the second number is called
the ordinate of point A.
Think about why the number 4 is the abscissa of point A, and the number 3 is its ordinate (4 is the distance to the abscissa, 3 is the distance to the ordinate)
How to find the coordinates of point A given in a rectangular coordinate system?
1. Draw a line parallel to the y-axis through point A and find the coordinate of the point of intersection of this line with the x-axis - this will be the abscissa of point A.
2. Draw a line parallel to the x-axis through point A and find the coordinate of the point of intersection of this line with the y-axis - this will be the ordinate of point A.
x=4 equation of a straight line parallel to the y-axis, y=3 ur pr. par. X.
slide 7.
Determine and record the coordinates of the points on the slide. Test yourself by clicking your mouse.
What coordinate angle do the points belong to?
If a point belongs to 1 coor angle, then x is....
We looked at how to find the coordinates of a point, but how to construct a point from its coordinates?
Slide 8.
IV .
Physical exercise. (invite groups to sit at tables)
1) pulling the earlobes from top to bottom; 2) pulling the auricle upward; 3) pulling the auricle outward; 4) circular movements of the auricle clockwise and counterclockwise.
5) close your eyes and imagine the colors of the rainbow one by one as clearly as possible;
Mathematical illusions.
Is the cylinder positioned from left to right or right to left?
How many cubes are there, 6 or 7?
V. Group work.
Mark points in this coordinate plane. Place the finished images on the board using a magnet.
Read the legend about the constellations.
V. Work on workbooks,
progress to the topic “Geometric figures on the coordinate plane”
Open workbooks “Geometry” on page 29 No. 66, task 1
.
Additional task. (dictation)
Under dictation, mark the coordinates of the points. (on a computer)
The legend of the chessboard.
The Hindu king, Sheram, met her, he was delighted with her wit and the variety of possible positions.
Having learned that it was invented by one of his subjects, the king ordered to call him to personally reward him for his successful invention.
“I wish to reward you, Seth, for the wonderful game you came up with.”
The sage bowed.
- Name the reward and you will receive it.
“Great is your kindness, lord.” Lord, order me to give one grain of wheat for the first square of the chessboard.
— A simple grain of wheat? – the king was amazed.
- Yes, lord. For the second cell - 2 grains, for the third - 4, for the fourth - 8, for the fifth - 16, for the sixth - 32,...
“That’s enough,” the king interrupted him. – You will receive your grains for all 64 squares of the board. Truly, as a teacher, you could set a better example of respect for the kindness of your sovereign. Go. My servants will bring you a bag of wheat.
Seta smiled and left the hall.
The senior court mathematician asks to listen to the report.
This number is so big...
Tsar, if you absolutely want to deliver what you have promised, then order the earthly kingdoms to be turned into arable fields, order the seas and oceans to be drained, order the ice and snow covering the distant northern deserts to be melted. Let their entire space be completely sown with wheat. And give everything that grows in these fields to Sethe.
- Name this monstrous number.
18 quintillion 446 quadrillion 744 trillion 703 billion 709 million 551 thousand 615
, oh lord!
See what mysteries are hidden in the 64 squares of the chessboard. You will learn a lot of interesting things about the coordinate plane and geometric figures on it as you further study mathematics.
V I. _ Lesson summary.
- Our lesson ends. What was the most important thing about it? (The most important thing was working with the coordinate system, because we learned to determine the position of a point on the coordinate plane, write down the coordinates of the point. Construct a point using given coordinates.)
— What did you like most?
Homework: paragraph 27 No. 772, 773; prepare a message about Rene Descartes, draw a picture, specifying the coordinates of the points.
6