Consideration of cases of parallel and coinciding lines
Let's look at an example:
Example 1:
, ,
Let's build graphs of these functions. Each of them. The first, the second, the third. Recall that the parameters k and m are determined from the standard form of a linear equation, the parameter is the ordinate of the point of intersection of the line with the y-axis. In addition, note that the coefficient is responsible for the angle of inclination of the straight line to the positive direction of the x-axis; in addition, if it is positive, then the function will increase, and if negative, it will decrease. The coefficient is called the slope.
Let's create tables for plotting:
| X | 0 | -0,5 |
| at | 1 | 0 |
Table for the first function;
| X | 0 | 1 |
| at | 0 | 2 |
Table for the second function;
| X | 0 | 0,5 |
| at | -1 | 0 |
Table for the third function;
Obviously, all constructed lines are parallel, because their angular coefficients are the same. The functions differ only in the value of m.
Rice. 1.
Let's draw a conclusion. Let two arbitrary linear functions be given:
And
If but then the given lines are parallel.
If and then the given lines coincide.
The study of the relative position of graphs of linear functions and the properties of their parameters is the basis for the study of systems of linear equations. We must remember that if the lines are parallel, then the system will have no solutions, and if the lines coincide, then the system will have an infinite number of solutions.
Algebra. Lesson 5. Graphs of Functions
Watch free video lessons on the Hedgehog Clear channel on the topic “Graphs of functions”.
Video lessons on the Hedgehog channel Clearly. Subscribe!
Page content:
- Cartesian coordinate system
- Function
Direct Parabola Hyperbola Square Root
- Increasing/decreasing function
- Largest/smallest function value
- Examples of solutions to tasks from the OGE
A coordinate system is two mutually perpendicular coordinate lines intersecting at a point, which is the origin for each of them.
Coordinate axes are straight lines that form a coordinate system.
The abscissa axis (x axis) is the horizontal axis.
The ordinate axis (y axis) is the vertical axis.
A function is a mapping of elements of set X to set Y. In this case, each element x of the set X corresponds to one single value y of the set Y.
A linear function is a function of the form y = ax + b where a and b are any numbers.
The graph of a linear function is a straight line.
Let's look at what the graph will look like depending on the coefficients a and b:
If a > 0, the straight line will pass through the I and III coordinate quarters.
b is the point of intersection of the line with the y axis.
If a < 0, the straight line will pass through the II and IV coordinate quarters.
b is the point of intersection of the line with the y axis.
If a = 0, the function becomes y = b.
Let us separately highlight the graph of the equation x = a.
Important : this equation is not a function since the definition of a function is violated (the function associates each element x of the set X with one single value y of the set Y). This equation assigns one element x to an infinite set of elements y. However, it is possible to construct a graph of this equation. Let’s just not call it the proud word “Function”.
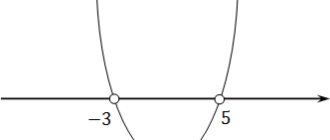
The graph of the function y = ax 2 + bx + c is a parabola .
In order to unambiguously determine how the graph of a parabola is located on a plane, you need to know what the coefficients a, b, c influence:
- The coefficient a indicates where the branches of the parabola are directed.
- If a > 0, the branches of the parabola are directed upward.
- If a < 0, the branches of the parabola are directed downward.
- The coefficient c indicates at what point the parabola intersects the y-axis.
- The coefficient b helps to find x in - the coordinate of the vertex of the parabola.
x in = − b 2 a
- The discriminant allows you to determine how many points of intersection the parabola has with the axis.
- If D > 0 – two points of intersection.
- If D = 0 – one intersection point.
- If D < 0 – there are no intersection points.
The graph of the function y = kx is a hyperbola .
A characteristic feature of a hyperbola is that it has asymptotes.
The asymptotes of a hyperbola are straight lines, to which it tends, going to infinity.
The x-axis is the horizontal asymptote of the hyperbola
The y-axis is the vertical asymptote of the hyperbola.
On the graph, asymptotes are marked with a green dotted line.
If the coefficient k > 0, then the branches of the hyperole pass through the I and III quarters.
If k < 0, the branches of the hyperbola pass through the II and IV quarters.
The smaller the absolute value of the coefficient k (coefficient k without taking into account the sign), the closer the branches of the hyperbola are to the x and y axes.
The function y = x has the following graph:
The function y = f ( x ) increases on the interval if a larger value of the argument (larger value of x ) corresponds to a larger value of the function (larger value of y ).
That is, the more (to the right) the X, the larger (higher) the Y. The graph goes up (look from left to right)
Examples of increasing functions:
The function y = f (x) decreases on the interval if a larger value of the argument (larger value of x) corresponds to a smaller value of the function (larger value of y).
That is, the more (to the right) the X, the smaller (lower) the I. The graph goes down (looking from left to right).
Examples of decreasing functions:
In order to find the largest value of the function , we find the highest point on the graph and look at its coordinate along the ordinate axis (along the y axis). This value will be the largest value of the function.
In order to find the smallest value of the function , we find the lowest point on the graph and look at its coordinate along the ordinate axis (along the y axis). This value will be the smallest value of the function.
Consideration of the case of intersecting lines
Let's consider the case when the angular coefficients are not equal. Let's look at an example:
Example 3 – find graphically the point of intersection of lines:
Both functions have a graph - a straight line.
The angular coefficient of the first function, the second function, , means the lines are not parallel and do not coincide, which means they have an intersection point, and a unique one.
Let's create tables for plotting:
| X | 0 | 1,5 |
| at | -3 | 0 |
Table for the first function;
| X | 0 | 4 |
| at | 2 | 0 |
Table for the second function;
Rice. 6.
It is obvious that the lines intersect at the point (2; 1)
Let's check the result by substituting the obtained coordinates into each function:
Consideration of an example on the properties of function parameters
Let's consider the tasks.
Example 2 – determine the signs of parameters k and m from a given graph of the function:
The straight line intersects the y-axis in its positive ray, which means m has a plus sign, the angle between the straight line and the positive direction of the x-axis is acute, the function increases, which means the k sign is also plus.
Rice. 2.
The straight line intersects the y-axis in its positive ray, which means m has a plus sign, the angle between the straight line and the positive direction of the x-axis is obtuse, the function decreases, which means the k sign is minus.
Rice. 3.
The straight line intersects the y-axis in its negative ray, which means m has a minus sign, the angle between the straight line and the positive direction of the x-axis is acute, the function increases, which means the k sign is plus.
Rice. 4.
The straight line intersects the y-axis in its negative ray, which means m has a minus sign, the angle between the straight line and the positive direction of the x-axis is obtuse, the function decreases, which means the sign of k is also minus.
Rice. 5.
Solving the example, identifying the properties of the parameters of a linear function
Example 2:
Let's plot two linear functions: (4), (5)
In function 4
In function 5
To construct graphs, we will draw up tables in which we will write down the points of their intersection with the coordinate axes:
| X | 0 | -3 |
| at | m=3 | 0 |
Table for function 4;
| X | 0 | 3 |
| at | m=3 | 0 |
Table for function 5;
So, from the construction we see that when (straight line) the angle between the straight line and the positive direction of the x-axis is acute, and when (straight line) the angle between the straight line and the positive direction of the x-axis is obtuse.
The root of the function 4 is the number -3, because it is at this value of x that the function goes to zero.
The root of the function 5 is the number 3, since for a given value of x the function goes to zero.
Note that the solution to the following system:
Is the point (0; 3).