Solving physical problems or examples in mathematics is completely impossible without knowledge of the derivative and methods for calculating it. The derivative is one of the most important concepts in mathematical analysis. We decided to devote today’s article to this fundamental topic. What is a derivative, what is its physical and geometric meaning, how to calculate the derivative of a function? All these questions can be combined into one: how to understand the derivative?
Daily newsletter with useful information for students of all directions - on our telegram channel.
Geometric and physical meaning of derivative
Let there be a function f(x) defined in some interval (a, b) . Points x and x0 belong to this interval. When x changes, the function itself changes. The change in the argument is the difference between its values x-x0 . This difference is written as delta x and is called the increment of the argument. A change or increment of a function is the difference between the values of a function at two points. Definition of derivative:
The derivative of a function at a point is the limit of the ratio of the increment of the function at a given point to the increment of the argument when the latter tends to zero.
Otherwise it can be written like this:
What's the point of finding such a limit? And here's what it is:
Geometric meaning of the derivative: the derivative of a function at a point is equal to the tangent of the angle between the OX axis and the tangent to the graph of the function at a given point.
The physical meaning of the derivative: the derivative of a path with respect to time is equal to the speed of rectilinear motion.
Indeed, since school days, everyone knows that speed is the quotient of the path x=f(t) and time t . Average speed over a certain period of time:
To find out the speed of movement at time t0, you need to calculate the limit:
By the way, read about what limits are and how to solve them in our separate article.
Let us give an example illustrating the practical application of the derivative. Let the body move according to the law:
We need to find the speed at time t=2c. Let's calculate the derivative:
Test "Geometric meaning of derivatives."
Option #1
1
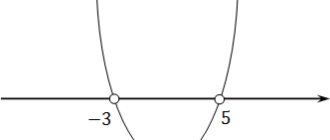
The figure shows a graph of the derivative of the function f(x), defined on the interval (−10; 8). Find the number of maximum points of the function f(x) on the interval [−9;6].
2.
The figure shows a graph of the derivative y = f'(x) of the function y = f(x), defined on the interval (−4; 8). At what point of the segment [−3; 1] does the function y = f(x) take the smallest value?
3.
The figure shows a graph of the derivative of the function and eight points on the x-axis: ,. At how many of these points does the function decrease?
4.
The figure shows a graph of y=f'(x) - the derivative of the function f(x), defined on the interval (−8; 3). Find the intervals of increase of the function f(x). In your answer, indicate the sum of integer points included in these intervals.
Option No. 2
1.
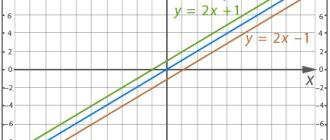
The figure shows a graph of the derivative of a function. Find the abscissa of the point at which the tangent to the graph is parallel to or coincides with the x-axis.
2.
The figure shows a graph of the derivative of a function defined on the interval (−8; 9). Find the number of minimum points of the function belonging to the segment [−4; 8].
3.
The figure shows a graph of the derivative of the function y=f(x), defined on the interval (−7; 4). Find the intervals of decrease of the function.
In your answer, indicate the sum of integer points included in these intervals.
4.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−11; 11). Find the number of extremum points of the function f(x) on the interval [−10; 10].
Test "Geometric meaning of derivatives."
Option No. 3
1.
The figure shows a graph of the function y = f(x), defined on the interval (−2; 12). Find the sum of the extremum points of the function f(x).
2.
The figure shows a graph of the derivative of the function f(x). Find the abscissa of the point at which the tangent to the graph y = f(x) is parallel to or coincides with the line y = 6x.
3.
The figure shows a graph of the derivative of a function defined on the interval. Find the number of extremum points of the function on the segment
4.
The function y = f (x) is defined and continuous on the interval [−5; 5]. The figure shows a graph of its derivative. Find the point x0 at which the function takes on its smallest value if f (−5) ≥ f (5).
Test "Geometric meaning of derivatives."
Option number 4.
The figure shows a graph of the derivative of a function defined on the interval. At what point on the segment does it have the smallest value?
The figure shows a graph of the derivative of the function. Six points are marked on the abscissa axis: , , , , . How many of these points lie on intervals of increasing function
The figure shows a graph of the derivative of a function. Find the abscissa of the point at which the tangent to the graph is parallel to or coincides with the line.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−7; 4). At what point of the segment [−6; −1] does the function f(x) take the greatest value?
Option number 5.
1.
The figure shows a graph of the function y=f(x), defined on the interval (−5; 5). Find the number of points at which the tangent to the graph of the function is parallel to or coincides with the straight line y = 6.
2.
The figure shows the graph of the function and the tangent to it at the abscissa point. Find the value of the derivative of the function at the point
3.
The figure shows a graph of the function and eight points on the x-axis: , , , , . At how many of these points is the derivative of the function positive?
4.
The figure shows a graph of the function f(x) defined on the interval (−5; 5). Find the number of points at which the derivative of the function f(x) is equal to 0.
Option number 6.
1.
The figure shows a graph of the function y=f(x), defined on the interval (−1; 12). Determine the number of integer points at which the derivative of the function is negative.
2.
The figure shows the graph of the function
, defined on the interval (-3;11) . Find the number of points at which the tangent to the graph of the function is parallel to the straight line y = - 11
3.
The figure shows the graph of the function y = f(x) and the tangent to it at the point with the abscissa x0. Find the value of the derivative of the function f(x) at the point x0.
4.
.
The figure shows a graph of the function y=f(x), defined on the interval (−3; 9). Find the number of points at which the tangent to the graph of the function is parallel to or coincides with the straight line y = 12.
Option number 7.
1.
The figure shows a graph of the function defined on the interval (−6; 8). Determine the number of integer points at which the derivative of the function is positive.
2.
The figure shows the graph of the function y=f(x) and the tangent to it at the point with the abscissa x0. Find the value of the derivative of the function f(x) at the point
3.
The figure shows a graph of the derivative of a function defined on the interval. Determine the number of integer points at which the derivative of the function is positive
4.
The figure shows a graph of the function y=f(x), defined on the interval (−5; 7). Find the sum of the extremum points of the function f(x).
Option number 8.
1.
The figure shows a graph of the function and twelve points on the x-axis: , , , , . At how many of these points is the derivative of the function negative?
2.
The figure shows the graph of the function y=f(x) and the tangent to it at the point with the abscissa x0. Find the value of the derivative of the function f(x) at the point x0.
3.
The figure shows a graph of the function
y=f(x)
.
The straight line passing through the origin touches the graph of this function at the abscissa point 8. Find f'
(8).
4.
The figure shows a graph of the function y=f(x). The line passing through the origin touches the graph of this function at the abscissa 10. Find f'(10).
Option number 9.
1.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−6; 5). Find the intervals of decrease of the function f(x). In your answer, indicate the sum of integer points included in these intervals.
2.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−7; 14). Find the number of maximum points of the function f(x) on the interval [−6; 9].
3.
The figure shows a graph of the derivative of a function defined on the interval. At what point on the segment does it have the smallest value?
4.
The figure shows a graph of the function y=f(x), defined on the interval (−1; 12). Determine the number of integer points at which the derivative of the function is negative.
5.
The figure shows the graph of the function y=f(x) and the tangent to it at the point with the abscissa x0. Find the value of the derivative of the function f(x) at the point x0.
6.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−9; 3). Find the number of points at which the tangent to the graph of the function f(x) is parallel to or coincides with the straight line y = 2x − 19.
7.
The figure shows a graph of the derivative of the function f(x), defined on the interval (−2; 12). Find the intervals of decrease of the function f(x). In your answer, indicate the length of the largest of them.
8.
The figure shows a graph of a function defined on the interval. Determine the number of integer points at which the derivative of the function is negative.
Rules for finding derivatives
The process of finding the derivative itself is called differentiation. A function that has a derivative at a given point is called differentiable.
How to find the derivative? According to the definition, you need to create a ratio between the increment of a function and an argument, and then calculate the limit as the increment of the argument tends to zero. Of course, you can calculate all derivatives this way, but in practice this is too long a path. Everything has long been calculated before us. Below we present a table with derivatives of elementary functions, and then consider the rules for calculating derivatives, including derivatives of complex functions with detailed examples.
By the way! For our readers there is now a 10% discount on any type of work
Rule one: set a constant
The constant can be taken out of the derivative sign. Moreover, it needs to be done. When solving examples in mathematics, make it a rule - if you can simplify an expression, be sure to simplify .
Example. Let's calculate the derivative:
Rule two: derivative of the sum of functions
The derivative of the sum of two functions is equal to the sum of the derivatives of these functions. The same is true for the derivative of the difference of functions.
We will not give a proof of this theorem, but rather consider a practical example.
Find the derivative of the function:
Solution:
Rule three: derivative of the product of functions
The derivative of the product of two differentiable functions is calculated by the formula:
Example: find the derivative of a function:
Solution:
It is important to talk about calculating derivatives of complex functions here. The derivative of a complex function is equal to the product of the derivative of this function with respect to the intermediate argument and the derivative of the intermediate argument with respect to the independent variable.
In the above example we come across the expression:
In this case, the intermediate argument is 8x to the fifth power. In order to calculate the derivative of such an expression, we first calculate the derivative of the external function with respect to the intermediate argument, and then multiply by the derivative of the intermediate argument itself with respect to the independent variable.