Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
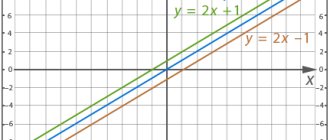
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Тест «Геометрический смысл производной».
Вариант № 1
1
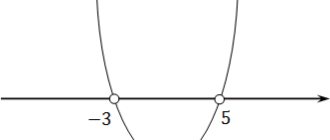
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].
2.
На рисунке изображён график производной y = f'(x) функции y = f(x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция y = f(x) принимает наименьшее значение?
3.
На рисунке изображён график производной функции и восемь точек на оси абсцисс: ,. В скольких из этих точек функция убывает?
4.
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (−8; 3). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Вариант № 2
1.
На рисунке изображен график производной функции. Найдите абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.
2.
На рисунке изображён график производной функции определенной на интервале (−8; 9). Найдите количество точек минимума функции принадлежащих отрезку [−4; 8].
3.
На рисунке изображен график производной функции y=f(x), определенной на интервале (−7; 4). Найдите промежутки убывания функции .
В ответе укажите сумму целых точек, входящих в эти промежутки.
4.
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].
Тест «Геометрический смысл производной».
Вариант № 3
1.
На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
2.
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
3.
На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек экстремума функции на отрезке
4.
Функция y = f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если f (−5) ≥ f (5).
Тест «Геометрический смысл производной».
Вариант № 4.
На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наименьшее значение?
На рисунке изображён график производной функции . На оси абсцисс отмечены шесть точек: , , , , . Сколько из этих точек лежит на промежутках возрастания функции
На рисунке изображен график производной функции. Найдите абсциссу точки, в которой касательная к графику параллельна прямой или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). В какой точке отрезка [−6; −1] функция f(x) принимает наибольшее значение?
Вариант № 5.
1.
На рисунке изображен график функции y=f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
2.
На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке
3.
На рисунке изображён график функции и восемь точек на оси абсцисс: , , , , . В скольких из этих точек производная функции положительна?
4.
На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
Вариант № 6.
1.
На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна.
2.
На рисунке изображен график функции
, определенной на интервале (-3;11) . Найдите количество точек, в которых касательная к графику функции параллельна прямой y = — 11
3.
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссойx0. Найдите значение производной функции f(x) в точке x0.
4.
.
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
Вариант № 7.
1.
На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
2.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссойx0. Найдите значение производной функции f(x) в точке
3.
На рисунке изображен график производной функции , определенной на интервале . Определите количество целых точек, в которых производная функции положительна
4.
На рисунке изображен график функции y=f(x), определенной на интервале (−5; 7). Найдите сумму точек экстремума функции f(x).
Вариант № 8.
1.
На рисунке изображён график функции и двенадцать точек на оси абсцисс: , , , , . В скольких из этих точек производная функции отрицательна?
2.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
3.
На рисунке изображен график функции
y=f(x)
. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
f’
(8).
4.
На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите f'(10).
Вариант № 9.
1.
На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
2.
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].
3.
На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наименьшее значение?
4.
На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна.
5.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
6.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x − 19 или совпадает с ней.
7.
На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
8.
На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.