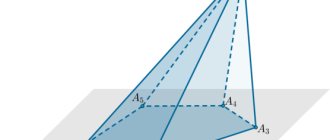
Lesson on the topic: “Prism and its elements. Prism surface area"

Elements of a triangular prism

Triangles ABC and A1B1C1 are the bases of a prism .

Quadrilaterals A1B1BA, B1BCC1 and A1C1CA are the lateral faces of the prism .

The sides of the faces are the edges of the prism (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), a triangular prism has 9 faces in total.

The height of a prism is the perpendicular segment that connects the two faces of the prism (in the figure it is h).

The diagonal of a prism is a segment that has ends at two vertices of the prism that do not belong to the same face. For a triangular prism such a diagonal cannot be drawn.

The base area is the area of the triangular face of the prism.

The lateral surface area of a prism is the sum of the areas of the quadrangular faces of the prism.

Independent work. "Prism. Rectangular parallelepiped"

Option 1

1.The base of a right prism is a right triangle with legs 6 and 8 cm. The diagonal of the side face containing the hypotenuse of the triangle is 26 cm. Find: the height of the prism, the area of the lateral surface of the prism. The total surface area of the prism.

2.The side of the base of a rectangular parallelepiped is 2 and 3 cm, and the diagonal is 7 cm. Find the lateral surface of the parallelepiped.

Option 2

1. The base of a right prism is a right triangle with a hypotenuse of 20 cm and a leg of 16 cm. The diagonal of the side face containing the second leg of the triangle is 13 cm. Find: height of the prism, lateral surface area, total surface area.

2. The base of a right parallelepiped is a parallelogram with sides of 5 and 8 cm and an acute angle. The total surface of a parallelepiped is Find its height.

Independent work “Pyramid”

Option 1

1.The base of the pyramid is an isosceles triangle with a side of 5 cm and a base of 6 cm. All dihedral angles at the base of the pyramid are equal. Find the total surface of the pyramid.

2. The side of the base of a regular quadrangular pyramid is 4 cm, and the apothem forms an angle with the plane of the base. Find: the height of the pyramid; lateral surface area of the pyramid.

Option 2

1.The base of the pyramid is a right triangle with sides 6 and 8 cm. All dihedral angles at the base of the pyramid are equal. Find the total surface of the pyramid.

2. The height of a regular quadrangular pyramid is 4 cm, and its apothem forms an angle with the height. Find the area of the base of the pyramid, the lateral surface of the pyramid

Test No. 12 “Polyhedra”

Option 1

1. At the base of a right triangular prism lies a right triangle with legs 8 cm and 6 cm. The lateral surface area is 120 cm2. Find the height of the prism.

2. The sides of the base of a right parallelepiped are 3 cm and 5 cm, the acute angle is 600. The major diagonal of the parallelepiped is 10 cm. Find the height of the parallelepiped.

3. The base of the pyramid МАВСD is the square ABCD. MV is the height of the pyramid and MV = AB = 4 cm. Find the area of the MDC face.

4. The height of a regular quadrangular pyramid is cm, and its lateral edge is cm. Find: a) the lateral surface of the pyramid, b) the dihedral angle at the base.

Option 2

1. The lateral edge of a regular quadrangular prism is equal to , and the diagonal of the side face is . Find the lateral surface of the prism.

2. The side of the base of a regular quadrangular prism is equal to , and the diagonal of the side face is . Find the lateral surface of the prism.

3. The base of the pyramid CABCD is the square ABCD. MV is the height of the pyramid and MV = AB = 7 cm. Find the area of the face KDC.

4. The height of a regular quadrangular pyramid is cm, and its lateral edge is cm. Find: a) the lateral surface of the pyramid, b) the dihedral angle at the base.

Find the derivative of the function: 1. 2. 3. 4. 5. 6. 7.

Basic formulas for calculating a triangular prism

Volume of a triangular prism

To find the volume of a triangular prism, you need to multiply the area of its base by the height of the prism.

Prism volume = base area x height

V=Sbas. h

Prism lateral surface area

To find the lateral surface area of a triangular prism, you need to multiply the perimeter of its base by its height.

Lateral surface area of a triangular prism = base perimeter x height

Sside=Pmain.h

Total surface area of the prism

To find the total surface area of a prism, you need to add its base area and lateral surface area.

since Sside=Pomain.h, we get:

Sfull.=Pbas.h+2Sbas

A regular prism is a straight prism whose base is a regular polygon.

Prism properties:

The upper and lower bases of the prism are equal polygons. The side faces of the prism have the shape of a parallelogram. The lateral edges of the prism are parallel and equal.

Tip: When calculating a triangular prism, you must pay attention to the units used. For example, if the base area is indicated in cm2, then the height should be expressed in centimeters and the volume in cm3. If the base area is in mm2, then the height should be expressed in mm, and the volume in mm3, etc.

Option 3

In a regular triangular prism ABCA1B1C1 AA1 = 4 cm, AB = . Find the volume of the prism.
Find the radius r of the base of the cylinder if h = 10 cm.
The base of a right prism is a right triangle with a hypotenuse of 10 cm and a leg of 6 cm. The larger leg of the triangle at the base of the prism is equal to the diagonal of the smaller of the side faces. Find
: 1) prism height; 2) the total surface area of the prism; 3) volume of the prism.
The diagonal of the axial section of the cylinder is 8 cm and inclined to the plane of the base at an angle of 30º. Find: 1)
r ; 2) h ;
3) base area; 4) the area of the lateral surface of the cylinder; 5) total surface area of the cylinder; 6) cylinder volume.
A part is lowered into a cylindrical vessel containing 6 liters of water. At the same time, the liquid level in the vessel rose 1.9 times. What is the volume of the part? Express your answer in liters.
Water was poured into a cylindrical vessel. The liquid level turned out to be 16 cm. The part was completely immersed in water. At the same time, the liquid level in the vessel rose by 13 cm. What is the volume of the part? Express your answer in .
In a cylindrical vessel, the liquid level reaches 48 cm. At what height will the liquid level be if it is poured into a second cylindrical vessel, the diameter of which is 4 times larger than the diameter of the first? Express your answer in centimeters.
At the base of a straight prism lies a right triangle with legs 10 and 16. The lateral edges are equal. Find the volume of the cylinder circumscribed around this prism.
At the base of a straight prism lies a square with side 4. The lateral edges are equal. Find the volume of the cylinder circumscribed around this prism.
Find the volume V
part of the cylinder shown in the figure. Please indicate in your answer.

Geometry-11

Geometry test. Grade 11. Topic: "Prism"

Test: “Prism”

Option 1

1).The diagonal of a regular quadrangular prism is inclined to the plane of the base at an angle of 600. Find the total surface of the prism if the diagonal of the base is 4 √2 cm.

2).At the base of a straight prism lies a rectangle with sides 6 cm and 8 cm. The height of the prism is 5 cm. Find the total surface of the prism.

3) Find the side of the base and the height of a regular quadrangular prism if its total surface area is 40 cm2 and its side surface is 32 cm2. 4) In a right parallelepiped with a height of √14 m, the sides of the base are 3 m and 4 m, the diagonal AC is 6 m. Find the area of the diagonal section of the parallelepiped passing through vertices B and D.

5) Find the diagonal of a rectangular parallelepiped based on its three dimensions: 7cm, 9cm and 11cm.

6) In a right parallelepiped, the sides of the base measuring 5 cm and 9 cm form an angle of 450, the side edge is 8 cm. Find the total surface of the prism.

7) In a regular quadrangular prism, the base area is 144 cm2 and the height is 10 cm. Find the area of the diagonal section. Option 2

1) Determine the total surface of a regular quadrangular prism if its diagonal is 14 cm and the diagonal of its side face is 10 cm.

2) The base of a straight prism is a rhombus. The diagonals of the prism are 8 cm and 5 cm, the height is 2 cm. Find the total surface of the prism.. 3) Find the side of the base and the height of a regular quadrangular prism if its lateral surface is 8 cm2 and the total is 40 cm2. 4) In a right parallelepiped with a height of √15 m, the sides of the base are 2 m and 4 m, the diagonal AC is 5 m. Find the area of the diagonal section of the parallelepiped passing through vertices B and D.

5) Find the diagonal of a rectangular parallelepiped based on its three dimensions: 6cm, 8cm and 12cm.

6) In a right parallelepiped, the sides of the base measuring 7 cm and 8 cm form an angle of 600, the side edge is 6 cm. Find the total surface of the prism.

7) In a regular quadrangular prism, the base area is 121 cm2 and the height is 8 cm. Find the area of the diagonal section.

——————————————————————————————————————————— Test: “Prism”