Practical work in mathematics on the topic "Polyhedra and their surfaces"

Practical work in mathematics on the topic “Polyhedra and their surfaces”

Section 10 . Polyhedra

Subject. Polyhedra and their surfaces.

Learning objective:

Know the formulas for calculating the lateral and total surface area of a prism, pyramid, parallelepiped and be able to apply them to solve problems.

Learning Objectives:

educational:

— generalize knowledge about polyhedra and their elements;

- repeat the formulas for calculating the surface areas of a rectangular parallelepiped, prism, pyramid;

— consolidate practical skills in calculating the surface areas of polyhedra;

— expand knowledge in the field of mathematics, show its applied nature;

developing:

— development of cognitive interest, logical thinking, spatial imagination and research abilities;

— development of computing skills, key competencies, abilities to compare, analyze, and justify the choice made;

educational:

— fostering responsibility, the ability to work in a team, and make independent decisions;

— show the significance of knowledge, the possibility of its application in practice.

Occupation availability:

1. Educational and methodological literature:

L.S. Atanasyan et al., Geometry. 10-11 grades – M.: Education, 2014.

2.Workbook: checkered

3. Handouts (task cards, according to the number of students).

4.Calculator: simple.

5.Handle.

6. Simple pencil.

7.computer,

8.multimedia projector,

9.screen.

Brief theoretical and educational-methodical

Practical work “Pyramid. Prism"

Practical work

On topic: "Pyramid"

Goals:

consolidation of concepts: pyramid, lateral and full surface area of the pyramid; education of cognitive activity, show the possibility of using the pyramid in various areas.

Guidelines

Pyramid

- a polyhedron, the base of which is a polygon, and the remaining faces are triangles having a common vertex. Based on the number of corners of the base, pyramids are classified as triangular, quadrangular, etc.

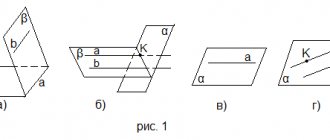
inclined straight line

Elements of the pyramid.

– height of the pyramid

DV, DS, YES

- side edges - common sides of the side faces;

TWO, DAS, ICE

- side faces - triangles converging at the top of the pyramid

DK, D L
- apothem
- the height of the side face of a regular pyramid, drawn from its vertex [ℓ];
D N
is the height of the pyramid.

The pyramid is called correct

, if its base is a regular polygon, and its vertex is projected to the center of the base. Then it has the following properties:

the lateral edges of a regular pyramid are equal; in a regular pyramid, all lateral faces are equal isosceles triangles; in any regular pyramid you can both fit and describe a sphere around it;

Rectangular pyramid

A pyramid is called rectangular if one of the side edges of the pyramid is perpendicular to the base. In this case, this edge is the height of the pyramid.

Truncated pyramid

A truncated pyramid is a polyhedron enclosed between the base of the pyramid and a cutting plane parallel to its base.

Side surface

is the sum of the areas of the side faces.

To find the lateral surface in a regular pyramid, you can use the formula:

Sb.p.= 1/2•Р•ℓ, where Р is the perimeter of the base.

Full surface

is the sum of the lateral surface area and the base area.

To find the total surface in a regular pyramid, you can use the formula:

Sp.p. = 1/2•Р•ℓ+Sbas.

Option 1

. How many edges does a hexagonal pyramid have: a)6; b)12; c)18; d)24;

. What is the smallest number of faces a pyramid can have: a)5; b)4 c)10; d)6

. Confirm or deny the following statements: Yes^no

a) A polyhedron made up of n-triangles is called a pyramid; b) A pyramid is called regular if its base is a regular polygon; c) The height of the side face of a regular pyramid, drawn from its vertex, is called apothem;

.
Task.
The roof of the tower has the shape of a regular quadrangular pyramid, with a side of the base equal to 12 m and a height of 18 m. How many tiles will be needed to cover this roof if each tile has the shape of a rectangle with sides of 22 cm and 18 cm.

Option 2

. How many faces does a hexagonal pyramid have: a)6; b)7; at 8; d)10;

.
What is the smallest number of edges a pyramid can have: a)6; b)5; at 4; d)7; 3
Confirm or refute the following statements: Yes ^ no a) The height of the pyramid is called the height of the face; b) The area of the lateral surface of the pyramid is equal to the product of the perimeter of the base and the height; c) A pyramid is called regular if its base is a regular polygon;

.
Tasks
. One of the most grandiose structures of antiquity - the Cheops pyramid - has the shape of a regular quadrangular pyramid with a height of 150 m and a side edge of 220 m. Find the area of the lateral surface

Option 3

. How many edges does a quadrangular pyramid have: a)6; b)12; at 8

. What is the smallest number of faces a pyramid can have: a)5; b)4 c)10; d)6

.Confirm or refute the following statements: Yes ^ no a) Is there a quadrangular pyramid whose opposite side faces are perpendicular to the base? b) The height of a pyramid is a perpendicular drawn from the top to the base. c) The common point of the lateral faces of the pyramid is called the vertex

.
Task
. The roof is in the shape of a pyramid with a square base of 4.5 m x 4.5 m and a height of 4 m. How many sheets of iron measuring 70 cm x 140 cm are needed to cover the roof if 10% of the roof area is to be added to waste?

Practical work

On topic: "Prism"

Goals:

consolidation of concepts: rectangular parallelepiped, linear dimensions, diagonal, lateral and full surface area of a prism; promote interest in mathematics and its applications.

Guidelines

Prism

- a polyhedron, two of whose faces are polygons lying in parallel planes, and the remaining faces are parallelograms having common sides with these polygons.

Types of prisms.

A prism whose base is a parallelogram is called parallelepiped
.
Straight prism
is a prism whose side ribs are perpendicular to the plane of the base.
Other prisms are called oblique prisms
.
Correct prism
is a right prism whose base is a regular polygon. The lateral faces of a regular prism are equal rectangles.

straight prism inclined prism

Prism properties:

The bases of the prism are equal polygons.
The lateral faces of the prism are parallelograms.
The lateral edges of the prism are parallel and equal.

Lateral surface area of a straight prism

:
S b.p. = P • H
where P is the perimeter of the base of the prism (the sum of all sides of the base), H is the height of the prism.

Total surface area of the prism

equal to the sum of the area of its lateral surface and twice the area of the base:
S p.p. = P • H +2 • S main
The square of the diagonal of a rectangular parallelepiped is equal to the sum of the squares of its three linear dimensions: d 2
= a 2 + b 2 + c 2
Tasks for independent work:

Option 1

. How many edges does a hexagonal prism have?

Answer: a)18, b)24, c)12.

.Choose the correct statement.

a) a prism is called regular if its bases are regular polygons;

b) a triangular prism has two diagonals;

c) the height of the prism is equal to its lateral edge;

3.Task

. Find the diagonal length of a rectangular parallelepiped if its dimensions are 2m, 3m, 5m.

.
Task.
The collector ordered an aquarium in the shape of a regular quadrangular prism. How many square meters of glass are needed to make an aquarium if the side of the base is 70 cm and the height is 60 cm?

Option 2

.How many faces does a hexagonal prism have?

Answer: a)6, b)8, c)10

. Choose the correct statement.

a) the area of the total surface of a prism is called the sum of the areas of its lateral faces and base;

b) a triangular prism has no diagonals;

c) the height of a straight prism is equal to its lateral edge;

.
Task.
Find the diagonal length of a rectangular parallelepiped if its dimensions are 3cm, 4cm, 5cm.

4. Problem

It is necessary to make a box with a lid for storing potatoes in the shape of a straight prism 0.7 m high. At the base of the prism is a rectangle with sides 0.4 m and 0.6 m. How much plywood is needed to make the box?

Option 3

.How many faces does a quadrangular prism have?

Answer: a)6, b)8, c)10

. Choose the correct statement.

a) An n – carbon prism has 2 n edges;

b) the area of the total surface of a prism is called the sum of the areas of its lateral faces;

c) a triangular prism has three diagonals;

.
Task.
How many sheets of 8-wave slate, 1750*1130 mm in size, are needed to cover the roof of a building 10 m long? The pediment has the shape of an isosceles right triangle with a hypotenuse of 10 m and a leg of 7 m.

.
Task.
It is necessary to cover a room with wallpaper of the “matting” type, the length of which is 6 m, width 4 m, height 3 m, the area of windows and doors is 1/5 of the total area of the walls. How many rolls of wallpaper are needed to cover a room if the length of the roll is 12 m and the width is 50 cm?

Mysteries of the pyramids

Firstly, there are mysteries associated with the process and technology of building the pyramids. During expeditions and archaeological research, no descriptions or drawings related to the construction of the pyramids were found. Assumptions about the course and technology of construction of the pyramids were made based on existing knowledge about the construction technologies of ancient civilizations.

It was assumed: the approximate number of workers is hundreds of thousands of people; methods of transporting stone blocks - along the Nile during the period of flood, when the area of the water surface significantly increased and lengthened, allowing transportation to the maximum distance; as well as possible types of tools, devices and mechanisms. However, in all these questions there are a lot of stretches and unsupported assumptions: for example, it is known that the Egyptians did not know iron, bronze, alloys, they used only stone and copper tools, primitive plumb lines, levels, triangles and other measuring instruments.

But at the same time, the two most difficult problems - the ideal alignment of the base for the building and maintaining the angle of inclination of the cornerstones so that the edges merge at a great height - were carried out at the highest and most precise mathematical level. It is simply impossible to accomplish this task with such an imperfect range of instruments at hand. It seems equally impossible to transport and, to an even greater extent, lift and install stone blocks with pinpoint precision, despite the fact that the builders had neither cranes nor other modern construction mechanisms.

Secondly, the generally accepted point of view on the purpose of the pyramids - that they are simply grandiose tombs for the pharaohs - does not explain the fact that the body of a pharaoh was not found in any pyramid, nor the fact that in addition to the so-called burial chamber in the pyramids , as a result of modern research, a large number of different empty rooms of unknown purpose have been found, corridors ending in dead ends, underground chambers, etc.

And thirdly, there are features of the pyramids that go far beyond the level of development of civilization at that time and the theory about the funerary purpose of these structures.

Mathematical : the geometric structure of the pyramids contains the principle of the “golden ratio”, the number “pi” and various other features from the field of trigonometry and higher mathematics.

Astronomical : high-precision astronomical orientation of the pyramids to the cardinal points; they have moves oriented strictly towards certain stars.

Geological : in addition to local materials, granite (presumably brought from an area 900 km upstream of the Nile) and basalt of unknown origin were used in construction.

Technological : during construction, slabs weighing more than 200 tons were repeatedly used, as well as millions of limestone blocks weighing 2.5 tons; Grinding methods with unknown tools were used, the accuracy and cleanliness of the drilled holes does not correspond even to modern construction drills and drills, etc. (4)

Crossword puzzle with questions and answers on geometry for grade 7: Polygons and polyhedra

Crossword and game for 7th grade on the topic “Polygons and Polyhedra”
Author: Yulia Ryamilyevna Pestova, MBOU “Secondary School No. 76”, Ulyanovsk Description of the material: I offer you material that can be used to consolidate the knowledge of 7th grade students on the topic “Polygons” and polyhedra."
The composition includes a crossword puzzle and the game “Bigger and Faster”, which I am sure will interest the children and help unite the collective spirit. Crossword and game “More and faster” on the topic “Polygons and polyhedra”
Goal: generalization and systematization of knowledge on the topic “Polygons and polyhedra” Objectives: - to promote the development of intelligence, logical thinking, mathematical erudition of students - to cultivate cognitive interest in students - to be able to work in pairs and collectively
Crossword

Questions: 1. If the figures are made up of identical parts, then they are called...? 2. A parallelogram with all sides equal? 3. If you draw two pairs of parallel lines, then when they intersect, a quadrilateral is formed, the opposite sides of which are parallel. What is this quadrilateral called? 4. An angle whose value is greater than 90 degrees, but less than 180 degrees? 5. A flat figure formed by a closed series of straight segments? 6. Side of the polyhedron? 7. A polygon in which all sides and all angles are equal is called...? 8. A segment connecting 2 vertices that do not lie on the same face? 9. ... symmetry of a parallelogram - the point of intersection of its diagonals? 10. A body whose boundary consists of pieces of planes (polygons)? 11. From Ancient Greece the word “rhombus” came to us, meaning “…”, the silhouette of which really has the shape of a rhombus. Answers: 1. equipartite 2. rhombus 3. parallelogram 4. obtuse 5. polygon 6. edge 7. regular 8. diagonal 9. center 10. polyhedron 11. top Main word: triangle
Game “Bigger and Faster”
Student task: the class is divided for 2 teams. Each team must try to get from C to F as quickly as possible (you can only walk down, left, right) and have at least 30 points in total, otherwise the victory goes to the other team. If a team cannot answer a question, it goes to the other team. If this team answers it, then it remains in its same place, but adds to its total the points at which the question was valued.

Questions: 5 points: 1. The word “parallelogram” comes from the Greek “...” (depicted as parallel) 2. What property do the diagonals of a parallelogram have (the intersection point is divided in half) 3. How does a rectangle differ from a square (its sides are pairwise equal, and a square has all sides equal) 4. Name 5 regular polyhedra (tetrahedron, hexahedron, octahedron, icosahedron, dodecahedron) 5. Write a formula for calculating the area of a right triangle with legs a and b (S = 1/2ab) in 4 points: 1. What is the center of symmetry of a parallelogram? (the point of intersection of its diagonals) 2. Name 3 types of regular polygons (equilateral triangle, square, hexagon, etc.) 3. What important property do all the vertices of a regular polygon have (lie on the same circle) 4. Which polygon is called regular? (all sides and angles of which are equal) 5. This word from Greek means “sawn piece” (prism) worth 3 points: 1. If a hexagon is regular, then each of its angles is equal to ... (120 degrees) 2. What property do the diagonals of a rhombus have ( they are perpendicular to each other) 3. What figure is called a regular polyhedron (all faces of which are equal) 4. A prism, all faces of which are rectangles (parallelepiped) 5. Among the faces of a prism there are ... (side faces and bases) in 2 points: 1. Main property isosceles triangle (the angles at the base are equal) 2. A parallelogram, all sides of which are equal (rhombus) 3. How many axes of symmetry does a regular triangle have (3) 4. If the figures are made up of identical parts, then they ... (equally proportioned) 5. Two figures, having the same areas are called ... (equal) for 1 point: 1. A quadrilateral with equal sides and angles (square) 2. The sum of the angles of a triangle is ... (180 degrees) 3. What is the size of the angle of an equilateral triangle (60 degrees)

We recommend watching:

An open lesson in mathematics in the 7th grade of a correctional school. An extracurricular event in mathematics in grades 6-7. Scenario Extracurricular Math Activities, Grades 7-9 Lesson notes for a 7th grade algebra lesson. Multiplying a monomial by a polynomial

Practical work “Regular polyhedra”

Developed by: Marina Aleksandrovna Rudakova, mathematics teacher

Place of work: Baikal branch of GAPOU SO "Slobodoturinsky Agrarian-Economic College"

Practical work “Regular polyhedra”

Target:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Tasks:

Task No. 1.

Complete the crossword puzzle “Regular polyhedra”


1
2	3
4
5
6
7	8
9	10
11
12
		13

Horizontally:

Correct hexagon.
4.
Flat polygons that make up the surface of a polyhedron.
6 .
Regular twenty-sided.
7.
Regular dodecahedron.
9.
What polygon does the cube consist of?
11.
A convex point connecting the polygons of a polyhedron.
12.
An ancient Greek philosopher who described in detail regular polyhedra.
13.
Regular octahedron.

Vertically:

Triangular pyramid.
3 .
Side of a polyhedron face.
5.
A body whose surface consists of a finite number of flat polygons.
8.
Author of the theorem (formula)
В+Г=Р+2,
showing the relationship between the vertices, faces and edges of a convex polyhedron.
10.
What polygon does the tetrahedron and octahedron consist of?

Task 2.

Conduct research on the Platonic solids:

1) Count the number of vertices, edges and faces.

2) Find the relationship between them using Euler’s theorem В-Р+Г=2.

3) How many Platonic solids have we got for which Euler’s theorem holds?

4) What are the faces of the Platonic solid under study?

1) tetrahedron:  -  +  = , consists of _________________________

2) hexahedron:  -  +  = , consists of _________________________

3) octahedron:  -  +  = , consists of _________________________

4) icosahedron:  -  +  = , consists of _________________________

5) dodecahedron:  -  +  = , consists of _________________________

3 task.

Level 1

You need to calculate the amount of paint for the ceiling in the shape of a square with a side of 6m.

Solution:

1) For the ceiling, the area will be equal to: the length of the room multiplied by the width.

_______________________________________

2) If the label of the can indicates paint consumption for a single-layer coating of 100 g/m2, then for 36 m2 the consumption will be equal to

_______________________________________

3) If the paint is packaged in 2.5 kg cans, how much should I buy?

_______________________________________

4) If paint is available for sale only in 1 kg cans, then how many cans will you have to buy?

_______________________________________

Practical lesson on the topic "Elements of the pyramid" methodological development on the topic