Problems on the topic "Area" 8th grade
Problems on the topic “Area”
1.Find the area of the triangle shown in the figure.
2. Find the area of the triangle shown in the figure.
3. The side of an isosceles triangle is 34 and the base is 60. Find the area of this triangle.
4. Find the area of a right triangle if its side and hypotenuse are 28 and 100, respectively.
5. Find the area of a right triangle if its side and hypotenuse are 40 and 85, respectively.
6. In a right triangle, the hypotenuse is 70, and one of the acute angles is 45∘. Find the area of the triangle.
7. The side of an isosceles triangle is 25 and the base is 30. Find the area of this triangle.
8. In a right triangle, the hypotenuse is 82, and one of the acute angles is 45∘. Find the area of the triangle.
9. The side of an isosceles triangle is 25 and the base is 48. Find the area of this triangle.
10. Find the area of the figure
. Find the area of the triangle shown in the figure
11. In a right triangle, the hypotenuse is 4, and one of the acute angles is 45∘. Find the area of the triangle.
12. In a right triangle, the hypotenuse is 8, and one of the acute angles is 45∘. Find the area of the triangle.
13.The side of an isosceles triangle is 15 and the base is 18. Find the area of this triangle.
14. Find the area of a square circumscribed around a circle of radius 83.
15.
16. A rectangle was cut out of a square (see picture). Find the area of the resulting figure.
17. The perimeter of an isosceles triangle is 196 and the base is 96. Find the area of the triangle.
18. Find the area of the parallelogram shown in the figure.
19. In a triangle with sides 18 and 9, the altitudes are drawn to these sides. The height drawn to the first side is equal to 1. What is the height drawn to the second side?
20. Area of parallelogram ABCD
is equal to 6. Point
E
is the midpoint of side
AB
.
Find the area of the trapezoid EBCD
.
21. The side of a rhombus is 9, and the distance from the center of the rhombus to it is 1. Find the area of the rhombus.
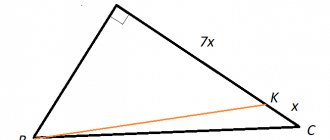
22. In a triangle with sides 8 and 2, the altitudes are drawn to these sides. The height drawn to the first side is equal to 1. What is the height drawn to the second side?
23. In a triangle with sides 2 and 10, the altitudes are drawn to these sides. The height drawn to the first side is 5. What is the height drawn to the second side?
24. The perimeter of an isosceles triangle is 162 and the base is 72. Find the area of the triangle.
25. In a triangle with sides 15 and 5, the altitudes are drawn to these sides. The height drawn to the first side is equal to 1. What is the height drawn to the second side?
26. The area of a rhombus is 27 and the perimeter is 36. Find the height of the rhombus.
27. Area of parallelogram ABCD
is equal to 56. Point
E
is the middle of side
CD
.
Find the area of the trapezoid AECB
.
28. Find the area of a figure
29. Find the area of a figure
30. Find the area of a figure
31. In the trapezoid ABCD
AD
=3,
BC
=1, and its area is 12. Find the area of triangle
ABC
.
32.
33. Find the area of a figure
34. Find the area of a figure
35. Find the area of a figure
36. Height BH
A rhombus
ABCD
divides its side
AD
into segments
AH
=5 and
HD
=8. Find the area of the rhombus.
37. Find the area of a figure
38. The side of a rhombus is 50 and the diagonal is 80. Find the area of the rhombus.
39. Find the area of a figure
40. Find the area of a rhombus if its diagonals are 14 and 6.
41. In a right triangle, one of the legs is equal to 17, and the acute angle adjacent to it is equal to 45∘. Find the area of the triangle.
42. Find the area of a square if its diagonal is 1.
43. In a rectangle, one side is 96 and the diagonal is 100. Find the area of the rectangle.
44. Area of parallelogram ABCD
is equal to 176. Point
E
is the middle of side
AD
.
Find the area of the trapezoid AECB
.
45.
46. The perimeter of an isosceles triangle is 288 and the base is 128. Find the area of the triangle.
47. The perimeter of an isosceles triangle is 200 and the base is 96. Find the area of the triangle.
48. Find the area of the trapezoid
Answers:
Geometry 8th grade “Solving problems on the topic Area”
And at the end of 9th grade you will also have to take the State Exam, where you will meet problems on checkered paper. For example, this (on the screen is a problem about a rectangle).Which one of you can explain to us how to solve it?
Let's solve a few more tasks from the FIPI open bank.
Such problems were included in the main work of the ancient Greek mathematician Euclid, the textbook “Principia”; people studied geometry from this textbook for two millennia.
So we could study with you at the Euclid school
Evaluate your performance on the self-assessment form
Another famous ancient Greek philosopher and geometer is Pythagoras. What is Pythagoras famous for?
State and write down the Pythagorean theorem on the board and in your notebook. How to find the hypotenuse using the theorem, how to find an unknown leg?
Solve problems using the Pythagorean theorem.
Pythagoras was also the champion of the ancient Olympic Games.
Let's warm up a bit too
Pythagoras organized his Pythagorean Order and the School of Philosophers and Mathematicians. They were accepted there with great ceremonies and after long trials. The school had very serious discipline, there were strict rules - commandments. Let's find out which ones?
Solve the problems correctly and compose the text of the commandments. The teacher (students in rows) distributes cards with tasks. The teacher instructs.
Card I.
No. 1. The legs of a right triangle are 3 and 4 cm. Calculate its hypotenuse.
| No. 2. The diagonal of rectangle ABCD is 10 cm. Side AB = 8 cm. Calculate side BC. | |
| Answers to problem No. 1 | Answers to problem No. 2 |
| 5 – don’t chase happiness | 4 – it is present near you |
| 6 – don’t run after happiness | 6 – it is always within you |
Answer : Don’t chase happiness, it is always within you.
Card II.
| No. 1. Calculate the leg of a right triangle if the other leg is 8 and the hypotenuse is 10 cm. | No. 2. The sides of the rectangle are 12 cm and 5 cm. Calculate the length of the diagonal. |
| Answers to problem No. 1 | Answers to problem No. 2 |
| 4 – formulas | 13 – rule the world |
| 6 – numbers | 14 – rule everything |
Answer: Numbers rule the world.
Cards for III
| No. 1. Calculate the leg of a right triangle if its other two sides are 15 and 17 cm. | No. 2. Find the lateral side of an isosceles triangle if the base is 8 cm and the height lowered to the base is 3 cm. |
| Answers to problem No. 1 | Answers to problem No. 2 |
| 8 – either be silent | 5 – either say what is more valuable than silence |
| 64 – keep quiet if you want | 6 – or talk about what is interesting to everyone |
Answer : Either remain silent, or say what is more valuable than silence.
After completion, go up the rows, what commandments were there in the Pythagorean school? (Pin to board)
Fill out the self-assessment form, maximum score -3
There are often problems in which you need to prove that a triangle is right-angled. Knowledge of what theorem will be useful to us in this case?
Let's remember the converse theorem of Pythagoras
Name triplets of numbers that support this statement.
Compose three Pythagorean triplets on the blanks.
After students answer, display a slide
Pythagoras was not only a great geometer, but also an ancient philosopher; he believed that “Numbers rule the world.” Do you agree with this statement? It’s not numbers that rule the world, but we use them to solve many practical problems, such as this one
—
Calculate the cost of the laminate that needs to be laid in a room 5.5 m long and 4.5 m wide, if one board is 20 cm x 130 cm. The cost of one board is 156 rubles.
| Room length in cm | Room width in cm | Floor area of the room in cm2 | ||
| 550 | 450 | |||
| Length of the board in cm | Board width in cm | Area of one plank in cm2 | Number of planks | The cost of the entire laminate is in rubles. |
| 130 | 20 |
Independent work on geometry in grade 8 on the topic “Areas of figures”
1 option
1. The side of a parallelogram is 21 cm, and the height drawn to it is 15 cm. Find the area of the parallelogram.
2. The side of a triangle is 5 cm, and the height drawn to it is twice the side. Find the area of the triangle.
3. In a trapezoid, the bases are 6 and 10 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid
Option 2
1. The side of a parallelogram is 17 cm, and its area is 187 cm². Find the height drawn to this side.
2. The side of a triangle is 18 cm, and the height drawn to it is 3 times less than the side. Find the area of the triangle.
3. In a trapezoid, the bases are 4 and 12 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid.
1 option
1. The side of a parallelogram is 21 cm, and the height drawn to it is 15 cm. Find the area of the parallelogram.
2. The side of a triangle is 5 cm, and the height drawn to it is twice the side. Find the area of the triangle.
3. In a trapezoid, the bases are 6 and 10 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid
Option 2
1. The side of a parallelogram is 17 cm, and its area is 187 cm². Find the height drawn to this side.
2. The side of a triangle is 18 cm, and the height drawn to it is 3 times less than the side. Find the area of the triangle.
3. In a trapezoid, the bases are 4 and 12 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid.
1 option
1. The side of a parallelogram is 21 cm, and the height drawn to it is 15 cm. Find the area of the parallelogram.
2. The side of a triangle is 5 cm, and the height drawn to it is twice the side. Find the area of the triangle.
3. In a trapezoid, the bases are 6 and 10 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid
Option 2
1. The side of a parallelogram is 17 cm, and its area is 187 cm². Find the height drawn to this side.
2. The side of a triangle is 18 cm, and the height drawn to it is 3 times less than the side. Find the area of the triangle.
3. In a trapezoid, the bases are 4 and 12 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid.
1 option
1. The side of a parallelogram is 21 cm, and the height drawn to it is 15 cm. Find the area of the parallelogram.
2. The side of a triangle is 5 cm, and the height drawn to it is twice the side. Find the area of the triangle.
3. In a trapezoid, the bases are 6 and 10 cm, and the height is equal to half the sum of the lengths of the bases. Find the area of the trapezoid
Option 2
1. The side of a parallelogram is 17 cm, and its area is 187 cm². Find the height drawn to this side.
All formulas for geometry. Areas of figures
To solve geometry problems, you need to know formulas—such as the area of a triangle or the area of a parallelogram—as well as simple techniques that we'll cover.
First, let's learn the formulas for the areas of figures. We have specially collected them in a convenient table. Print, learn and apply!
Of course, not all geometry formulas are in our table. For example, to solve problems in geometry and stereometry in the second part of the profile Unified State Exam in mathematics, other formulas for the area of a triangle are used. We will definitely tell you about them.
Did you find what you were looking for? Share with your friends!
But what if you need to find not the area of a trapezoid or triangle, but the area of some complex figure? There are universal ways! We will show them using examples from the FIPI task bank.
1. How to find the area of a non-standard figure? For example, an arbitrary quadrilateral? A simple technique - let's divide this figure into those that we know everything about, and find its area - as the sum of the areas of these figures.
Divide this quadrilateral with a horizontal line into two triangles with a common base equal to . The heights of these triangles are equal to and . Then the area of the quadrilateral is equal to the sum of the areas of the two triangles: .
Answer: .
2. In some cases, the area of a figure can be represented as the difference of some areas.
It is not so easy to calculate what the base and height of this triangle are equal to! But we can say that its area is equal to the difference between the areas of a square with a side and three right triangles. Do you see them in the picture? We get: .
Answer: .
3. Sometimes in a task you need to find the area of not the entire figure, but part of it. Usually we are talking about the area of a sector - part of a circle. Find the area of a sector of a circle of radius whose arc length is equal to .
In this picture we see part of a circle. The area of the entire circle is equal to . It remains to find out which part of the circle is depicted. Since the length of the entire circle is equal (since), and the length of the arc of a given sector is equal, therefore, the length of the arc is a factor of less than the length of the entire circle. The angle at which this arc rests is also a factor of less than a full circle (that is, degrees). This means that the area of the sector will be several times smaller than the area of the entire circle.
Answer: .