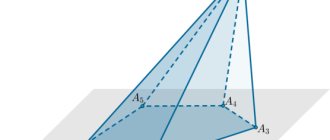
Урок по теме: «Призма и ее элементы. Площадь поверхности призмы"

Элементы треугольной призмы

Треугольники ABC и A1B1C1 являются основаниями призмы.

Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.

Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Самостоятельная работа. «Призма. Прямоугольный параллелепипед»

Вариант 1

1.Основание прямой призмы – прямоугольный треугольник с катетом 6 и 8 см. Диагональ боковой грани, содержащей гипотенузу треугольника, равна 26см. Найдите: высоту призмы, площадь боковой поверхности призмы. Площадь полной поверхности призмы.

2.Сторона основания прямоугольного параллелепипеда равна 2 и 3 см, а диагональ – 7см. Найдите боковую поверхность параллелепипеда.

Вариант 2

1. Основание прямой призмы — прямоугольный треугольник с гипотенузой 20 см, и катетом 16 см. Диагональ боковой грани, содержащей второй катет треугольника, равна 13см. Найдите: высоту призмы, площадь боковой поверхности, площадь полной поверхности.

2. Основание прямого параллелепипеда – параллелограмм со сторонами 5 и 8 см. и острым углом . Полная поверхность параллелепипеда равна Найдите его высоту.

Самостоятельная работа «Пирамида»

Вариант 1

1.Основание пирамиды -равнобедренный треугольник с боковой стороной 5 см. и основанием 6 см. Все двугранные углы при основании пирамиды равны . Найдите полную поверхность пирамиды.

2. Сторона основания правильной четырехугольной пирамиды равна 4см, а апофема образует с плоскостью основания угол Найдите: высоту пирамиды; площадь боковой поверхности пирамиды.

Вариант 2

1.Основание пирамиды – прямоугольный треугольник с катетом 6 и 8 см. Все двугранные углы при основании пирамиды равны Найдите полную поверхность пирамиды.

2. Высота правильной четырехугольной пирамиды равна 4 см, а ее апофема образует с высотой угол Найдите площадь основания пирамиды, боковая поверхность пирамиды

Контрольная работа №12 «Многогранники»

Вариант 1

1. В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 см и 6 см. Площадь боковой поверхности равна 120 см2. Найдите высоту призмы.

2. Стороны основания прямого параллелепипеда равны 3 см и 5 см, острый угол 600. Большая диагональ параллелепипеда равна 10 см. Найдите высоту параллелепипеда.

3. Основанием пирамиды МАВСD служит квадрат АВСD. МВ – высота пирамиды и МВ=АВ= 4 см. Найдите площадь грани МDС.

4. Высота правильной четырехугольной пирамиды равны см, а ее боковое ребро см. Найдите: а) боковую поверхность пирамиды, б) двугранный угол при основании.

Вариант 2

1. Боковое ребро правильной четырехугольной призмы равно , а диагональ боковой грани – . Найдите боковую поверхность призмы.

2. Сторона основания правильной четырехугольной призмы равна , а диагональ боковой грани . Найдите боковую поверхность призмы.

3. Основанием пирамиды КАВСD служит квадрат АВСD. МВ – высота пирамиды и МВ=АВ= 7 см. Найдите площадь грани KDС.

4. Высота правильной четырехугольной пирамиды равна см, а ее боковое ребро см. Найдите: а) боковую поверхность пирамиды, б) двугранный угол при основании.

Найдите производную функции: 1. 2. 3. 4. 5. 6. 7.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

или

V=Sосн . h

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

или

Sбок=Pосн.h

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как Sбок=Pосн.h, то получим:

Sполн.пов.=Pосн.h+2Sосн

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы:

Верхнее и нижнее основания призмы – это равные многоугольники. Боковые грани призмы имеют вид параллелограмма. Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.

Вариант 3

В правильной треугольной призме АВСА1В1С1 АА1 = 4 см, АВ = . Найдите объем призмы.
Найдите радиус r основания цилиндра, если h =10см.
Основание прямой призмы — прямоугольный треугольник с гипотенузой 10 см и катетом 6см.Больший катет треугольника в основании призмы равен диагонали меньшей из боковых граней. Найдите
: 1) высоту призмы; 2) площадь полной поверхности призмы; 3) объём призмы.
Диагональ осевого сечения цилиндра равна 8 см и наклонена к плоскости основания под углом 30º. Найдите: 1)
r; 2)h; 3) площадь основания; 4) площадь боковой поверхности цилиндра; 5) площадь полной поверхности цилиндра; 6)
объем цилиндра.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? Ответ выразите в литрах.
В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Чему равен объем детали? Ответ выразите в .
В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 16. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Найдите объем V
части цилиндра, изображенной на рисунке. В ответе укажите .

Геометрия-11

Контрольная работа по геометрии . 11 класс. Тема : » Призма»

Контрольная работа: « Призма»

Вариант 1

1).Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 600. Найдите полную поверхность призмы, если диагональ основания равна 4 √2 см.

2).В основании прямой призмы лежит прямоугольник со сторонами 6 см и 8 см. Высота призмы равна 5 см. Найдите полную поверхность призмы.

3) Найдите сторону основания и высоту правильной четырехугольной призмы, если площадь ее полной поверхности равна 40 см2, а боковая поверхность 32 см2 . 4) В прямом параллелепипеде с высотой √14 м стороны основания равны 3 м и 4 м, диагональ АС равна 6 м. Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины В и Д.

5)Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 7см, 9см и 11см.

6) В прямом параллелепипеде стороны основания величиной 5см и 9см образуют угол 450, боковое ребро равно 8см. Найдите полную поверхность призмы.

7) В правильной четырехугольной призме площадь основания равна 144см2, а высота 10см. Найдите площадь диагонального сечения. Вариант 2

1) Определить полную поверхность правильного четырехугольной призмы, если ее диагональ равна 14 см, а диагональ боковой грани равна 10 см.

2)Основанием прямой призмы служит ромб. Диагонали призмы равны 8 см и 5 см, высота равна 2 см. Найдите полную поверхность призмы.. 3)Найдите сторону основания и высоту правильной четырехугольной призмы, если ее боковая поверхность равна 8 см2 , а полная 40 см2 . 4)В прямом параллелепипеде с высотой √15 м стороны основания равны 2 м и 4 м, диагональ АС равна 5 м. Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины В и Д.

5)Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 6см, 8см и 12см.

6) В прямом параллелепипеде стороны основания величиной 7см и 8см образуют угол 600, боковое ребро равно 6см. Найдите полную поверхность призмы.

7) В правильной четырехугольной призме площадь основания равна 121см2, а высота 8см. Найдите площадь диагонального сечения.

——————————————————————————————————————————— Контрольная работа: « Призма»

Вариант 1

5)Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 7см, 9см и 11см.

5)Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 6см, 8см и 12см.

Вариант А1

Сторона основания правильной треугольной призмы равна 6см, а диагональ боковой грани равна 10 см. Найдите площадь боковой и полной поверхности призмы.
Основание прямой призмы – ромб со стороной 5 см и тупым углом 120°. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
Все боковые грани наклонного параллелепипеда – ромбы с острым углом 30°. Найдите площадь боковой поверхности параллелепипеда, если его высота равна 2 см, а боковое ребро образует с плоскостью основания угол 45°.

Вариант А2

Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.
Основание прямой призмы – ромб с острым углом 60°. Боковое ребро призмы равно 10 см, а площадь боковой поверхности – 240 см2 .Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
Две боковые грани наклонной треугольной призмы – ромбы с основным углом 30°, а третья боковая грань – квадрат. Высота призмы равна 4 см, а боковое ребро наклонено к плоскости основания под углом 45°. Найдите площадь боковой поверхности призмы.

Вариант Б1

Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
Боковая поверхность правильной четырехугольной призмы имеет площадь 16 дм2 . Диагональ основания призмы равна 4дм. Найдите площадь сечения призмы, проходящего через диагонали двух смежных боковых граней, имеющие общую вершину.
В наклонном параллелепипеде основание и одна из боковых граней – квадраты, плоскости которых образуют угол 30°, а площадь каждого из них равна 36см2. Найдите площадь полной поверхности параллелепипеда.