Ershova Goloborodko 9th grade independent and control work of the State Duma
Here are the answers to independent and test work in algebra and geometry, grade 9 Ershov Goloborodko. You can watch and read GDZ online (without downloading) from your computer and mobile devices.
ALGEBRA
Quadratic function C-1. Functions and their properties
S-2. Square trinomial C-3. Graph of a quadratic function
S-4*. Quadratic function: problems with parameters (independent homework) K-1. Quadratic function
S-6. Solving inequalities using the interval method
K-2. Solving inequalities
S-8*. Equations of higher degrees: solution methods, problems with parameters (independent homework) P-9. Solving systems of second degree equations
S-10. Solving problems using systems of equations. Graphic solution of systems
S-11*. Systems of rational equations (independent homework) K-3. Whole equations and systems of equations Arithmetic and geometric progressions P-12. Arithmetic progression. Formula nth term
S-13. Formula for the sum of n first terms of an arithmetic progression
K-4. Arithmetic progression
S-14. Geometric progression. Formula of the nth member of C-15. Formula for the sum of the first n terms of a geometric progression. S-16*. Combined progressive tasks (independent homework) K-5. Geometric progression
Degree with a rational indicator C-17. Even and odd functions. Function Y = *» C-18. The nth root and its properties
S-19. Definition and properties of degree with fractional exponent C-20. Transformation of power expressions with rational exponents K-6. Power with rational exponent
Trigonometric expressions and their transformations S-21. Definition of trigonometric functions
S-22. Properties of trigonometric functions. Radian measure of angle C-23. Trigonometric identities and their applications
S-24. Reduction formulas
K-7. Properties of trigonometric functions.
S-25. Addition formulas C-26. Double angle formulas
S-27. Formulas for the sum and difference of trigonometric functions
K-8. Addition formulas and their consequences
S-28*. Additional trigonometry problems (independent homework) K-9. Annual test
GEOMETRY (according to Pogorelov)
SP-1 figures Similarity transformation and its properties
SP-2. Signs of similarity of triangles
SP-3. Similarity of right triangles.
SP-4*. Similarity of triangles (independent homework) KP-1. Similarity of figures
SP-5. The inscribed angle theorem and its consequences
SP-6*. Application of the inscribed angle theorem and its consequences in problems (independent homework) Solving triangles SP-7. The cosine theorem. The ratio of diagonals and sides of a parallelogram
SP-8. Theorem of sines and its consequences
SP-9*. Theorems of cosines and sines (independent homework) KP-2. Solving triangles
KP-3. Polygons Areas of figures SP-13. Area of a rectangle, square, parallelogram
SP-14. Area of a triangle
SP-16*. Circle and polygon (independent homework) SP-17. Areas of similar figures. Area of a circle and its parts
SP-18*. Areas of figures (independent homework) KP-4. Areas of figures
KP-5. Annual test
GEOMETRY (according to Atanasyan)
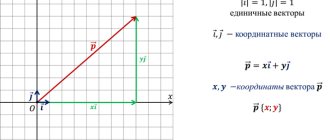
SA-1 coordinate method Vector coordinates
SA-2. The simplest problems in coordinates
SA-3.Equation of a circle
SA-4.Equation of straight line C-5*. Application of vectors and coordinates to problem solving (independent homework) KA-1. Coordinate method
Relationships between sides and angles of a triangle. Scalar product of vectors CA-6. Sine, cosine, tangent of angle
SA-9. Dot product of vectors
SA-10*. Solving triangles. Dot product (independent homework) KA-2. Relationship between sides and angles of a triangle
Circumference and area of circle CA-11. Regular polygons
SA-12. Circumference, area of a circle, area of a circle
KA-3. Circumference and area of a circle
movements . Movement concept
SA-14. Parallel transfer and rotation of KA-4. Movement KA-5. Annual test
Lesson-test on geometry in 9th grade “Coordinate method”
Lesson test on geometry in 9th grade
"Coordinate method"
Goals:
1. Test your knowledge of basic concepts, formulas on the topic, and the ability to apply them when solving standard problems.
2.Develop the ability to generalize your knowledge, choose methods of action, and the ability to exercise self-control;
3. Formation of a culture of mathematical speech, interest, perseverance, cooperation, collectivism.
The mark for the test on the topic is set based on the student’s participation in the work at stages 1 and 2 and at the individual level.
Stage "Theorists"
A theorem on the decomposition of a vector in two given non-collinear vectors. Decomposition of a vector into two coordinate vectors. The rule for finding the coordinates of the sum and difference of vectors. Rules for finding the coordinates of the product of a vector and a number. Formula for calculating the coordinates of a vector from the coordinates of its beginning and end. Formula for calculating the coordinates of the middle of a segment from the coordinates of its ends. Formula for calculating the length of a vector from its coordinates. Formula for calculating the distance between two points based on their coordinates. Equation of a circle of given radius with center at a given point. Equation of a circle of given radius with center at the origin. Equation of a straight line in a rectangular coordinate system.
“Practice” stage
Write down the vector decomposition of a vector Find the coordinates of a vector equal to the difference of vectors Find the coordinates of a vector equal to the sum of vectors Find the coordinates of vectors and, if, Find if Find the coordinates of the vector, if Find the coordinates of the point, if Find the coordinates of the midpoint of the segment, if Find the lengths of the vectors Find the length vector, if Find the length of the segment, if Find the length of the vector, if Find the coordinates of the point, if is the midpoint of the segment AB and Does the point lie on a circle? Write the equation of a circle if the center is , and the radius is 3. Write the equation of a straight line parallel to the ordinate axis passing through the point. Write the equation of a straight line parallel to the x-axis passing through the point. Write the equation of a circle with a center at the origin and a radius of 10.
The “Experts” stage is individual.
Given points A(-1;4), B(3;1), C(3;4). Find the coordinates of vector AB and its length. Find x if the distance between points A(2;3) and B (x;1) is 2. Prove that ∆ABC is isosceles if A(0;1), B(1;-4), C(5; 2). Find the median AH ∆ ABC if A(0;1), B(1;-4), C(5;2). On the x-axis, find a point equidistant from points A(1;1) and B(3;5). Prove that the quadrilateral MNPQ is a parallelogram and find its diagonals if M(1;1) N(6;1) P(7;4) Q(2;4) Given a circle (x+5)2+ (y- 1)2=16. Which of the points A(-2;4), B(-5;-3) lie on the circle? Given a circle x2+ y2=25. A(3;4), B(4;-3) Prove that the segment AB is a chord of the given circle. Write the equation of a circle with center at point A(-1;2) and radius R=2. Write the equation of a circle with its center at the origin and passing through point B(-1;3). Given ∆ ABC. A(4;6), B(-4;0), C(-1;-4). Write the equation for the SM median. Find the coordinates of the points of intersection of the straight line 3x-4y +12=0 with the coordinate axes.