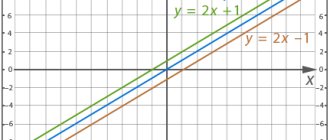
Линейное уравнение с двумя переменными
Вопросы занятия:
· повторить что такое линейное уравнение с одной переменной и сколько решений может иметь такое уравнение;
· ввести понятия «линейное уравнение с двумя переменными», «решение уравнения с двумя переменными», «равносильные уравнения».
Материал урока
Ранее мы с вами рассматривали линейное уравнение с одной переменной.
Вспомним, что:
Сегодня на уроке мы познакомимся с линейным уравнением, но уже с двумя неизвестными.
Давайте рассмотрим ситуацию
Полученное равенство содержит две переменные. А поэтому такие равенства называют уравнениями с двумя переменными
(или с двумя неизвестными).
Посмотрите на примеры уравнений с двумя переменными
Сформулируем определение:
Определение.
Линейным уравнением с двумя переменными
называется уравнение вида:
Вернёмся к задаче
То есть пара значений переменных (x
= 60
,
y= 110
) является решением этого уравнения. Отметим, что эти корни были найдены методом подбора, причём это не единственная пара чисел, удовлетворяющих нашему уравнению.
Определение.
Решением уравнения с двумя переменными
называется пара значений переменных, которая обращает это уравнение в верное равенство.
Вспомним, что при изучении уравнений с одной переменной, мы говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.
Аналогично можем сказать, что уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными
.
Причем уравнения с двумя переменными, не имеющие решений, также являются равносильными
.
Равносильные уравнения обладают следующими свойствами:
Свойство 1.
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнения, равносильное данному;
Свойство 2.
Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Снова вернёмся к нашему уравнению
Но здесь важно знать, значение какой из переменных стоит на первом месте, а какой – на втором. Так в нашем случае сначала записано значение переменной x
, а затем переменной
y
.
При этом пара чисел (150; — 25)
являясь решением уравнения, не удовлетворяет условию задачи, так как скорость автомобиля не может быть отрицательной.
И давайте рассмотрим ещё одну задачу.
Пример.
Решение уравнений в целых числах, то есть когда надо найти только целые значения переменных, подробно рассматривал древнегреческий математик Диофант.
Поэтому уравнения с несколькими переменными, которые надо решить в целых числах, называют диофантовыми уравнениями
. То есть уравнение, составленное в предыдущей задаче, является диофантовым, так как для него мы отыскивали только натуральные решения.
И давайте рассмотрим примеры.
Пример.
И ещё пример.
Пример.
Итоги урока
Итак, на этом уроке мы рассмотрели линейное уравнение с двумя переменными и один из способов решения таких уравнений.
Алгебра. Урок 4. Уравнения, системы уравнений
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Линейные уравнения
Примеры Особые случаи
- Квадратные уравнения
Примеры
- Разложение квадратного трехчлена на множители
Примеры
- Дробно рациональные уравнения
Примеры
- Системы уравнений
Метод подстановки Метод сложения
- Примеры решений заданий из ОГЭ
Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры линейных уравнений:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Для того, чтобы решить линейное уравнение, необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .
Примеры решения линейных уравнений:
- 2 x + 1 = 2 ( x − 3 ) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
2 x − 4 x = 2 − 1
− 2 x = 1
Теперь поделим левую и правую часть на число ( -2 ) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Ответ: x = − 0,5
- x 2 − 1 = 0
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
- x ( x + 3 ) − 8 = x − 1
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным уравнением.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
Примеры:
- 2 x − 4 = 2 ( x − 2 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 4
2 x − 2 x = − 4 + 4
0 = 0
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.
Ответ: x ∈ ( − ∞ ; + ∞ )
- 2 x − 4 = 2 ( x − 8 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
0 = − 12
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.
Ответ: x ∈ ∅
Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
- Выписать, чему равны в числах коэффициенты: a = … b = … c = …
- Вычислить дискриминант по формуле: D = b 2 − 4 a c
- Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
- Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
- Если D < 0, решений нет: x ∈ ∅
Примеры решения квадратного уравнения:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – будет два различных корня:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Ответ: x 1 = − 1, x 2 = 7
- − x 2 + 4 x − 4 = 0
a = − 1, b = 4, c = − 4
D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – будет один корень:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
Ответ: x = 2
- 2 x 2 − 7 x + 10 = 0
a = 2, b = − 7, c = 10
D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D < 0 – решений нет.
Ответ: x ∈ ∅
Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
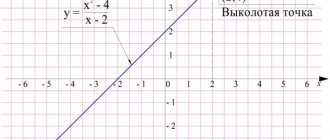
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 \ 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
- Выписать ОДЗ:
g ( x ) ≠ 0
2 − x ≠ 0
− x ≠ − 2
x ≠ 2
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
[ x 1 = 2 x 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
[ x 1 = 2 x 2 = − 3
ОДЗ: x ≠ 2
Значит, в ответ идет только один корень, x = − 3.
Ответ: x = − 3.
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
{ x + 2 y = 8 3 x − y = − 4
Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Пример:
Решить систему уравнений методом подстановки
{ x + 2 y = 8 3 x − y = − 4
Решение:
- Выразить из любого уравнения одну переменную через другую.
{ x = 8 − 2 y 3 x − y = − 4
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
{ x = 8 − 2 y 3 x − y = − 4
{ x = 8 − 2 y 3 ( 8 − 2 y ) − y = − 4
- Решить уравнение с одной неизвестной.
3 ( 8 − 2 y ) − y = − 4
24 − 6 y − y = − 4
− 7 y = − 4 − 24
− 7 y = − 28
y = − 28 − 7 = 28 7 = 4
y = 4
- Найти оставшуюся неизвестную.
y = 4
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Ответ:
- x = 0, y = 4
- { x = 0 y = 4
- ( 0 ; 4 )
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
если
{ a = b c = d
то
( a + c ) = ( b + d )
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Пример:
Решить систему уравнений методом сложения
{ x + 2 y = 8 3 x − y = − 4
Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .
{ x + 2 y = 8 | ⋅ ( − 3 ) 3 x − y = − 4
{ ( − 3 ) ⋅ ( x + 2 y ) = ( − 3 ) ⋅ 8 3 x − y = − 4
{ − 3 x − 6 y = − 24 3 x − y = − 4
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
{ − 3 x − 6 y = − 24 3 x − y = − 4 ⊕
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
− 7 y = − 28
y = − 28 − 7 = 28 7 = 4
Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.
x + 2 y = 8
x + 2 ⋅ 4 = 8
x + 8 = 8
x = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Ответ:
- x = 0, y = 4
- { x = 0 y = 4
- ( 0 ; 4 )
Способ подстановки
Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Пример 1
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {3x-y=-9} \end{array} \right.\] Выразим из второго уравнения $y$ через $x$:
\[y=3x+9\]
Подставим в первое уравнение, найдем $x$:
\[2x+9x+27=5\] \[11x=-22\] \[x=-2\]
Найдем $y$:
\[y=-6+9=3\]
Ответ: $(-2,\ 3)$
Готовые работы на аналогичную тему
- Курсовая работа Системы уравнений с двумя переменными, способы решения 470 руб.
- Реферат Системы уравнений с двумя переменными, способы решения 270 руб.
- Контрольная работа Системы уравнений с двумя переменными, способы решения 190 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость