Практическая работа по математике на тему "Многогранники и их поверхности"

Практическая работа по математике на тему «Многогранники и их поверхности»

Раздел 10.Многогранники

Тема.Многогранники и их поверхности.

Учебная цель:

Знать формулы вычисления площади боковой и полной поверхности призмы, пирамиды, параллелепипеда и уметь применять их к решению задач.

Учебные задачи:

обучающие:

— обобщить знания о многогранниках и их элементах;

— повторить формулы для вычисления площадей поверхности прямоугольного параллелепипеда, призмы, пирамиды;

— закрепить практические навыки вычисления площадей поверхностей многогранников;

— расширить знания в области математики, показать её прикладной характер;

развивающие:

— развитие познавательного интереса, логического мышления, пространственного воображения и исследовательских способностей;

— развитие вычислительных навыков, ключевых компетенций, умений сравнивать, анализировать, аргументировать сделанный выбор;

воспитательные:

— воспитание ответственности, умения работать в коллективе, принимать самостоятельные решения;

— показать значимость знаний, возможность их применения на практике.

Обеспеченность занятия:

1.Учебно-методическая литература:

Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014.

2.Рабочая тетрадь: в клетку

3.Раздаточные материалы (карточки-задания, по количеству обучающихся).

4.Калькулятор: простой.

5.Ручка.

6.Карандаш простой.

7.компьютер,

8.мультимедийный проектор,

9.экран.

Краткие теоретические и учебно-методические

Практическая работа «Пирамида. Призма»

Практическая работа

По теме: «Пирамида»

Цели:

закрепление понятий: пирамида, площадь боковой и полной поверхности пирамиды; воспитание познавательной активности , показать возможность применения пирамиды в различных областях.

Методические указания

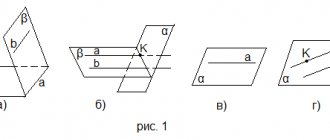
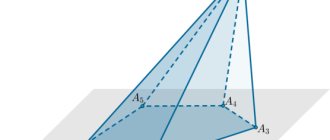
Пирами́да

— многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.

наклонная прямая

Элементы пирамиды.

– высота пирамиды

ДВ, ДС, ДА

— боковые ребра — общие стороны боковых граней;

ДВА, ДАС, ДВС

— боковые грани — треугольники, сходящиеся в вершине пирамиды

ДК, ДL
— апофема
— высота боковой грани правильной пирамиды, проведенная из ее вершины [ℓ];
ДN
— высота пирамиды.

Пирамида называется правильной

, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

боковые ребра правильной пирамиды равны; в правильной пирамиде все боковые грани — равные равнобедренные треугольники; в любую правильную пирамиду можно как вписать, так и описать около неё сферу;

Прямоугольная пирамида

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Усечённая пирамида

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Боковая поверхность

— это сумма площадей боковых граней.

Для нахождения боковой поверхности в правильной пирамиде можно использовать формулу:

Sб.п.= 1/2•Р•ℓ, где Р – периметр основания.

Полная поверхность

— это сумма площади боковой поверхности и площади основания.

Для нахождения полной поверхности в правильной пирамиде можно использовать формулу:

Sп.п. = 1/2•Р•ℓ+Sосн.

Вариант 1

. Сколько ребер у шестиугольной пирамиды: а)6; б)12; в)18; г)24;

. Какое наименьшее число граней может иметь пирамида: а)5; б)4 в)10; г)6

. Подтвердите или опровергните следующие утверждения: Да ^ нет

а) Многогранник, составленный из n-треугольников, называется пирамидой; б) Пирамида называется правильной, если ее основание – правильный многоугольник; в) Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой;

.
Задача.
Крыша башни имеет вид правильной четырехугольной пирамиды, у которой сторона основания равна 12 м, а высота 18 м. Сколько понадобится плиток на покрытие этой крыши, если каждая плитка имеет вид прямоугольника со сторонами 22 см и 18 см.

Вариант 2

. Сколько граней у шестиугольной пирамиды: а)6; б)7; в)8; г)10;

. Какое наименьшее число ребер может иметь пирамида: а)6; б)5; в)4; г)7;
3
Подтвердите или опровергните следующие утверждения: Да ^ нет а) Высота пирамиды называется высотой грани; б) Площадь боковой поверхности пирамиды равна произведению периметра основания на высоту; в) Пирамида называется правильной, если ее основание – правильный многоугольник;

.
Задачи
. Одно из самых грандиозных сооружений древности – пирамида Хеопса – имеет форму правильной четырехугольной пирамиды с высотой 150 м и боковым ребром 220 м. Найдите площадь боковой поверхности

Вариант 3

. Сколько ребер у четырехугольной пирамиды: а)6; б)12; в) 8

. Какое наименьшее число граней может иметь пирамида: а)5; б)4 в)10; г)6

.Подтвердите или опровергните следующие утверждения: Да ^ нет а)Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию? б)Высота пирамиды, это перпендикуляр, проведённый из вершины к основанию. в)Общая точка боковых граней пирамиды называется вершиной

.
Задача
. Крыша имеет форму пирамиды с квадратным основанием 4,5 м х 4,5 м и высотой 4 м. Сколько листов железа размером 70 см х 140 см нужно для покрытия крыши, если на отходы нужно добавить 10% площади крыши?

Практическая работа

По теме: « Призма»

Цели:

закрепление понятий: прямоугольный параллелепипед, линейные размеры, диагональ, площадь боковой и полной поверхности призмы; содействовать воспитанию интереса к математике и ее приложениям.

Методические указания

Призма

— многогранник, две грани которого являются многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.

Виды призм.

Призма, основанием которой является параллелограмм, называется параллелепипедом
.
Прямая призма
— это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются
наклонными
.
Правильная призма
— это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.

прямая призма наклонная призма

Свойства призмы:

Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.

Площадь боковой поверхности прямой призмы

:
Sб.п.=P•H
где P — периметр основания призмы (сумма всех сторон основания), H — высота призмы.

Площадь полной поверхности призмы

равна сумме площади её боковой поверхности и удвоенной площади основания:
Sп.п.=P•H+2•Sосн
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его линейных размеров: d2
=a2+b2+c2
Задания для самостоятельной работы:

Вариант 1

. Сколько ребер у шестиугольной призмы?

Ответ: а)18, б)24, в)12.

.Выберите верное утверждение.

а) призма называется правильной, если ее основания — правильные многоугольники;

б) у треугольной призмы две диагонали;

в) высота призмы равна ее боковому ребру;

3.Задача

. Найдите длину диагонали прямоугольного параллелепипеда, если его измерения равны 2м, 3м, 5м.

.
Задача.
Коллекционер заказал аквариум, имеющий форму правильной четырехугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 70 см, а высота 60 см?

Вариант 2

.Сколько граней у шестиугольной призмы?

Ответ: а)6, б)8, в)10

. Выберите верное утверждение.

а) площадь полной поверхности призмы называется сумма площадей ее боковых граней и основания;

б) у треугольной призмы нет диагоналей;

в) высота прямой призмы равна ее боковому ребру;

.
Задача.
Найдите длину диагонали прямоугольного параллелепипеда, если его измерения равны 3см, 4см, 5см.

4. Задача

Необходимо изготовить короб с крышкой для хранения картофеля в форме прямой призмы высотой 0,7 м. В основании призмы лежит прямоугольник со сторонами 0,4 м и 0,6 м. Сколько фанеры понадобиться для изготовления короба?

Вариант 3

.Сколько граней у четырехугольной призмы?

Ответ: а)6, б)8, в)10

. Выберите верное утверждение.

а) У n – угольной призмы 2 n ребер;

б) площадь полной поверхности призмы называется сумма площадей ее боковых граней;

в) у треугольной призмы три диагонали;

.
Задача.
Сколько необходимо купить листов 8 – волнового шифера размером 1750*1130 мм на покрытие крыши здания длиной 10 м. Фронтон имеет форму равнобедренного прямоугольного треугольника с гипотенузой 10 м и катетом 7 м.

.
Задача.
Нужно оклеить обоими типа « рогожка», комнату, длина которой 6м, ширина 4м, высота 3м, площадь окон и дверей составляет 1/5 всей площади стен. Сколько нужно рулонов обоев для оклейки комнаты, если длина рулона 12 м, а ширина 50 см?

Загадки пирамид

Во-первых, это загадки, связанные с процессом и технологией строительства пирамид. В ходе экспедиций и археологических исследований не было найдено ни описаний, ни рисунков, связанных со строительством пирамид. Предположения о ходе и технологиях постройки пирамид были сделаны на основании существующих знаний о строительных технологиях древних цивилизаций.

Были предположены: примерное количество рабочих – сотни тысяч человек; способы транспортировки каменных блоков – по Нилу в период разлива, когда площадь водной поверхности значительно увеличивалась и удлинялась, позволяя осуществить перевозку на максимальное расстояние; а также возможные типы инструментов, устройств и механизмов. Однако, во всех этих вопросах очень много натяжек и ничем не подтверждаемых предположений: например, известно, что египтяне не знали железа, бронзы, сплавов, использовали только каменные и медные орудия, примитивные отвесы, уровни, треугольники и другие измерительные приборы.

Но при этом две самые сложные проблемы – идеальное выравнивание основания под здание и соблюдение угла наклона краеугольных камней так, чтобы края слились на большой высоте, — выполнены на самом высоком и точном математическом уровне. Осуществить эту задачу, имея под руками столь несовершенный ассортимент приборов, просто невозможно. Таким же невозможным выглядит и транспортировка и, в еще большей степени, подъем и установка каменных блоков с ювелирной точностью, при том, что строители не располагали ни кранами, ни другими современными строительными механизмами.

Во-вторых, общепризнанная точка зрения на предназначение пирамид – то, что они являются просто грандиозными гробницами для фараонов, не объясняет того, что ни в одной пирамиде не было найдено тело фараона, а также тот факт, что помимо так называемой погребальной камеры в пирамидах, в результате современных исследований, найдено еще большое число разных пустых, непонятного предназначения помещений, коридоров, заканчивающихся тупиками, подземных камер и т.п.

И, в третьих, существуют особенности пирамид, выходящие далеко за рамки уровня развития цивилизации на тот момент и теории о погребальном предназначении этих сооружений.

Математические: в геометрическом строении пирамид заложены принцип «золотого сечения», число «пи» и разные другие особенности из области тригонометрии и высшей математики.

Астрономические: высокоточная астрономическая ориентация пирамид по сторонам света; в них имеются ходы, ориентированные строго на определенные звезды.

Геологические: кроме местного материала в строительстве использовались гранит (предположительно привезенный из местности, находящейся в 900 км выше по течению Нила) и базальт неизвестного происхождения.

Технологические: при строительстве многократно использовались плиты весом более 200 тонн, а также миллионы известняковых блоков весом 2,5 тонны; применялись методы шлифовки неизвестными инструментами, точность и чистота просверленных отверстий не соответствует даже современным строительным сверлам и бурам и т.п. (4)

Кроссворд с вопросами и ответами по геометрии для 7 класса: Многоугольники и многогранники

Кроссворд и игра для 7 класса по теме «Многоугольники и многогранники»
Автор: Пестова Юлия Рямильевна, МБОУ «СОШ №76», г. Ульяновск Описание материала: Предлагаю вам материал, который может быть использован для закрепления знаний учащихся 7 класса по теме «Многоугольники и многогранники». В состав входят кроссворд и игра «Больше и быстрее», которые я уверена заинтересуют ребят и помогут сплотить коллективный дух.
Кроссворд и игра «Больше и быстрее» по теме «Многоугольники и многогранники»
Цель: обобщение и систематизация знаний по теме «Многоугольники и многогранники» Задачи: — сбособствовать развитию сообразительности, логического мышления, математической эрудиции учащихся — воспитывать познавательный интерес у учащихся — уметь работать в парах и коллективно
Кроссворд

Вопросы: 1. Если фигуры составлены из одинаковых частей, то они называются … ? 2. Параллелограмма, все стороны которого равны? 3. Если провести две пары параллельных прямых, то при их пересечении образуется четырехугольник, противоположные стороны которого параллельны. Как называется этот четырехугольник? 4. Угол, величина которого больше 90 градусов, но меньше 180 градусов? 5. Плоская фигура, образованная замкнутым рядом прямолинейных отрезков? 6. Сторона многогранника? 7. Многоугольник, у которого равны все стороны и все углы, называется … ? 8. Отрезок, соединяющий 2 вершины, не лежащие на одной грани? 9. … симметрии параллелограмма – точка пересечения его диагоналей? 10. Тело, граница которого состоит из кусков плоскостей (многоугольников)? 11. Из Древней Греции пришло к нам слово «ромб», означающий « … », силуэт которого действительно имеет форму ромба. Ответы: 1. равносоставленные 2. ромб 3. параллелограмм 4. тупой 5. многоугольник 6. ребро 7. правильный 8. диагональ 9. центр 10. многогранник 11. волчок Главное слово: треугольник
Игра «Больше и быстрее»
Задача учащихся: класс разделен на 2 команды. Каждая команда должна попытаться как можно быстрее добраться от С до Ф (ходить можно только вниз, влево, вправо) и иметь не меньше 30 баллов в общей сумме, в противном случае победа переходит к другой команде. Если команда не может ответить на вопрос, то он переходит к другой команде. Если эта команда на него отвечает, то она остается на своем же месте, но плюсуя к своей сумме очки, в которые оценивался вопрос.

Вопросы: в 5 баллов: 1. Слово «параллелограмм» происходит от греческого « … » (изображенный параллельными) 2. Каким свойством обладают диагонали параллелограмма (точкой пересечения делятся пополам) 3. Чем прямоугольник отличается от квадрата (у него стороны попарно равны, а у квадрата все стороны равны) 4. Назовите 5 правильных многогранников (тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр) 5. Составьте формулу для вычисления площади прямоугольного треугольника с катетами а и b (S = 1/2ab) в 4 балла: 1. Что такое центр симметрии параллелограмма? (точка пересечения его диагоналей) 2. Назовите 3 вида каких-нибудь правильных многоугольников (равносторонний треугольник, квадрат, шестиугольник и так далее) 3. Каким важным свойством обладают все вершины правильного многоугольника (лежат на одной окружности) 4. Какой многоугольник называется правильным? (все стороны и углы которого равны) 5. Это слово с греческого означает «отпиленный кусок» (призма) в 3 балла: 1. Если шестиугольник правильный, то каждый его угол равен … (120 градусов) 2. Каким свойством обладают диагонали ромба (они перпендикулярны между собой) 3. Какая фигура называется правильным многогранником (все грани которой равны) 4. Призма, все грани которой прямоугольники (параллелепипед) 5. Среди граней призмы различают … (боковые грани и основания) в 2 балла: 1. Основное свойство равнобедренного треугольника (углы при основании равны) 2. Параллелограмм, все стороны которого равны (ромб) 3. Сколько осей симметрии у правильного треугольника (3) 4. Если фигуры составлены из одинаковых частей, то они … (равносоставлены) 5. Две фигуры, имеющие одинаковые площади, называют … (равновеликими) в 1 балл: 1. Четырехугольник с равными сторонами и углами (квадрат) 2. Сумма углов треугольника равна … (180 градусов) 3. Чему равна величина угла равностороннего треугольника (60 градусов)

Практическая работа «Правильные многогранники»

Разработал: Рудакова Марина Александровна, преподаватель математики

Место работы: Байкаловский филиал ГАПОУ СО «Слободотуринский аграрно-экономический техникум»

Практическая работа «Правильные многогранники»

Цель:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Задания:

Задание №1.

Выполните кроссворд «Правильные многогранники»


1
2	3
4
5
6
7	8
9	10
11
12
		13

По горизонтали:

Правильный шестигранник.
4.
Плоские многоугольники, из которых состоит поверхность многогранника.
6.
Правильный двадцатигранник.
7.
Правильный двенадцатигранник.
9.
Из какого многоугольника состоит куб.
11.
Выпуклая точка, соединяющая многоугольники многогранника.
12.
Древнегреческий философ, подробно описавший правильные многогранники.
13.
Правильный восьмигранник.

По вертикали:

Треугольная пирамида.
3.
Сторона грани многогранника.
5.
Тело, поверхность которого состоит из конечного числа плоских многоугольников.
8.
Автор теоремы (формулы)
В+Г=Р+2,
показывающей зависимость между вершинами, гранями и рёбрами выпуклого многогранника.
10.
Из какого многоугольника состоит тетраэдр, октаэдр.

2 задание.

Провести исследование Платоновых тел:

1)Посчитать количество вершин, ребер и граней.

2)Найти между ними зависимость используя теорему Эйлера В-Р+Г=2.

3)Сколько у нас получилось Платоновых тел для которых выполняется теорема Эйлера?

4)Что представляют собой грани исследуемого Платонового тела?

1) тетраэдр:  —  +  = , состоит из _________________________

2) гексаэдр:  —  +  = , состоит из _________________________

3) октаэдр:  —  +  = , состоит из _________________________

4) икосаэдр:  —  +  = , состоит из _________________________

5) додекаэдр:  —  +  = , состоит из _________________________

3 задание.

1 уровень

Нужно рассчитать количество краски на потолок в форме квадрата со стороной 6м.

Решение:

1)Для потолка площадь будет равна: длина комнаты умножить на ширину.

_______________________________________

2)Если на этикетке банки указан расход краски на однослойное покрытие 100 г/м2, то на 36 м2 расход будет равен

_______________________________________

3)Если краска расфасована в банки по 2,5 кг, то сколько необходимо купить?

_______________________________________

4)Если краска в продаже имеется только в банках по 1 кг, то сколько придется покупать банок?

_______________________________________

Практическое занятие по теме»Элементы пирамиды» методическая разработка на тему