Geometry tests for grade 10 (page 1)

Tests on geometry in 10th grade

TOPICS OF CONTROL WORKS ON GEOMETRY IN 10TH GRADE

Diagnostic test work

Test work on the topic “Axioms of stereometry. The relative position of two lines in space"

Test on the topic “Parallelism of lines and planes in space”

Semester test

Test on the topic “Perpendicularity of a line and a plane. Perpendicular and oblique"

Test on the topic “Theorem of three perpendiculars. Perpendicularity of planes"

Test on the topic “Coordinates in space”

Test on the topic “Vectors in space”

Software on the topic “Coordinates and vectors in space”

Final test"

Diagnostic test work

Option-1

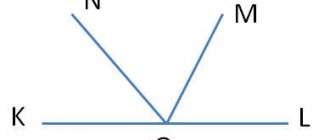
From point M to straight line A
a perpendicular MV and inclined MA and MS are drawn.
Find the length of the perpendicular if the inclined slopes MA = 41 cm,
MB = 50
cm,
and their projections onto this line are in the ratio 3:10.

In a right triangle, the median and altitude are drawn from the vertex of the right angle to the hypotenuse, the distance between the bases of which is 14 cm.
Find the perimeter of a triangle if its hypotenuse is 100
cm.
Read also: Flowers from foamiran, presentation for the lesson (preparatory group)

The sides of a parallelogram are 6 cm
and 7
cm,
and the sum of its diagonals is 18
cm
. Calculate the diagonals of the parallelogram.

Diagnostic test work

Option-2

From point M to straight line A
a perpendicular MV and inclined MA and MS are drawn.
Find the length of the perpendicular if the lengths of the inclined ones are in the ratio 10:17, and their projections onto a given line are 12 cm
and 30
cm
.

In a triangle, the side is 6 cm
, one of the angles adjacent to this side is equal to , the side opposite this angle is equal to 28
cm
. Find the area of the triangle.

The diagonals of a parallelogram are 12 cm
and 14
cm
, and the difference between the sides is 4
cm
. Calculate the perimeter of the parallelogram.

Thematic test

on the topic “Parallelism of lines and planes in space”

Option-1

Draw a cube ABCDABCD. Points K, L, M are the midpoints of edges AB, AD, AA, respectively.

a) Write down the edges of the cube parallel to faces ABCD.

b) What is the relative position of the straight line KL and the plane BDC?

c) What is the relative position of the KLM and BDA planes?

Side AB of triangle ABC lies in the plane, but vertex C does not lie in this plane. Points M and N are the midpoints of sides AC and BC, respectively. Prove that the line MN is parallel to the plane.

Segment AB does not intersect the plane, C is the middle of segment AB. Parallel lines are drawn through points A, B, C, intersecting the plane at points A, B, C, respectively. Find AA if BB = 4 cm, CC = 3 cm.

Thematic test

on the topic “Parallelism of lines and planes in space”

Option-2

Draw a cube ABCDABCD. Points K, L, M are the midpoints of edges AB, AD, AA, respectively.

a) Write down the faces of the cube parallel to edge AA.

b) What is the relative position of straight line ML and plane ADC?

c) What is the relative position of the KLM and BDC planes?

The base AD of the trapezoid ABCD lies in the plane, and points B and C do not belong to this plane. Prove that line BC is parallel

plane

The plane intersects sides AB and AC of triangle ABC at points B and C, respectively, BC //. Find AC if AC = 2 cm,

Sun : Sun=2

Semester test

Option-1

The straight line has one common point with the plane of the triangle. Will this line belong to the plane of the triangle?

Planes and parallel. Side AB of triangle ABC belongs to the plane, the plane intersects side AC at point A, and side BC at point B. In this case, AB:AB = 5:4. Segment AA = 18 cm. Find AC.

Planes and parallel. Line AB lies in the plane, and line CD lies in the plane, while AB is not parallel to CD. Will lines AC and BD be parallel?

Semester test

Option-2

A straight line intersects adjacent sides of a rhombus. Will this line belong to the plane of the rhombus?

Segment AB does not intersect the plane. Parallel lines are drawn through the ends of the segment and its middle, intersecting the plane at points A, M, B. Find the length of the segment AA if MM = 5 cm and BB = 7 cm.

Outside the plane of triangle ABC lies point S. On the segments

AS, BS, CS are marked respectively points M, N, K so that

AM:MS=BN:NS=CK:KS=2:1. Prove that the planes MNK and

ABC are parallel.

Thematic test

on the topic “Perpendicularity of a line and a plane. Perpendicular and oblique"

Option-1

Draw a cube ABCDABCD. Using a picture of a cube, write down the edges of the cube that are perpendicular to and intersecting edge AA.
An inclined AB is drawn from point A to the plane. Find the length of the projection of this inclined plane if AB = 26 cm and point A is 10 cm away from the plane.
From point A, taken outside the plane, two inclined ones are drawn to it, the lengths of which are 10 and 17 cm. The difference in the projections of these inclined ones onto the plane is 9 cm. Find the projections of the inclined ones.
The distance from point M to all vertices of the square is

10 cm. Find the distance from point M to the plane

square if the diagonal of the square is 12 cm.

Thematic test

on the topic “Perpendicularity of a line and a plane.

Perpendicular and oblique"

Option-2

Draw a rectangular parallelepiped ABCDABCD. Using its image, write down the faces of the parallelepiped perpendicular to edge AA.
An inclined MN is drawn from point M to the plane. Find the length of the inclined line if the length of its projection onto the plane is 8 cm, and point M is 6 cm away from the plane.
From point A, taken outside the plane, two inclined ones are drawn to it. Find the lengths of the inclined ones if one of them is on

13 cm is larger than the other, and the projections are inclined onto the plane

equal to 6 and 20 cm.

The distances from point S to all vertices of a regular triangle are equal to 5 cm, and to the plane of the triangle -

3 cm. Find the height of the triangle.

Thematic test

on the topic “Perpendicularity of a line and a plane. Perpendicular and oblique"

Option-3

Draw a cube ABCDABCD. Using the image of a cube, write down the edges of the cube perpendicular to face ABCD
An inclined AB is drawn from point A to the plane. Find the distance from point A to the plane if AB = 17 cm, and the length of the projection of AB onto the plane is 8 cm.
From point A, taken outside the plane, two inclined ones are drawn to it, the projection lengths of which are 2 and 14 cm, and the inclined ones are in the ratio 1:2. Find the lengths of the inclined ones.
The distances from point M to all vertices of the square are equal in

13 cm, and to the plane of the square - 12 cm. Find the diagonal of the square.

Thematic test

on the topic “Perpendicularity of a line and a plane.

Perpendicular and oblique"

Option-4

Draw a rectangular parallelepiped ABCDABCD. Using its image, write down the edges of the parallelepiped that are perpendicular to edge DC and intersecting it.
An inclined MN is drawn from point M to the plane. Find the length of the projection of this inclined plane onto the plane if

MN = 20 cm, and point M is 12 cm away from the plane.

From point A, taken outside the plane, two inclined ones are drawn to it, the projections of which are equal to 8 and 20 cm. Find the lengths of the inclined ones if it is known that their difference is 8 cm.
The distance from point S to each vertex of a regular triangle is 10 cm. Find the distance from point S to the plane of the triangle if the median of the triangle is 9 cm.

Thematic test

on the topic “ Theorem of three perpendiculars.

Perpendicularity of planes»

Option 1

A straight line MC is drawn through vertex C of square ABCD, which is perpendicular to the plane of the square.

1) Prove that straight lines BD m MO are perpendicular, where

O is the point of intersection of the diagonals.

2) Calculate the distance from point M to straight line ВD, if

MS = 1 cm, CD = 4 cm.

The ends of a segment whose length is equal to cm belong to two mutually perpendicular planes. The distances from the ends of this segment to the line of intersection of the planes are 5 cm and 8 cm. Find the distance between the bases of the perpendiculars drawn from the ends of the segment to the line of intersection of the planes.
A perpendicular DE is drawn through vertex D of rectangle ABCD to its plane. Point E is 10 cm away from side AB, and 17 cm from side BC. Find the length of diagonal ВD if ЕD = 8 cm.

Thematic test

on the topic “ Theorem of three perpendiculars.

Perpendicularity of planes»

Option-2

Through vertex A of equilateral triangle ABC, a straight line DA is drawn, which is perpendicular to the plane of the triangle, M is the middle of side BC.

1) Prove that lines BC and MD are perpendicular.

2) Calculate the distance from point D to straight line BC, if

AD = 4 cm, AB = 6 cm.

The ends of a segment whose length is equal to cm belong to two mutually perpendicular planes. The distances from the ends of this segment to the line of intersection of the planes are 6 cm and 7 cm. Find the distance between the bases of the perpendiculars drawn from the ends of the segment to the line of intersection of the planes.
A perpendicular CF is drawn through vertex C of the rhombus ABCD to its plane. Point F is 25 cm away from diagonal ВD. Find the distance from point F to the plane of the rhombus if

ВD = 20 cm, АВ = cm.

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option 1.

Given points A(1;0;-2), B(-2;1;3) and vector (1;0;-2).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of the sum of vectors and .

Find the length of the vector 2+3 if (3;1;0), (0;1;-1).
Find the cosine C of triangle ABC if A(0;1;-1),

B(1;-1;2), C(3;1;0).

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option – 2.

. Given points A(3;2;1), B(1;2;3) and vector (1;1;1).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of the difference between vectors and .

. Find the length of the vector -3+2 if (3;-2;-1), (1;2;-4).

Find the cosine A of triangle ABC if A(0;1;-1),

B(1;-1;2), C(3;1;0).

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option – 3.

Given points C(1;0;1), D(1;1;2) and vector (1;2;3).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of vector 2.

Find the length of the vector 2+3 if (1;1;-1), (2;0;0).

. Find the value B of triangle ABC if A(2;2;-4),

B(2;-1;-1), C(3;-1;-2).

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option – 4.

. Given points M(1;0;2), K(1;1;2) and vector (1;-1;0).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of vector 3.

. Find the length of the vector -2+3 if (2;-1;3), (-1;2;5).

. Find the value A of triangle ABC if A(2;-2;-3)

B(4;-2;-1), C(2;2;1).

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option – 5.

. Given points K(1;0;-2), P(-2;1;3) and vector (1;0;-2).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of the difference between vectors and .

. Find the length of the vector -2 + 3 if (3;1;0), (0;1;-1;).

. Find the cosine C of triangle ABC if A(0;1;-1),

B(1;-1;2), C(3;1;0).

TEST ON THE TOPIC

"VECTORS IN SPACE"

Option – 6.

. Given points M(1;2;3), N(3;2;1) and vector (2;3;1).Find:

a) vector coordinates;

b) the absolute value of the vector;

c) coordinates of the sum of vectors and .

Find the length of the vector 3-2 if (2;0;-3), (1;-2;-1).

Find the cosine A of triangle ABC if A(0;1;-1),

B(1;-1;2), C(3;1;0).

Software on the topic

"Coordinates and vectors in space."

Option 1

Given three vertices A(1;-2;3), B(2;3;-5), D(-4;5;1) of parallelogram ABCD. Find the coordinates of its fourth vertex C.
Find on axis at
a point equidistant from points A(-3;7;4) and B(2;-5;1).
Given points M(3;-2; 2), N(2;-1;0), K(-1;-5;4) and P(0;-4;4). Find the angle between the vectors and .
Given vectors and such that =4, =
3, and the angle between the vectors and is equal to 120. Find 3+2.

Software on the topic

"Coordinates and vectors in space."

Option –2

. Given three vertices A(2;-8;9), B(-1;3;4), C(-4;6;3)

parallelogram ABCD. Find the coordinates of his fourth

vertices D.

Find a point on
the x-
equidistant from the points M(-2;6;3) and

P(4;-3;5).

Given points A(1; 3; 3), B(1;0;2), C(-1;-1;3) and D(-1;0;3).

Find the angle between the vectors and .

Given vectors and such that =3, =
2, and the angle between the vectors and is equal to 60. Find 2-3.

Final test

in geometry in 10th grade.

Option 1.

In triangle ABC C=90, AC=9 cm, BC=12 cm,

M-mid VA. Straight line KS is perpendicular to plane ABC, KS = 18 cm. Find KM.

A perpendicular SC is drawn from the vertex of right angle C of triangle ABC to its plane. The distance from point K to line AB is 13 cm. Find the distance from point K to the plane of the triangle if its legs are 15 cm and 20 cm.

1) Find the coordinates of the point M - the middle of the segment AB, if A(-2;3;4), B(6;1;-2). 2) Find the length of the vector.

3) Find the scalar product of vectors and .

Final test

in geometry in 10th grade.

Option – 2.

From vertex A of regular triangle ABC, a perpendicular AK is drawn to the plane of the triangle. Find the distance from point K to the vertices of the triangle, if BC = cm, KVA = 30.

A perpendicular SC is drawn from the vertex of angle C of triangle ABC to its plane. The distance from point K to straight line AB is 26 cm. Find the distance from point K to the plane of the triangle if AC = 30 cm, AB = 28 cm,

BC=26 cm.

1) Find the coordinates of the point M - the middle of the segment AB, if A(-3;0;4), B(3;5;-2). 2) Find the length of the vector.

3) Find the scalar product of vectors and.

G10(I)-1. Parallelism of straight lines, line and plane

Geometry. 10 . Chapter I. _ Test 1 .

Option 1.

1. Choose the correct statement.

1) Two lines in space are called parallel if they do not intersect.

2) If one of two parallel lines is parallel to a given plane, then the other line is either also parallel to a given plane or lies in this plane.

3) If a line is parallel to some line lying in a plane, then it is parallel to this plane.

4) Through any point in space there passes a line parallel to a given line, and only one.

A ) 1; B ) 4; C ) 3; D ) 2.

2. Which of the drawings in Figure 1 can illustrate the following statement: if one of two parallel lines intersects a given plane, then the other line also intersects this plane?

A ) b); B ) a); C ) c); D ) g).

3. In Figure 2, points E, F, P and K are the midpoints of segments AC, AM, BM and BC. Find the perimeter of the quadrilateral EFPK,

if MC=21 cm, AB=13 cm.

A ) 8 cm; B ) 34 cm; C ) 17 cm; D ) 68 cm.

4. Side AC of triangle ABC lies in the α plane. МϵАВ, NϵBC, MN||α, with BM : AM=2 : 7, MN=6 cm. Make a drawing. Find AC.

A ) 18 cm; B ) 30 cm; C ) 27 cm; D ) 36 cm.

Option 2.

1. Choose the correct statement.

1) If a plane passes through a line parallel to another plane, then these planes will be parallel.

2) If two lines are parallel to a third line, then they are perpendicular.

3) If a line is parallel to some line lying in a plane, then it is parallel to this plane.

4) If one of two parallel lines intersects a given plane, then the other line also intersects this plane.

A ) 1; B ) 4; C ) 3; D ) 2.

2. Which of the drawings in Figure 1 can serve as an illustration of the following statement: through any point in space that does not lie on a given line, there passes a line parallel to the given one, and only one?

A ) b); B ) a); C ) c); D ) g).

3. In Figure 2, points F, P, Q and N are the midpoints of segments AB, AM, CM and BC. Find the perimeter of the quadrilateral FPQN if AC=17 cm, BM=25 cm.

A ) 32 cm; B ) 21 cm; C ) 42 cm; D ) 84 cm.

4. Plane α is parallel to side AC of triangle ABC and intersects sides AB and BC at points K and F, respectively, BF : FC = 5 : 6, AC = 22 cm. Make a drawing. Find KF.

A ) 15 cm; B ) 9 cm; C ) 10 cm; D ) 12 cm.

Option 3.

1. Choose the correct statements.

1) If a plane passes through a given line parallel to another plane and intersects this plane, then the line of intersection of the planes is parallel to the given line.

2) If parallel lines a and b lie in the α plane, then the line c intersecting the lines a and b lies in the α plane.

3) If the midline of a trapezoid lies in the α plane, then the straight lines containing its bases will intersect the α plane.

A ) 1); 2); 3); B ) 1); 3); C ) 1); 2); D ) 2); 3).

2. What drawing(s) in Figure 1 can illustrate the following statement.

There are three possible cases of relative position of a straight line and a plane: a) a straight line and a plane have only one common point; b) the straight line lies in the plane; c) a straight line and a plane do not have a single common point.

A) b); V); B ) a); b); G); C ) b); V); G); D ) a).

3. In Figure 2, points E, F, P and K are the midpoints of segments AC, AM, BM and BC. The perimeter of the quadrilateral EFPK is 32 cm, and the difference in the lengths of any of its adjacent sides is 2 cm. Find MC and AB (MC

A) MC=14 cm; AB=18 cm; B) MC=15 cm; AB=17 cm;

C) MC=12 cm; AB=20 cm; D) MC=10 cm; AB=22 cm.

4. Segment AB intersects plane α at point O. Point C is the middle of segment OB. Parallel lines drawn from points A, B and C to the plane α intersect it at points A1, B1 and C1, respectively. AA1=6 cm, A1O : OC1=1 : 3. Make a drawing. Find BB1.

A ) 18 cm; B ) 30 cm; C ) 32 cm; D ) 36 cm.

Option 4.

1. Choose the correct statements.

1) If a line that does not lie in a given plane is parallel to some line that lies in this plane, then it is parallel to the given plane.

2) There are three possible cases of relative position of a straight line and a plane: a) the straight line lies in the plane; b) a straight line and a plane intersect; c) the straight line and the plane are parallel.

3) If the sides MN and NP of the parallelogram MNPQ intersect the plane α, then the lines MQ and PQ will intersect this plane.

A ) 1); 2); 3); B ) 1); 3); C ) 1); 2); D ) 2); 3).

2. What drawing(s) in Figure 1 can illustrate the following statement.

If a plane passes through a given line parallel to another plane and intersects this plane, then the line of intersection of the planes is parallel to the given line.

A) b); V); B ) a); C ) a); b); D ) a); G).

3. In Figure 2, points F, P, Q and N are the midpoints of segments AB, AM, CM and BC. The perimeter of the quadrilateral FPQN is 38 cm, and the difference in the lengths of any of its adjacent sides is 3 cm. Find AC and BM (AC

A) AC=14 cm; BM=24 cm; B) AC=16 cm; BM=26 cm;

C) AC=16 cm; BM=19 cm; D) AC=16 cm; BM=22 cm.

4. Segment AB intersects plane α at point O. Point C is the middle of segment OB. Parallel lines drawn from points A, B and C to the plane α intersect it at points A1, B1 and C1, respectively, AO : OS = 5 : 3, BB1 = 24 cm. Make a drawing. Find AA1.

A ) 20 cm; B ) 24 cm; C ) 12 cm; D ) 10 cm.

Reference materials.

Two lines in space are called parallel if they lie in the same plane and do not intersect.

Through any point in space that does not lie on a given line, there passes a line parallel to the given one, and, moreover, only one.

If one of two parallel lines intersects a given plane, then the other line also intersects this plane.

If two lines are parallel to a third line, then they are parallel.

There are three possible cases of relative position of a straight line and a plane in space: a) the straight line lies in the plane; b) a straight line and a plane have only one common point, that is, they intersect; c) a straight line and a plane do not have a single common point.

A line and a plane are called parallel if they do not have common points.

If a line not lying in a given plane is parallel to some line lying in this plane, then it is parallel to the given plane.

If a plane passes through a given line parallel to another plane and intersects this plane, then the line of intersection of the planes is parallel to the given line.

If one of two parallel lines is parallel to a given plane, then the other line is either also parallel to the given plane or lies in this plane.

Tags: Geometry grade 10, parallelism of lines and planes, straight line and plane

Your comment Cancel reply

Practical lesson. Topic: Perpendicular and oblique.

Practical lesson

Topic:
Perpendicular and oblique .
Goals :

Educational:

continue to develop students’ ability to solve problems on the topic “Perpendicular and Oblique”.

Educational:

fostering independence and a creative approach to problem solving.

Developmental:

development of logical thinking, comparative analysis skills.

Equipment:

board, computer, projector, screen, individual task cards, notes on the board.

Using elements of pedagogical technologies:

1. cooperation;

2. health of savers (alternation of activities);

3. information and communication;

4. developing;

5. person-oriented.

Performance:

formation of competencies: value-semantic, educational-cognitive, communicative, personal self-improvement.

Lesson plan.

1) Preparatory stage.

Repetition of basic knowledge.

1) Checking the assimilation of the material covered frontally (or individually) on the following questions (questions are projected on the screen, to which students answer orally).

1. Define a line perpendicular to a plane.

2. Which line is called inclined to the plane?

3. What is called an inclined projection onto a plane?

4. How is the three perpendicular theorem formulated?

5.How is the angle between a straight line and a plane determined?

2) Theoretical stage.

a) An inclined line is drawn to the plane α, the length of which is 13 cm, the projection of the inclined line is 5 cm. At what distance from the plane is the point from which the inclined line is drawn?

b) The distance from point D to each of the vertices of regular triangle ABC is 15 cm. Find the distance from point D to plane ABC if AB = 10 cm.

3) Practical stage.

Independent application of skills and knowledge.

Carry out independent work in 15 options. (Annex 1)

Bibliography.

1. Alimov Sh.A. and etc.

Mathematics: algebra and principles of mathematical analysis, geometry. Algebra and beginnings of mathematical analysis (basic and advanced levels). 10-11 grades. - M., 2014.

2. Bogomolov N.V.

Mathematics: textbook for applied bachelor's degree / N.V. Bogomolov, P.I. Samoilenko. – 5th ed., revised. and additional – M.: Yurayt Publishing House, 2014.

Annex 1.

Options for independent work.

Option 1

1) Point A does not lie in the plane, but point E belongs to this plane. AE = 13 cm, the projection of this segment onto the plane is 5 cm. What is the distance from point A to this plane?

2)Isosceles triangle ABE is in the α plane. The lateral sides of the triangle ABE are equal to 10 cm, and the side of the base AE = 16 cm. Perpendicular CB, which is equal to 6 cm, and inclined CA and CE are drawn to this plane. Calculate the distance from point C to side AE of the triangle.

3) Through vertex A of a right triangle ABC with right angle C, a line AD is drawn perpendicular to the plane of the triangle, a) Prove that the triangle CBD is right, b) Find BD if BC = 4, DC = 6.

Option 2

1) Straight a intersects the plane β at point C and forms an angle of 30° with the plane. P∈a, point R is the projection of point P onto the plane β. PR=7 cm Find PC.

2)Right triangle MBE (∢M=90°) is in the α plane. BE=13 cm, and ME=12 cm. A perpendicular CB of length 7 cm is drawn to this plane. Calculate the distance from point C to side ME of the triangle.

3) Segment AD is perpendicular to the plane of isosceles triangle ABC. It is known that AB = AC = 5 cm, BC = 6 cm, AD = 12 cm. Find the distances from the ends of the segment AD to the straight line BC.

Option 3

1) An inclined plane is drawn to the plane α, the length of which is 10 cm, the projection of the inclined one is 6 cm. At what distance from the plane is the point from which the inclined line is drawn?

2) Point K is located at a distance of 8 cm from the plane of rectangle ABCD and at equal distances from the vertices of the rectangle.

Calculate at what distance from the vertices of the rectangle point K is located if the lengths of the sides of the rectangle are 24 cm and 18 cm.

3) Through vertex A of rectangle ABCD a straight line AK is drawn, perpendicular to the plane of the rectangle. It is known that KD = 6 cm, KV = 7 cm, KS = 9 cm. Find: a) the distance from point K to the plane of the rectangle ABCD;

Option 4

1) An inclined AB (A∈α) is drawn to the plane α. The length of the inclined one is 18 cm, the inclined one forms an angle of 60° with the plane. Calculate how far point B is from the plane.

2) The distance from point G to each of the vertices of regular triangle ABC is 12 cm. Find the distance from point G to plane ABC if AB = 9 cm.

3) The straight line OK is perpendicular to the plane of the rhombus ABCD, the diagonals of which intersect at point O. Find this distance if OK = 4.5 dm, AC = 6 dm, BD = 8 dm.

Option 5

1) Straight m intersects the plane ß at point A, and forms an angle of 60° with the plane, P∈ m, point R is the projection of point P onto the plane β. PR=9 cm. Find PA.

2) The inclined AD with the α plane forms an angle of 30˚, and the inclined DC with the α plane forms an angle of 45˚. The length of the perpendicular DB is 7 cm. Calculate the lengths of both inclined ones.

3) Through vertex B of square ABCD a straight line BM is drawn, perpendicular to its plane. Find the distances from point M to straight lines containing the sides and diagonals of the square, if BM = 10 dm, AB = 5 dm.

Option 6

1) The length of the segment VB is 10 m. It intersects the plane at point O. The distances from the ends of the segment to the plane are 2 m and 3 m, respectively. Find the acute angle that the segment VB forms with the plane.

2) One of the legs of the right triangle ABC is equal to 5, and the acute angle adjacent to this leg is equal to 60˚. A line CD is drawn through the vertex of right angle C, perpendicular to the plane of this triangle, CD = 8. Find the distance from point D to line AB.

3) From point A, at a distance of 5 cm from the plane ß, inclined AB and AC are drawn to this plane at an angle of 30° to the plane. Their projections onto the ß plane form an angle of 120°. Find the sun.

Option 7

1) The projections of the inclined AD and DC on the α plane are equal to 4 cm and 10 cm, respectively, and the angle between them is 60°. Calculate the distance between the ends of the oblique projections.

2) Point M is located at a distance of 10 cm from the plane of rectangle ABCD and at equal distances from the vertices of the rectangle.

Calculate at what distance from the vertices of the rectangle point M is located if the lengths of the sides of the rectangle are 12 cm and 5 cm.

3) One end of this segment lies in the α plane, and the other is located at a distance of 11 cm from it. Find the distance from the middle of this segment to the α plane.

Option 8

1) An inclined CD (C∈α) is drawn to the plane α. The length of the inclined one is 16 cm, the inclined one forms an angle of 30° with the plane. Calculate how far point D is from the plane.

2) Through vertex B of square ABCD a line BF is drawn, perpendicular to its plane. Find the distances from point F to the lines containing the sides and diagonals of the square, if BF = 8 dm, AB = 4 dm.

3) The segment KD is perpendicular to the plane of the isosceles triangle KPE. It is known that KP = KE = 4 cm, PE = 8 cm, KD = 14 cm. Find the distances from the ends of the segment KD to the straight line PE.

Option 9

1) The inclined AM drawn from point A to a given plane is 7 cm. What is the projection of this inclined plane onto the plane if the angle between straight line AM and this plane is 30°?

2) The distance from point N to each of the vertices of a regular triangle ABC is 5 cm. Find the distance from point N to plane ABC if AB = 8 cm.

3) Through vertex A of rectangle ABCD a straight line AK is drawn, perpendicular to the plane of the rectangle. It is known that KD = 6 cm, KV = 7 cm, KS = 9 cm. Find the distance between straight lines AK and CD.

Option 10

1) The inclined line AM drawn from point A to the given plane is equal to 15. What is the projection of this inclined line onto the plane if the angle between the straight line AM and the given plane is 60°.

2) Line BD is perpendicular to the plane of triangle ABC. It is known that BD = 9 cm, AC = 10 cm, BC = BA = 13 cm. Find the distance from point D to straight line AC

3) Point M is located at a distance of 10 cm from the plane of rectangle ABCD and at equal distances from the vertices of the rectangle.

Calculate at what distance from the vertex of the rectangle point M is located if the lengths of the sides of the rectangle are 16 cm and 10 cm.

Option 11

1) An inclined line is drawn at an angle φ to the plane α. Find φ if it is known that the oblique projection is half the size of the oblique itself.

2) Through the vertex of right angle C of an isosceles right triangle ABC, a straight line CM is drawn, perpendicular to its plane. Find the distance from point M to line AB if AC = 4 cm and CM = 2 √7 cm.

3) Line BD is perpendicular to the plane of triangle ABC. It is known that BD = 9 cm, AC = 10 cm, BC = BA = 13 cm. Find the area of triangle ACD.

Option12

1) The projections of the inclined AM and MC onto the α plane are equal to 5 cm and 8 cm, respectively, and the angle between them is 45°.

Calculate the distance between the ends of the inclined projections

2) Line OK is perpendicular to the plane of the rhombus ABCD, the diagonals of which intersect at point O. Prove that the distances from point K to all lines containing the sides of the rhombus are equal

3) A straight line MF is drawn through the vertex M of the square MNOR, perpendicular to its plane. Find the distances from point F to the lines containing the sides and diagonals of the square, if MF = 12 dm, MN = 6 dm.

Option 13

1) One end of this segment lies in the ß plane, and the other is located at a distance of 12 cm from it. Find the distance from the middle of this segment to the ß plane.

2) Point P is located at a distance of 12 cm from the plane of rectangle ABCD and at equal distances from the vertices of the rectangle.

Calculate at what distance from the vertices of the rectangle point P is located if the lengths of the sides of the rectangle are 8 cm and 6 cm.

3) The projections of the inclined MN and MK on the α plane are equal to 8 cm and 12 cm, respectively, and the angle between them is 30°. Calculate the distance between the ends of the oblique projections.

Option 14

1) The inclined AM drawn from point A to a given plane is 8 cm. What is the projection of this inclined plane onto the plane if the angle between straight line AM and this plane is 45°?

2) Through vertex B of the rhombus ABCD a straight line BM is drawn, perpendicular to its plane. Find the distances from point M to the lines containing the sides of the rhombus, if AB = 25 cm, ∠BAD = 60°, BM = 12.5 cm.

3) From point A, which does not belong to the plane α, a perpendicular AO and two inclined ones AB and AC are drawn to this plane. It is known that ∠OAB= ∠BAС = 60°, AO = 1.5 cm. Find the distance between the inclined bases.

Option 15

1) The ends of the segment are separated from the plane α at distances of 3 cm and 7 cm. Find the distance from the middle of the segment to the plane α.

2) The distance from point M to each of the vertices of a regular triangle ABC is 4 cm. Find the distance from point M to plane ABC if AB = 6 cm.

3) The inclined NM drawn from point H to a given plane is equal to 9 cm. What is the projection of this inclined plane onto the plane if the angle between the straight line NM and the given plane is 45°?