Working with multi-digit numbers
The 4th grade program offers a more complex process of division with increasing calculated numbers. If in the third grade calculations were carried out on the basis of a basic multiplication table ranging from 1 to 10, then fourth graders carry out calculations with multi-digit numbers over 100.
It is most convenient to perform this action in a column, since the incomplete quotient will also be a two-digit number (in most cases), and the column algorithm simplifies the calculations and makes them more visual.
Divide multi-digit numbers into two-digit numbers : 386:25
This example differs from the previous ones in the number of calculation levels, although the calculations are carried out according to the same principle as before. Let's take a closer look:
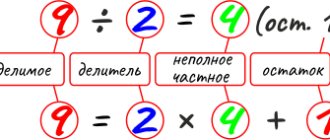
386 is the dividend, 25 is the divisor. It is necessary to find the incomplete quotient and select the remainder.
First level
The divisor is a two-digit number. The dividend is three-digit. We select the first two left digits of the dividend - this is 38. We compare them with the divisor. Is 38 more than 25? Yes, that means 38 can be divided by 25. How many whole 25 are in 38?
25*1=25, 25*2=50. 50 is more than 38, let's go back one step.
Answer - 1. We write the unit in the zone of incomplete quotient .
Further:
38-25=13. Write the number 13 below the line.
Second level
Is 13 more than 25? No - that means you can “lower” the number 6 down by adding it next to 13, on the right. It turned out to be 136. Is 136 more than 25? Yes - that means you can subtract it. How many times can 25 fit into 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 is more than 136 – we go back one step. We write the number 5 in the incomplete quotient zone, to the right of one.
Calculate the remainder:
136-125=11. Write it below the line. Is 11 more than 25? No - division cannot be carried out. Does the dividend have digits left? No - there is nothing more to share. The calculations are completed.
Answer: the partial quotient is 15, the remainder is 11.
What if such a division is proposed, when the two-digit divisor is greater than the first two digits of the multi-digit dividend? In this case, the third (fourth, fifth and subsequent) digit of the dividend takes part in the calculations immediately.
Here are examples of division with three- and four-digit numbers:
386:75
75 is a two-digit number. 386 – three-digit. Compare the first two digits on the left with the divisor. 38 is more than 75? No - division cannot be carried out. We take all 3 numbers. Is 386 more than 75? Yes, division can be done. We carry out calculations.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 is more than 386 – we go back a step. We write 5 in the incomplete quotient zone.
Find the remainder: 386-375=11. 11 is more than 75? No. Are there any digits left for the dividend? No. The calculations are completed.
Answer: partial quotient = 5, remainder 11.
119:35
Let's check: is 11 more than 35? No - division cannot be carried out. Let's substitute the third number - 119 is more than 35? Yes, we can carry out the action.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 is more than 119 - we go back one step. We write 3 in the incomplete balance zone.
Find the remainder: 119-105=14. Is 14 over 35? No. Are there any digits left for the dividend? No. The calculations are completed.
Answer: partial quotient = 3, 14 left.
1195:99
Let's check: is 11 greater than 99? No, we substitute another number. Is 119 more than 99? Yes - let's start the calculations.
11<,99, 119>,99.
99*1=99, 99*2=198 – overkill. We write 1 in the incomplete quotient.
Find the remainder: 119-99=20. 20<.99. We omit 5. 205>.99. Let's calculate.
99*1=99, 99*2=198, 99*3=297. Too much. We write 2 in the incomplete quotient.
Find the remainder: 205-198=7.
Answer: partial quotient = 12, remainder 7.
Division with remainder examples
Learning to divide by column with a remainder
Math lesson notes in 3rd grade
Summary of a mathematics lesson in grade 3 “Division with a remainder”
Goal: to teach an algorithm for dividing numbers with a remainder and to teach how to apply the acquired knowledge in practice.
Tasks:
Educational: develop the ability to solve word problems, perform division with a remainder, improve oral and written counting skills.
Educational: to develop observation and curiosity, a love of mathematics and learning in general, to form a culture of students’ speech, skills to work in a team, in pairs.
Developmental: develop attentiveness, thinking, accuracy, creative skills and spatial imagination.
Planned results:
Regulatory: create opportunities for learning and organizing your activities; the ability to accept goals and follow them in educational activities; ability to plan your activities and their complexity; the ability to interact with classmates and the teacher in educational activities; develop determination and perseverance in achieving goals; willingness to overcome difficulties.
Communication: developing constructive interaction skills, learning the rules of interaction in a group: speak in turns, do not interrupt, listen to your interlocutor; teach to understand the possibility of different positions and points of view.
Cognitive: development of cognitive interests; readiness to accept and solve educational and cognitive tasks; ability to highlight the principles of the division with remainder algorithm; learn to compare data; identify common resources, classify problem solving through modeling; correlate the results obtained on the model with reality (with texts).
Personal: understanding of basic moral norms: mutual support, responsibility; development of cognitive interests, educational motivation.
Equipment: textbook “Mathematics 3rd grade” by Moro, cards with the division algorithm with a remainder, emoticons, cards with tasks for class work, cards of 3 levels of difficulty for homework.
During the classes
- Organizing time:
There are 3 emoticons on the board (smiling, sad and calm)
— Which smiley matches your mood?
— A sign of a good mood is a smile. Smile at me and at yourself.
“I would like this mood to persist until the end of the lesson.” Good luck everyone.
— Guys, we try to discover new knowledge for each lesson. Today's lesson is no exception. During the lesson we will try to expand our mathematical knowledge, and for this I suggest moving on to the "X-pedition".
— What is X in mathematics? (unknown that needs to be found.)
- We must do research, learn something new today, because there is still a lot of things unknown to us in mathematics.
2. Updating knowledge, problem statement:
To warm up and be successful in our lesson, I suggest you complete the tasks on the cards:
Grandma is 54 years old, and Petya is 9 times younger. How old is Petya?
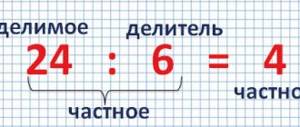
54 : 9 = 6
Masha studies 5 days a week. She has 25 lessons. How many lessons does Masha have every day?
25:5=5
Mom baked 32 pies for a family of 8 people. How many pies will each person get?
32:8=3
Children in groups decide orally, writing down only the answers on sheets of paper. Then representatives of the groups also come out and voice their results.
In completing this task, what arithmetic operation did we use today? What is the topic of the lesson? (DIVISION)
Do you think we already know everything about division?
- Formulation of the problem. Learning new material:
To answer the question, let's try to solve the problem:
There were 7 tickets for the concert at the box office. How many people will be able to buy tickets if everyone buys two tickets?
To answer the question of the problem, let's solve it. How to solve it?
(you need to divide 7 by 2)
Well let's try. How much do we get if we divide 7 by 2? (children can answer that it is impossible to divide 7 by 2, it doesn’t work, offer other solutions or say that the problem cannot be solved, the numbers are not correct). Well, a problem has arisen in our X-pedition.
But if such a problem exists, then it is still possible to solve it. Let's return to our question - do we know everything about division? What do you think will be the purpose of our lesson? (learn a new division technique).
So, in the table of multiplication by 2 there is no product equal to 7, in other words, there is no integer so that when multiplied by 2xX the result is 7. What to do? (make a drawing or diagram - we call one student to the board, he draws 7 tickets, or draws a segment divided into 7 parts). Here we have 7 tickets. Each person buys 2 tickets. How to show this? (combine 2 tickets)
What do we see? (if each person buys 2 tickets, then only 3 people will buy tickets, and there will be 1 more ticket left)
When you divide 7 by 2 you get 3 with a remainder of 1. This division is usually called division with a remainder and is written 7:2=3 (remainder 1). read the entry like this: “7 divided by 2, you get 3 and 1 remainder,” or “Dividend 7, divisor 2, quotient 3, remainder 1” (practice - repeat with the whole class, in rows, ask the children to read the entry one by one).
To remember the correct reading of such a complex action, let’s complete task No. 1 in the textbook on page 26.
4. physical exercise “Captain Crab - Do this!”
5. Consolidation and assimilation of new knowledge:
- and now let’s do some practical work; we need to place the kittens in baskets. How can I do that?
- Complete the drawing. Write the expression in your notebook.
— Butterflies flew into the clearing. Let's try to plant them on flowers.
- Complete the drawing. Write the expression in your notebook.
(Each time we look at what number was divided, why such a remainder was obtained)
How can you solve examples of division with a remainder without doing the drawings every time?
What do you think will help us?
(Algorithm)
(cards with the algorithm were distributed to children)
Using our algorithm, let's complete the tasks in the textbook.
Complete tasks 2,3,4 in the textbook on page 26.
6. Lesson summary, reflection:
What discovery did we make today in our X-pedition? Do we need this new knowledge?
Do you think we achieved the goal of our lesson?
Raise your hand for those who found it easy during the lesson and everything was clear? (those who experienced difficulties, those who found it very difficult)
The lesson is useful, everything is clear. There's just one thing that's a little unclear. You still have to work hard. Yes, it’s still difficult to study!
7. Homework:
Level 1 of difficulty (for those who found it very difficult during the lesson): textbook, p. 26 No. 5
- difficulty level (for those who had difficulties), card:
The numbers given are: 2,3,7,0,4,5,9,8,1,6,17,14,13,15,16,19,36,37. First write down those that are divisible by 2 without a remainder, and then write down on another line those that, when divided by 2, give a remainder.
Perform division with remainder using the multiplication table: 17:2, 35:9, 5:2, 19:9, 9:2, 67:9, 15:2, 3:2.
- difficulty level (for those who found it easy during the lesson):
Knowing that:
- 14:7=2, divide with the remainder 15:7, 16:7, 17:7, 18:7
What other numbers can you divide with the remainder based on the equality 14:7=2?
- 0:8=0, divide with the remainder: 1:8, 2:8, 3:8; Come up with the rest of the numbers for division with a remainder yourself.