Signs of equality of triangles
One wise man said: >. The triangle is a unique unit of knowledge of geometry. It has many properties unique to it, and at the same time its research has led scientists to numerous generalizations for polygons. A triangle is a geometric figure consisting of three points that do not lie on the same straight line, connected by segments.
Historical information about the signs of equality of triangles
Tests for the equality of triangles have long been of great importance in geometry, since the proof of numerous theorems was reduced to proving the equality of certain triangles. The Pythagoreans were already engaged in proving the signs of equality of triangles. According to Proclus, Eudemus of Rhodes attributes to Thales of Miletus a proof of the equality of two triangles having equal sides and two angles adjacent to it (the second sign of the equality of triangles).
Thales used this theorem to determine the distance from the shore to sea ships. It is not known exactly what method Thales used to do this. It is believed that his method was as follows: let A be a point on the shore, B a ship at sea. To determine the distance AB, a perpendicular of arbitrary length AC AB is restored on the shore; in the opposite direction, restore CE AC so that points D (the middle of AC), B and E are on the same straight line. Then CE will be equal to the desired distance AB. The proof is based on the second criterion for the equality of triangles (DC = DA; C = A; EDC = BDA as vertical).
In the first stages of its development, geometry was a set of useful, but unrelated rules and formulas for solving problems that people encountered in everyday life. Only many centuries later, scientists of Ancient Greece created the theoretical basis of geometry. But even then, applied geometry did not lose its importance, since it was indispensable for land surveying, navigation and construction. Thus, written in antiquity, manuals on geometry, containing > solutions to practical problems, have accompanied humanity throughout the entire history of existence. Solutions to certain ancient problems of a practical nature can still be used today, and therefore deserve attention.
The history of geometry stores many techniques for solving problems of finding distances. Determining the distances to ships at sea is one such problem, which can be solved in two ways.
It is believed that both methods of solving it belong to the ancient Greek scientist, traveler and merchant Thales of Miletus (VI century BC)
The first method is based on one of the signs that triangles are equal.
Triangles are equal in side and two adjacent angles.
The first sign of equality of triangles. If two sides and the angle between them of one triangle are equal, respectively, to two sides and the angle between them of another triangle, then such triangles are congruent.
The second sign of equality of triangles. If a side and its adjacent angles of one triangle are equal, respectively, to a side and its adjacent angles of another triangle, then such triangles are congruent.
The third sign of equality of triangles. If three sides of one triangle are equal to three sides of another triangle, then such triangles are congruent.
Practical problems
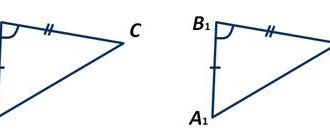
Problem 1: If there is an obstacle between points A and B, then the distance AB can be found as follows. Select point C, from which points A and B are visible, and draw straight lines AC and BC. Set aside CA1=CA, CB1=CB. Distance A1B1 will be equal to the required distance. Prove it
Solution: If CA1=CA, and CB1=CB, Angles BCA and A1CB1 are equal because they are vertical, hence triangles ABC and A1B1C are equal on 2 sides and the angle between them, then AB=A1B1
Task 2: To determine the distance from point B to the inaccessible point A, draw an arbitrary straight line BC, measure the angles ABC and BCA and, having built them on the other side of the straight line BC, draw straight lines BD and CD. Prove that the distance BD is equal to the required distance AB.
Solution: BC - Common side, since on the other side of straight line BC angles ABC and ACB were put aside, new angles were formed, DBC and DCB. Angles ABC and DBC are equal, angles ACB and DCB are equal, hence triangles ABC and DBC are equal in side and two adjacent angles, which means AB = DB
Problem 3: Three villages B, C and D are located so that C is 7 km southwest of village B, and village D is 4 km east of B. Three other villages A, K and M are located so that the village M is located 4 km south of K, and the village A is 7 km southeast of M. Prove that the distance between points C and D is the same as between points K and A
Solution: Let's agree that on the map north (N) is directed up, south (S) is down, east (O) is to the right, and west (W) is to the left. According to this condition, villages B, C and D are located as shown in the figure. Moreover, BD = KM = 4 km, BC = MA = 7 km and ∠SVD = ∠KMA = 1350. Then ∆DBC = ∆KMA, therefore, DC = AK.
Task 4: When building roofs, bridges, and cranes, support beams or beams are fastened so that they form a system of triangles. Why does this arrangement of beams better ensure the rigidity of the structure’s shape than another?
Solution: Because this type of fastening is more reliable. It can withstand more loads than the other. A triangle is a rigid figure.
Task 5 One of its corners broke off from a triangular window glass. Is it possible to order a glazier to cut the same window glass from the existing part? What dimensions should be taken?
Solution: Measure the length of the chip and the angles. The task comes down to constructing a triangle using a side and two angles.
Signs of equality of triangles help in solving construction problems, for example: constructing an angle equal to a given one; constructing an angle bisector
Conclusion
After completing this project, I learned how to find solutions to practical problems using triangle equalities.
TECHNOLOGICAL MAP OF A GEOMETRY LESSON IN 7TH GRADE ON THE TOPIC “The second sign of equality of triangles”
author: Dudko Yulia Alexandrovna
mathematics teacher at MBOU "Secondary School No. 2" in the village of Bussevka, Spassky district, Primorsky Territory
TECHNOLOGICAL MAP OF A GEOMETRY LESSON IN 7TH GRADE ON THE TOPIC “The second sign of equality of triangles”
TECHNOLOGICAL MAP OF A GEOMETRY LESSON IN 7TH GRADE ON THE TOPIC “The second sign of equality of triangles”
LESSON PLAN
| Full name (full name) | Dudko Yulia Alexandrovna |
| Place of work | MBOU "Secondary School No. 2" of the village of Bussevka |
| Job title | Teacher |
| Item | Mathematics |
| Class | 7 |
| Topic and lesson number in the topic | The second criterion for the equality of triangles (lesson No. 1) |
| Subject program and its author | Geometry 7-9, L.S.Atanasyan. |
| Lesson Objectives | 1) educational : familiarize students with the second sign of equality of triangles; 2) developing : development of attention, logical thinking, ability to solve educational problems; 3) educational : developing interest in geometry, cultivating a mathematical culture of writing and speech |
| Lesson type | A lesson in gaining new knowledge and ways of acting. |
| Technologies (elements) | Development of critical thinking, problem-dialogical learning, health-saving. |
| Methods and forms | Methods: partial search, problem-based. Forms of work: group, frontal, individual; oral, written. |
| Necessary equipment | Finished drawings, presentation, textbook. Projector. |
| Planned results | ||
| Subject | Universal learning activities (UAL) | Personal |
Subject:
| Metasubject: educational – be aware of the cognitive task; read and listen, extracting the necessary information, understand information, perform educational and cognitive actions; be able to navigate your knowledge system, distinguish the new from the already known. regulatory – accept the learning task; plan (in collaboration with the teacher and classmates or independently) the necessary actions, operations, act according to the plan; be able to pronounce the sequence of actions in the lesson, express your guess communicative – defending your point of view, | Personal: be able to carry out self-assessment based on the criterion of successful educational activities, focus on success in educational activities, the desire to acquire new knowledge, skills, and improve existing ones; be aware of your difficulties and strive to overcome them. |
Organizational structure of the lesson.
| Lesson stage | Contents of teacher activities | Content of students’ activities (actions performed) | Formed methods of activity |
| 1. Organizational stage | |||
| 2. Setting the goals and objectives of the lesson. Motivation for students' educational activities | |||
| 3. Checking homework | |||
| 4. Updating knowledge | Organizes work in pairs to review the theory: 1. Determination of adjacent and vertical angles and their properties. 2. The first sign of equality of triangles. 3. Determination of the median, height, bisector of a triangle. Solving oral problems: 1) In Fig. 1 DE = 2) OB = | Repetition of the theory (adjacent, vertical angles, 1 sign of equality of triangles, median, height, bisector) Oral tasks based on ready-made drawings | Participate in dialogue, understand the point of view of the interlocutor, select arguments to answer the question posed, give examples |
| 5. Learning new material | Formulation of the problem: Given: ∆ ABC , ∆ MNK , AB = MN=4cm , ∠ A = ∠ M=550 , ∠ B = ∠ N=450 . Draw Δ Discussion of the need to introduce new knowledge. Proof of the equality ∆ MNK = ∆ | There is a discussion of the practical task. Students answer questions asked by the teacher Construction: 1) set aside segment MN = 4 cm, since ∆ 2) build ∠ NMP = 55°; 3) construct ∠ MNE = 45° on the same side of straight line 4) MR ∩ Formulate the topic of the lesson and its purpose. Write down the topic of the lesson. Reading the theorem from the textbook, p.40. clause 19. | |
| Physical education minute | |||
| 6. Primary consolidation of new material | Organizes work in groups to memorize the formulation of 2 signs of equality of triangles (differentiated approach) | Work in pairs to consolidate the formulation of 2 signs of equality of triangles. | |
| Organizes oral solution of problems based on ready-made drawings. Prove the equality of triangles: 1) Fig.1 Prove that ∆ ABC = ∆ 2)Fig.2 Prove that ∆ ВСD = ∆ Organizes demonstrations of problem solving on the board. | Front work on improving problem solving skills on a studied topic They learn to reason and argue independently. They learn to reason and argue independently. Write down solutions to problems. Written solution to the problem textbook: No. 122 | ||
| Organizes individual work for students. Then organizes a self-test of the solution according to the sample provided by the teacher on the screen. | Individual work: learn to reason independently and write down the solution to a problem in a notebook. textbook: No. 124 | ||
| 8. Reflection on learning activities in the lesson | Summing up the lesson, asks students to continue saying about the lesson: • During the lesson it was important for me... • It was difficult for me in class... • The lesson helped me think... | Continue the statements suggested by the teacher. | |
| 9. Homework | Textbook: learn the proof of the theorem from paragraph 19, solve problem No. 123. | Completing tasks | |
Introspection of a geometry lesson,
conducted by a mathematics teacher at MBOU “Secondary School No. 2” in the village of Bussevka
Dudko Yulia Alexandrovna.
Lesson topic: “The second sign of equality of triangles”
Didactic goal:
create conditions for the formation of new educational information.
Content goals:
educational:
create conditions for perception, comprehension of the second sign of equality of triangles, prove the theorem; teach how to solve problems using new material;
developing:
create conditions for the development of the ability to analyze, compare, generalize, draw conclusions, build logical chains, develop attention, skills of working in pairs;
educational:
develop cognitive interest, promote students’ understanding of the need for intellectual effort for successful learning, the positive effect of persistence in achieving a goal, and develop communication skills.
Lesson type:
discovery of new knowledge.
Lesson construction technology:
problem-dialogical
Methods:
by sources of knowledge:
verbal, visual;
according to the degree of teacher-student interaction:
heuristic conversation;
regarding didactic tasks:
preparation for perception;
regarding the nature of cognitive activity:
systemic didactic approach, partial search method.
Equipment:
textbook: Geometry. Grades 7-9: textbook for general education institutions L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al., 20th edition - M.: Education, 2020. , board, chalk.
The triune goal of the lesson provides for the interconnection of educational, training and developmental components, clearly stated educational, developmental and educational goals of the lesson which, in my opinion, are fully consistent with the content of the program material on this topic, the type of lesson, its place in the system of lessons on the topic and are aimed at active the activities of students in the formation and development of the concept of “the second sign of equality of triangles”, the ability to solve problems with practical content, the development of mathematical thinking, and the culture of mathematical speech.
All the goals of the lesson, in my opinion, are relevant and were in the zone of proximal development of children, which was clearly visible through the tasks and questions that were asked both at the basic and creative levels, taking into account the individual characteristics of the students.
The structure of the lesson corresponded to its purpose and type (lesson of discovering new knowledge). I tried to constantly maintain the logical sequence and interconnection of all stages of the lesson, expediently distribute time among the stages of the lesson, and tried to rationally use the equipment of the office in which the lesson was held. I believe that I chose the optimal pace of the lesson, which took into account the characteristics of the class, a clear lesson plan, the content of the tasks offered to the children, and allowed me to fully realize all the assigned tasks and goals of the lesson.
I believe that all stages of the lesson (organizational stage, setting the goal and objectives of the lesson, motivating students’ learning activities, updating knowledge, initial assimilation of new knowledge, initial testing of understanding, initial consolidation, information about homework, instructions on how to complete it. Reflection fully met the requirements Federal State Educational Standards LLC to the structure of a lesson of this type.
I think that I was able to ensure students’ motivation and acceptance of the goals of educational and cognitive activity, and updated the basic knowledge and skills of schoolchildren. At the main stage, I was able to provide generalization, comprehension and systematization of knowledge and methods of action on the topic “The second sign of equality of triangles” at the reproductive and constructive level.
The content of the lesson, in my opinion, meets the requirements of the standard. The presentation of the lesson material was logical, accessible, scientific, with maximum involvement of students in mastering the topic of the lesson.
I believe that I was able to optimally select methods, techniques and teaching aids, taking into account:
- lesson topics;
- lesson objectives;
- class capabilities;
- educational and material base;
- the content of the didactic task.
Teaching methods: problem presentation, encouragement to search for alternative solutions - contributed to the formation in students of independent thinking, active learning activities, an active life position, and the ability to defend their point of view.
Active cognitive activity of schoolchildren was realized through various forms of work in the classroom: frontal, individual, group (in pairs), independent, practical.
I believe that the program material of the lesson was mastered by all students. The alternation of verbal, practical methods, and various forms of organizing cognitive activity helped prevent students from being overloaded during the lesson.
Reflection showed that all children were satisfied with their success, work in the lesson, and friendly environment, and positive cooperation with the teacher and classmates was especially noted. The nature of the homework is feasible for all students; they were prepared for its completion throughout the lesson.
Conclusion: the lesson achieved its goal; it represents a holistic system with a full set of elements.
The connections between didactic tasks, the content of educational material, methods and forms of teaching are strong and ensure the optimal functioning of the entire lesson system. The lesson meets modern requirements for a mathematics lesson. TECHNOLOGICAL MAP OF A GEOMETRY LESSON IN 7TH GRADE ON THE TOPIC “The second sign of equality of triangles”
Technological map of the lesson “The third sign of equality of triangles”
Technological map of geometry lesson, 7th grade
Author: Gerasina Natalya Alexandrovna
Description of material:
technological map of a geometry lesson on the topic “The third sign of equality of triangles” for 7th grade students. This topic is studied after introducing the concept of equality of triangles and two signs of equality of triangles. The material will be useful for teachers, since the technological lesson map is a modern form of planning the pedagogical interaction between teacher and student; modern methods and technologies are used in the lesson.
Subject:
The third sign of equality of triangles.
Goals:
— Personal:
development of intellectual abilities, independence in work, hard work, accuracy, speech development, ability to think, analyze, generalize, express one’s thoughts clearly and concisely.
— Metasubject:
the formation of information, communicative and educational competence of students, the ability to generalize, analyze, compare concepts, and the formation of the ability to draw conclusions. The ability to determine the purpose of educational activities, listen to the interlocutor, formulate one’s own opinion and position.
— Subject:
formation of knowledge and skills in proving the theorem and solving simple problems on the topic.
Lesson type:
lesson on learning new material
Learning objectives aimed at student development:
- in a personal direction:
provide cognitive motivation for students when learning new concepts, development of attention, memory, logical and creative thinking.
- in the meta-subject direction:
development of thinking operations (comparisons, generalizations), formation of individual components of research activity (ability to observe, ability to draw conclusions, reflect).
- in the subject area:
application of the third sign of equality of triangles to problem solving, consolidation of skills in solving problems on this topic, formation of skills to manage one’s educational activities, formation of interest in mathematics, formation of motivation by setting cognitive tasks, revealing the connection between theory and experience.
Technical support:
from the teacher:
textbook “Geometry. 7-9 grades”, Atanasyan L.S. etc., computer, projector, interactive whiteboard, presentation, YouTube video, multi-colored paper triangles.
for each student:
textbook “Geometry. 7-9 grades”, Atanasyan L.S. etc., notebook, ruler, pencil, diary.
Lesson structure and flow:
| № | Lesson stage | Activity teachers | Student activities | UUD | EOR | Time |
| 1 | Organizing time | Greets students and organizes work space | Greet the teacher, organize their workplace, demonstrate readiness for the lesson | 2 minutes. | ||
| 2 | Updating of reference knowledge | Asking questions: - Which figures are called equal? - What is a sign? — Why do I use the signs of equality of triangles? -What signs of equality do you know? State them. | They answer the teacher’s questions and get involved in the work during the lesson. | Personal UUD: show interest in studying the topic, the need to study further Communicative UUD: planning a learning task | 3 min | |
| 3 | Motivational target moment | Divides students into groups. Each group is offered multi-colored triangles of different sizes, some of which are equal. - Find equal triangles. - Pay attention to the sides of equal triangles. What can you say about them? - Indeed, the sides of the triangles are equal. Therefore, in this lesson we will learn another criterion for the equality of triangles. Informs the topic of the lesson. | Consider triangles. Groups of equals are identified. They answer the question and draw conclusions. Write down the topic in your notebook | Personal UUD: show interest in new content. Cognitive UUD: formulate an information request, formulate interest in studying a new topic, independently highlight and formulate a cognitive goal; Regulatory UUD: goal setting. | Topic on the interactive whiteboard | 5 minutes |
| 4 | Indicative stage | Invites students to prove the third sign of equality of triangles — How can you use the third criterion for the equality of triangles? — From the sign that triangles are equal, it follows that a triangle is a rigid figure. Suggests looking at Figure 71, 72 in the textbook, which shows how it is used in practice. | Together with the teacher, they prove the third sign of equality of triangles. Students draw a conclusion. They answer where the sign can be applied. They work with the textbook, draw conclusions, express their own opinions. | Cognitive UUD: building a logical chain of reasoning; proof. Regulatory management control: control, correction, summing up. Communicative: the ability to express one’s thoughts with sufficient completeness and accuracy. | Drawing for the theorem on the interactive whiteboard | 10 min |
| 5 | Reflection | Offers videos from YouTube. A story that students wrote about the third criterion for the equality of triangles. Video: https://www.youtube.com/watch?v=qPaKCGK8i-A | Watch the video, repeat the third sign | Cognitive UUD: memorization, reflection. | 2 minutes | |
| 6 | Primary consolidation | Sets the task to prove the equality of the triangles behind the pictures. | Solve standard tasks orally on a new sign with pronouncing the rules | Cognitive UUD: conscious construction of a speech utterance in oral form | Drawings on the interactive whiteboard | 10 min |
| 7 | Practical stage | Offers to solve problems from textbook No. 135, 138 in writing. Draws attention to the correct formulation of mathematical terms. Offers exercise LearningApps. You need to distribute the triangles into groups. https://learningapps.org/611950 | Solve problems and write down solutions in notebooks. Take turns going to the board and writing down the main points of the solution. Distribute equal triangles accordingly to the sign. | Cognitive UUD: conscious construction of speech utterances in written and oral form. Regulatory UUD: monitoring the correctness of students’ answers. Communicative: The ability to express one’s thoughts with sufficient completeness and accuracy, listen and engage in dialogue. | Exercise on the interactive whiteboard | 10 min |
| 7. | Reflective-evaluative stage | Offers the exercise “Sack of Knowledge”. Recording and commenting on homework | They write down on small pieces of paper what they learned in the lesson and put it in their bag. Assess the degree to which the goal has been achieved Write homework in a diary | Regulatory: self-regulation, communicative Using criteria to support your judgment | 3 min |