Perpendicularity of lines and planes Geometry Grade 10 Lesson 1. - presentation
Perpendicularity of lines and planes Geometry Grade 10 Lesson 1
Plan Perpendicular lines in space Perpendicular lines in space Determination of a line perpendicular to a plane Determination of a line perpendicular to a plane Parallel lines perpendicular to a plane Parallel lines perpendicular to a plane Sign of perpendicularity of a line and a plane Sign of perpendicularity of a line and plane
Homework: Textbook paragraphs 15 – 17 Textbook paragraphs 15 – 17 (point 16 without evidence) (point 16 without evidence) 117, , 128
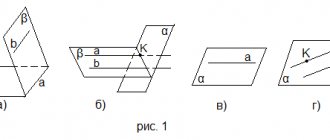
Remember The relative position of lines in space The relative position of lines in space Definition of parallel lines Definition of parallel lines Mutual position of a line and a plane Mutual position of a line and a plane Sign // of a straight line and a plane Sign of // a straight line and a plane
Remember the Isosceles triangle and its properties. The isosceles triangle and its properties. The perpendicular bisector. Perpendicular bisector. Properties of points of the perpendicular bisector Properties of points of the perpendicular bisector A B
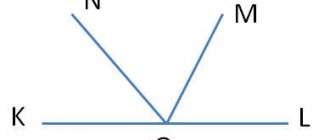
Perpendicular lines Two lines in space are called perpendicular if the angle between them is 90. Two lines in space are called perpendicular if the angle between them is 90.
Think about what the relative position of perpendicular lines could be? What can be the relative position of perpendicular lines? Perpendicular lines can be either intersecting or crossing. Give examples
Problem A B C DD 1 C 1 A 1 Angle BAD = 90 Prove that DC B1 C1 AB A1D1
Lemma If one of two parallel lines is perpendicular to the third line, then the other line is also perpendicular to this line. If one of two parallel lines is perpendicular to the third line, then the other line is perpendicular to this line. GIVEN: a // in, a c GIVEN: a // in, a c Prove: in c Prove: in c
Proof GIVEN: a // in, a c Prove: in c Proof: a in c in//a, a // A M, therefore in// M A So in//M A, s // M S, angle A M C = 90, which means the angle between b and c = 90, i.e. in with
Problem A B C DD 1 C 1 A 1 Angle BAD = 90 Prove that DC B1 C1 AB A1D1
Lines perpendicular to a plane DEFINITION A line is called perpendicular to a plane if it is perpendicular to any line lying in this plane A line is called perpendicular to a plane if it is perpendicular to any line lying in this plane a β β
THINK What could be the relative position of a straight line and a plane if they are perpendicular? What can be the relative position of a straight line and a plane if they are perpendicular? Give examples from the environment that illustrate the perpendicularity of a straight line and a plane
Is it true? If line a is perpendicular to the plane, then it is perpendicular to line AB lying in the plane. If line a is perpendicular to plane β, then it is perpendicular to line AB lying in plane β
Problem Points A, M, O lie on a line perpendicular to the plane. Points A, M, O lie on a line perpendicular to the β plane, and points O, B, C and D lie in the β plane. Make a drawing Which of the following angles are right angles: AOB, MOS, DAM, DOA, VMO?
The connection between // straight lines and their perpendicularity to the plane. Theorem If one of two // lines is perpendicular to a plane, then the other line is perpendicular to this plane. If one of two // lines is perpendicular to a plane, then the other line is also perpendicular to this plane.
The connection between // straight lines and their perpendicularity to the plane. Theorem If two lines are perpendicular to a plane, then they are parallel. If two lines are perpendicular to a plane, then they are parallel. Make a drawing
Sign of perpendicularity of a line and a plane Theorem If a line is perpendicular to two intersecting lines lying in a plane, then it is perpendicular to this plane a
a O P qm GIVEN: a p, a q? PROVE: a β β a L
pq L a ABPQL
pq L a ABPQL O
Problem Line MB is perpendicular to sides AB and BC of triangle ABC. Determine the type of triangle MVD, where D lies on the line AC A B C M D
So.. A line is called perpendicular to a plane if... If two lines are perpendicular to a plane, then they... If one of two parallel lines is perpendicular to a plane, then...
Is it true? If line a is parallel to a plane, and line b is perpendicular to this plane, then lines a and b are mutually perpendicular?
Parallelism and perpendicularity of lines and planes in space
Two lines in space are called parallel if they lie in the same plane and do not intersect. Lines that do not intersect and do not lie in the same plane are called intersecting . A straight line and a plane in space are called parallel if they do not intersect.
A line is parallel to a plane if it is parallel to some line lying in this plane.
Two planes are said to be parallel if they do not intersect.
If two parallel planes are intersected by a third plane, then the direct intersections of the planes are parallel. Through a point not lying in a given plane, it is possible to draw a parallel plane, and only one.
, because
The segments of parallel lines between parallel planes are equal.
= =
Lines in space are called perpendicular if they intersect at right angles. A line intersecting a plane is called perpendicular to this plane if it is perpendicular to any line in the plane passing through the point of their intersection.
A line intersecting a plane is perpendicular to the plane if it is perpendicular to two lines in the plane passing through their point of intersection.
.
Through each point of the plane you can draw a straight line perpendicular to it, and only one. All lines perpendicular to a given plane are parallel .
A perpendicular dropped from a given point onto a given plane is a segment connecting a given point with a point on the plane and lying on a straight line that is perpendicular to the plane. The base of a perpendicular is its end lying in a plane.
The distance from a point to a plane is the length of the perpendicular drawn from this point to the plane.
An inclined line drawn from a given point to a given plane is any segment connecting a given point with a point on the plane that is not perpendicular to the plane. The end of the segment that lies in the plane is the base of the inclined one . An oblique projection is a segment that connects the bases of a perpendicular (point C ) and an inclined one (point A ).
If a straight line drawn on a plane through the base of an inclined plane is perpendicular to its projection, then it is also perpendicular to the inclined one. And conversely, if a straight line in a plane is perpendicular to an inclined one, then it is also perpendicular to the projection of the inclined one .
Two intersecting planes are called perpendicular if the plane perpendicular to the line of their intersection intersects these planes along perpendicular lines.
Since, then.
Perpendicularity of lines in space
The purpose of the lesson:
Develop new knowledge and skills on the topic “Perpendicularity of a line and a plane”
Tasks:
— introduce the concept of perpendicular lines in space.
— prove the lemma about the perpendicularity of two parallel lines to a third line;
- define the perpendicularity of a straight line and a plane;
- prove theorems that establish the connection between the parallelism of lines and their
During the classes:
Organizing time.
Presentation in PowerPoint. Slide 1. Demonstration of statements on the slide.
Inspiration is needed in geometry no less than in poetry. (A.S. Pushkin)
The greatness of a person lies in his ability to think. (B. Pascal)
The task is not to teach mathematics, but to discipline the mind through mathematics. (V. Schrader)
– How do you understand quotes? Row task. Keeps track of time using a stopwatch.
Listens to the students' answers. If necessary, comments, clarifies, etc.
Slide 2. Lesson topic message
Slide 3. Communicating goals
Slide 4. Message of lesson objectives.
Updating knowledge
Slide 5. The teacher asks students 3 questions to repeat the material about the relative positions of straight lines and planes, studied in previous lessons (current control in the form of a frontal survey).
Studying new educational material.
Represents a cube model. Gives three tasks. He asks to make an assumption, find it in a geometry textbook (paragraph 15, p. 34). Informs that this is a lemma and follows a hyperlink to the interactive module (resource 1).
Scene 1. Modularly proves the lemma step by step with the help of students.
Scene 2.
Provides the definition of a line perpendicular to a plane. Asks to speak the definition orally, find it in the textbook.
Step-by-step proof of Theorem 1 and Theorem 2 using an interactive module based on student knowledge
Reinforcing educational material
Slide 6. Invites you to complete tasks in the interactive module. Comments on the task.
Scene 1.
Individual assistance.
Scene 2.
Individual assistance. Discussion of the result is collective.
Differentiated task for students. Four practical tests for the perpendicularity of lines and planes in space.
Help in reasoning, leading and clarifying questions.
Scene 1. Reproductive task.
Scene 2. Problem.
Scene 3. Problem of calculating the volume of a parallelepiped.
Scene 4. Problem of calculating the radius of a circle circumscribed about a triangle.
Homework assignment
Summing up the lesson
The entire summary - see the archive.