Перпендикулярность прямых и плоскостей Геометрия 10 класс Урок 1. — презентация
Перпендикулярность прямых и плоскостей Геометрия 10 класс Урок 1
План Перпендикулярные прямые в пространстве Перпендикулярные прямые в пространстве Определение прямой перпендикулярной к плоскости Определение прямой перпендикулярной к плоскости Параллельные прямые, перпендикулярные плоскости Параллельные прямые, перпендикулярные плоскости Признак перпендикулярности прямой и плоскости Признак перпендикулярности прямой и плоскости
Домашнее задание: Учебник пункты 15 – 17 Учебник пункты 15 – 17 ( п 16 без доказательств) ( п 16 без доказательств) 117, , 128
Вспомни Взаимное расположение прямых в пространстве Взаимное расположение прямых в пространстве Определение параллельных прямых Определение параллельных прямых Взаимное расположение прямой и плоскости Взаимное расположение прямой и плоскости Признак // прямой и плоскости Признак // прямой и плоскости
Вспомни Равнобедренный треугольник и его свойства Равнобедренный треугольник и его свойства Серединный перпендикуляр. Серединный перпендикуляр. Свойства точек серединного перпендикуляра Свойства точек серединного перпендикуляра А В
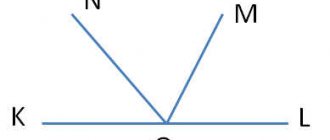
Перпендикулярные прямые Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90
Подумай Каким может быть взаимное расположение перпендикулярных прямых? Каким может быть взаимное расположение перпендикулярных прямых? Перпендикулярные прямые могут быть либо пересекающимися либо скрещивающимися. Приведи примеры
Задача А В С D D 1 С 1 А 1 Угол ВАD = 90 Докажите, что DC B1 C1 АВ А1D1
Л е м м а Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой. ДАНО: а // в, а с ДАНО: а // в, а с Доказать: в с Доказать: в с
Доказательство ДАНО: а // в, а с Доказать: в с Доказательство: а в с в//а, а // А М, поэтому в// М А Итак в//М А, с // М С, угол А М С = 90, значит угол между в и с = 90, т.е. в с
Задача А В С D D 1 С 1 А 1 Угол ВАD = 90 Докажите, что DC B1 C1 АВ А1D1
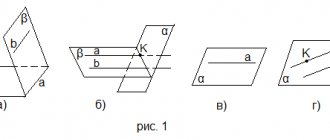
Прямые перпендикулярные к плоскости ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕНИЕ Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой лежащей в этой плоскости Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой лежащей в этой плоскости а β β
ПОДУМАЙ Каким может быть взаимное расположение прямой и плоскости, если они перпендикулярны? Каким может быть взаимное расположение прямой и плоскости, если они перпендикулярны? Приведи примеры из окружающей обстановки, иллюстрирующие перпендикулярность прямой и плоскости
Верно ли? Если прямая а перпендикулярна плоскости, то она перпендикулярна прямой АВ, лежащей в плоскости Если прямая а перпендикулярна плоскости β, то она перпендикулярна прямой АВ, лежащей в плоскости β
Задача Точки А, М, О лежат на прямой, перпендикулярной к плоскости Точки А, М, О лежат на прямой, перпендикулярной к плоскости β, а точки О, В, С и Д лежат в плоскости β. Сделай чертеж Какие из следующих углов являются прямыми: АОВ, МОС, ДАМ, ДОА, ВМО?
Связь между // прямых и их перпендикулярностью к плоскости. Теорема Если одна из двух // прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости Если одна из двух // прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости
Связь между // прямых и их перпендикулярностью к плоскости. Теорема Если две прямые перпендикулярны плоскости, то они параллельны. Если две прямые перпендикулярны плоскости, то они параллельны. Сделай чертеж
Признак перпендикулярности прямой и плоскости Теорема Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости а
а О Р q m ДАНО: а р, а q? ДОКАЗАТЬ: а β β а L
p q L a A B P Q L
p q L a A B P Q L О
Задача Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника МВД, где Д – лежит на прямой АС А В С М Д
Итак.. Прямая называется перпендикулярной к плоскости, если… Если две прямые перпендикулярны к плоскости, то они … Если одна из двух параллельных прямых перпендикулярна плоскости, то …
Верно ли? Если прямая а параллельна плоскости, а прямая в перпендикулярна к этой плоскости, то прямые а и в взаимно перпендикулярны?
Параллельность и перпендикулярность прямых и плоскостей в пространстве
Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.
Две плоскости называются параллельными, если они не пересекаются.
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.
, так как
Отрезки параллельных прямых между параллельными плоскостями равны.
= =
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.
Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.
.
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.
Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).
Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.
Так как , то .
Перпендикулярность прямых в пространстве
Цель урока:
Сформировать новые знания и умения по теме «Перпендикулярность прямой и плоскости»
Задачи:
— ввести понятие перпендикулярных прямых в пространстве.
— доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой;
— дать определение перпендикулярности прямой и плоскости;
— доказать теоремы, в которых устанавливается связь между параллельностью прямых и их
Ход урока:
Организационный момент.
Презентация в программе PowerPoint. Слайд 1. Демонстрация высказываний на слайде.
Вдохновение нужно в геометрии не меньше, чем в поэзии. (А.С. Пушкин)
Величие человека — в его способности мыслить. (Б. Паскаль)
Задача заключается не в том, чтобы учить математике, а в том, чтобы при посредстве математике дисциплинировать ум. (В.Шрадер)
– Как вы понимаете цитаты? Задание по рядам. Засекает время по секундомеру.
Слушает ответы обучающихся. При необходимости комментирует, уточняет и т.п.
Слайд 2. Сообщение темы урока
Слайд 3. Сообщение целей
Слайд 4. Сообщение задач урока.
Актуализация знаний
Слайд 5. Учитель задает 3 вопроса учащимся на повторение материала о взаимном расположении прямых и плоскостей, изученном на предыдущих уроках (текущий контроль в форме фронтального опроса).
Изучение нового учебного материала.
Представляет модель куба. Дает три задания. Просит выдвинуть предположение, найти в учебнике геометрии (п. 15, с.34). Сообщает, что это лемма, по гиперссылке выходит на интерактивный модуль (ресурс 1).
Сцена 1. По модулю поэтапно осуществляет доказательство леммы с помощью учащихся.
Сцена 2.
Предъявляет определение перпендикулярной прямой к плоскости. Просит проговорить определение устно, найти в учебнике.
Доказательство поэтапное теоремы 1 и теоремы 2 по интерактивному модулю с опорой на знания учащихся
Закрепление учебного материала
Слайд 6. Предлагает выполнить задания по интерактивному модулю. Комментирует задание.
Сцена 1.
Индивидуальная помощь.
Сцена 2.
Индивидуальная помощь. Обсуждение результата коллективное.
Дифференцированное задание ученикам. Четыре практических задания-теста на перпендикулярность прямых и плоскостей в пространстве.
Помощь в рассуждениях, наводящие и уточняющие вопросы.
Сцена 1. Репродуктивное задание.
Сцена 2. Задача.
Сцена 3. Задача на вычисление объема параллелепипеда.
Сцена 4. Задача на вычисление радиуса окружности, описанной около треугольника.
Задание на дом
Подведение итогов занятия
Весь конспект — смотрите архив.