Basic properties of multiplication
Since the action of multiplication is a special case of the action of addition, the basic properties of addition also apply to multiplication.
The action of multiplication, like addition, can always be performed, and in this case the only result of this action is obtained.
Laws of multiplication and their consequences
Multiplication has the following basic properties, called the laws of multiplication, from which other properties and consequences follow:
- commutative law of multiplication;
- combinational law of multiplication.
Commutative law of multiplication . The product of two or more factors does not change when their order is changed. This means that the value of the product does not depend on the order of multiplication of the factors, that is, on the order in which the multiplication action is performed.
For two factors, we can write the commutative multiplication law in general form as follows:
ab =ba .
Let's say we need to count the number of compartments in the closet (Fig. 1).
Picture 1.
5 of them in the top row 5 in the middle and bottom rows. It is not difficult to calculate that there are a total of them in all rows: 5+5+5=15 , or 5 ∙3=15 .
But these same compartments can also be counted vertically, in columns: in the first there are 3 , in the second there are also 3 , in the third, fourth and fifth columns there are also 3 of them. That is, there are 3 sections in each column. 5 columns in total , so: 3+3+3+3+3=15 , or 3 ∙5=15 .
It means that 5 ∙3=3 ∙5.
This property is also true for three or more factors.
For example, we need to count the number of compartments in two identical cabinets (Fig. 2).
Figure 2.
In the first cabinet, the number of compartments, as we have already found out, can be found by multiplying the number of compartments in one row by the number of rows: 5 ∙3.
In the second cabinet, the number of compartments is exactly the same ( 5 ∙ 3 ), since the two cabinets are completely identical.
The total number of compartments in two cabinets can be found by adding the number of compartments in each cabinet: 5 ∙3+5 ∙3.
The expression 5 ∙3 is nothing more than a repeated term, so we can replace this sum with a product by multiplying the term 5 ∙3 by the number of its repetitions, that is, by 2 :
5 ∙3+5 ∙3 =5 ∙3 ∙2.
Having found the results of the left and right sides of this equality, we will be convinced that they are the same, which means that we have replaced the sum with the product correctly:
15+15=15 ∙2,
30=30.
But we can also find the number of compartments in one cabinet by multiplying the number of rows by the number of compartments in one row: 3 ∙ 5 . Then in two cabinets we will have:
3 ∙5+3 ∙5=3 ∙5 ∙2,
15+15=15 ∙2,
30=30.
Means, 5 ∙3 ∙2=3 ∙5 ∙2=30.
We can also immediately multiply the number of cabinets by the number of compartments in one cabinet. Then we get: 2 ∙5 ∙3=30 or 2 ∙3 ∙5=30 , depending on how we calculated how many compartments one cabinet contains.
Therefore, for three factors, the commutative multiplication law in general looks like this:
abc=acb=bac=bca=cab=cba.
Combinative law of multiplication . The result of multiplying three or more numbers does not change if any of these factors are replaced by their product. Therefore, we can group the factors together in any way we want, and perform the multiplication operation with these groups.
In general form, for three factors, the combination law of multiplication can be expressed as follows:
abc=a(bc)=(ab)c=b(ac).
This law can be called a consequence of the commutative law of multiplication.
Indeed, according to the commutative law, we can transfer the factors at the end of the expression a ∙ b ∙ c ∙ d to its beginning and combine them into one group ( c ∙ d ) ∙ a ∙ b , that is, find their product c ∙ d . And since when the order of the factors is changed, the result of the multiplication action does not change, then changing the order of the groups of factors of one product also does not affect the result.
So, when calculating the number of compartments in two cabinets in Figure 2, we can first find the number of compartments in one cabinet, and then multiply the result by 2:
(5 ∙3) ∙2=15 ∙2=30,
or
(3 ∙5) ∙2=15 ∙2=30,
But we can first find the total number of rows of compartments in both cabinets, and then multiply them by the number of compartments in the row:
(3 ∙2) ∙5=6 ∙5=30.
As you can see, the result is the same in all cases.
Special cases of multiplication: multiplying one and zero
If in the product of two numbers one of the factors is one , then the product is equal to the second factor:
a ∙1=1 ∙a=a.
Indeed, when multiplying any number by 1 , we take this number 1 time, which means we get only this number.
And when multiplying one by any number (for example, 1 ∙ 7 ) we find the sum of seven units, that is, the number of units that make up this number. Therefore, the sum of these units is equal to the given number itself:
1+1+1+1+1+1+1=7.
If in the product of any number of factors one of the factors is zero , then the product is equal to zero:
a ∙ b ∙ 0=0 ∙ a ∙ b =a ∙ 0 ∙ c =0.
So, when multiplying any number by 0 , we take this number 0 times, that is, we don’t take it even once. And if you don’t take anything, then nothing will happen.
And when we multiply zero by any number, we find the sum of zeros, which, as you know, is equal to 0.
Division
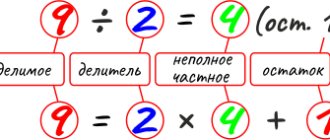
The action by which the product and one of the factors is used to find another factor is called division.
They write, 48:12=4.
The number that is divided by (48) is called divisible. The number by which (12) is divided is called the divisor. The result of division (4) is called quotient.
Name the dividend and divisor in quotients:
1.(254 + 781) : (97 - 92); (254 + 781) – dividend, (97 – 92) – divisor
2. 18c: a; 18c – dividend, a – divisor
3. (3 - y) : m; (3 - y) – dividend, m – divisor
4. x : (b + 5); x – dividend, (b + 5) – divisor
When dividing natural numbers, you can use the following properties:
1. a : 0 !!!
No number can be divided by zero.
2. a : 1 = a
When you divide a number by one you get the same number.
3. a : a = 1, a
When dividing a number by the same number, if it is not equal to zero, the result is one.
4. 0 : a = 0, a
When zero is divided by any number, if it is not equal to zero, the result is zero.
For example, 0 : 27 = 0; 85 : 1 = 85; 87:87 = 1.
Multiplying single digit numbers
Multiplying two single-valued natural numbers a and b is finding the sum of b terms, each of which is equal to the number a , and at the same time a and b are natural numbers.
If a and b are numbers located at the very beginning of the natural series, then finding such a sum is not difficult: 1 ∙2=1+1=2 . But if we take the numbers that close the first ten, for example, 8 and 9 , then to calculate 8 ∙9 , namely, the sum 8+8+8+8+8+8+8+8+8=72 , then in this In this case, calculating the result will require us some time.
To facilitate the calculation, the results of multiplying all single-digit numbers by each other were calculated and compiled into special multiplication tables.
Multiplying single-digit numbers is the basis for quickly and accurately calculating the products of any numbers, so it is very important to know all the multiplication tables by heart.
Multiplying a multi-digit number by a single-digit number
Let's say we need to multiply 985 by 4 . Multiplying 985 by 4 is adding 985 4 times , that is, 985+985+985+985 . We can represent each of the terms of 985 as the sum of its digit terms, namely: 900+80+5 . You will get the following expression:
900+80+5+900+80+5+900+80+5+900+80+5.
Let's use the laws of addition and group the same terms of this expression together:
900+900+900+900+80+80+80+80+5+5+5+5,
(900+900+900+900)+(80+80+80+80)+(5+5+5+5).
We can replace the sums in brackets with the product of identical terms and the number of these terms in each bracket:
900 ∙4+80 ∙4+5 ∙4.
Thus, to multiply a multi-digit number by a single-digit number , it is enough to multiply this single-digit number by the number of units in each digit of the multi-digit number, and add the results.
Column multiplication of a multi-digit number by a single-digit number
It’s convenient and quick to multiply a multi-digit number by a single-digit number, and writing the calculation in a column helps you avoid getting confused in the calculation.
To do this, we write the multiplicand 985 , and under the digit of its units place we write the factor 4 . We draw a horizontal line under the factor, put a multiplication sign (a dot or a diagonal cross) between the factors, and we get the following notation:
4 times 5 units - this will be 20 units, that is, 2 tens and 0 simple units. Therefore, we write 0 , and 2 tens or write a small number 2 above the tens place of the multiplicand 985 :
4 times 8 tens is 32 tens. Let's add to them 2 tens, which were obtained after multiplying a single-digit number by ones, we get 32 tens, that is, 3 hundreds and 2 tens. the number 2 under the line in the tens place, and above the hundreds place of the multiplicand 975 (in our head) we put a small number 3 :
4 times 9 hundreds is 36 hundreds. Let's add to them 3 hundreds, which we keep in mind, we get 39 hundreds, or 3 thousand and 9 hundreds. 9 under the horizontal line in the hundreds place and, since there is not a single thousand in the multiplicand 985 3 in the thousands place under the line as a result
How to explain division with a remainder?
Sometimes it is impossible to divide into equal shares. The easiest way to explain this situation to a student is to use a simple problem. For example:
There are 8 students in the group, and for lunch they were given 18 cheesecakes on a tray. When everyone receives 2 cheesecakes (18:8 = 2 and the rest is 2), there will be an extra 2 pieces left on the tray. This is the remainder.
The solution in a column with a remainder, according to the mathematical rule, is written in exactly the same way as without it. The only difference is that there will be a remainder at the end. In this option, it is correct to write down the number of whole units and the number of units in the remainder (example: 4 whole units and 9 in the remainder).
A student’s learning should take place in stages, from simple examples to more complex ones. If you do not understand the simple operations in division, then you need to repeat the information again. Gradually, solving examples will begin to happen faster and more confidently. The main thing is to believe in the strength of the little person, be patient, and then dividing numbers using the column method will become an interesting activity for the student.
Multiplying multi-digit numbers
Before I tell you how to generally multiply one multi-digit number by another, I will talk about two special cases of multiplying multi-digit numbers:
- multiplication by a number that starts with one and ends with any number of zeros;
- multiplication by a number that begins with any non-zero digits and ends with one or more zeros.
Multiplication by a number consisting of one and any number of zeros
Let it be necessary to multiply 327 by 10 . This means that we must take (add) the number 327 10 . It is known that if we take (add) one unit 10 times, then we get 1 ten, which means that by taking 327 units 10 times, we will have 327 tens, that is, 3270 units. Means:
327 ∙10 =3270
Let's look at another example. Let's multiply 327 by 100 , that is, take (add) the number 327 100 . If a unit is repeated 100 times, the result is 100 units, or one hundred. This means that 327 units repeated 100 times will give us 327 hundreds, which can be written like this: 32700 .
327 ∙100 =32700
So, to multiply any number by another that begins with one and ends with any number of zeros , it is enough to add as many zeros to the end of the first number as are contained in the second number.
Multiply by a number that begins with digits and ends with any number of zeros
For example, let's multiply the same number 327 , but by 20 . This means that we must add the same number 327 to each other 20 times:
327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327.
Let's use the associative law of multiplication and imagine these terms in the form of 10 identical groups, each of which contains two terms 327 :
(327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327).
We can, according to the definition of the action of multiplication, replace the sum in brackets with a product, since the summands of the sums are the same. We get the following:
(327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2).
But here again we see that the expression consists of ten identical terms, each of which represents a product. This means that we can represent this expression as a product:
(327 ∙2) ∙10.
Let's look at another example: 764 ∙300.
Here we need to find the sum of 300 numbers, each of which is the number 764 . We group these 300 100 groups, each of which contains 3 terms 764 . Can we find out how many units each of the 100 groups contains? Yes we can. To do this, we need to find the sum of three terms 764 , or simply 764 multiplied by 3 .
764 ∙3 =2292.
Knowing how many units are in one group and the number of these identical groups, we can find how many units are in all these groups. We have 100 , which means we find the sum of 100 terms, each of which is the number we found 2292 . That is, 2292 by 100 . To do this, simply add two zeros 2292
2292 ∙100 =229200.
So, to multiply any number by another, starting with any digits and ending with zeros , it is enough to multiply the first number by the number formed by the first digits of the second, and to the result add as many zeros to the right as there were at the end of the second number. In other words: you need to discard the ending zeros from the second number, multiply the resulting numbers, and add to the result as many zeros on the right as were originally discarded.
General rule for multiplying numbers
Let's say you need to find the product of two multi-digit numbers 2834 and 168 . This means that we need to add 168 identical numbers, each of which is equal to 2834 :
We can decompose the number of terms ( 168 100+60+8 ) and, according to the combinational law of addition, group them as follows: one hundred terms plus sixty terms plus eight terms.
Based on the definition of multiplication, we can present the expressions in brackets not as a sum of a large number of terms, but as a sum of products:
Thus, to multiply two multi-digit numbers , it is enough to sequentially multiply one of these numbers by the number of units of each of the digits of the second number, and add the results.
A quotient product is a number obtained after multiplying one of the factors by the number of units of any digit of the other factor.
Column multiplication of multi-digit numbers
When writing the multiplication action in a column, the factors are located one below the other in such a way that the corresponding digits of both numbers coincide; We draw a horizontal line under the factor and put a multiplication action sign between the factors:
Next, we multiply the multiplicand 2834 sequentially by the number of units of each digit of the multiplier from right to left, that is, starting from the least significant digit.
We multiply 2834 by 8 units, we get 22672 units. The result of the multiplication, that is, the first quotient product, is written under the horizontal line.
Next, we need to multiply the multiplicand by 6 tens; To do this, we multiply 2834 by 6 , and add 0 , we get 170040 .
In private works, they usually do not write (omit) zeros at the end of the number to simplify the notation. At the same time, we should not forget that the first digit of the partial product obtained must be written in the digit whose digit we are multiplying by the multiplicand.
In our case it looks like this. The number 6 , which we multiply by the multiplicand 2834 , is in the number 168 in the tens place, that is, it indicates the number of tens. Consequently, the first digit of the partial product obtained must be written in the tens place, because now we are multiplying the number of tens by the multiplicand.
So, 6 ∙4 =24 , which means we write in the line under the first partial product in the tens place the number 4 , and 20 tens, that is, 2 hundreds. Then we count and write in the same way as any other multiplication of multi-digit and single-digit numbers. After finding the second partial product, we got the following record:
Now we multiply the multiplicand by 1 hundred. To do this, just multiply 2834 by 1 and add two zeros to the right, you get 283400 . But we don’t write zeros in the entry, so we start writing the third particular work from the hundreds place.
All we have to do is add up the three resulting partial products.
So, the result of multiplication 2834 ∙168 = 476112.
Some features of writing multiplication in a column
When writing the product of two numbers in a column, there are some features that help shorten the recording and simplify the clarity of the calculation. All of them are a consequence of the properties of multiplication.
If the first factor has less digits than the second, then it is convenient to swap the factors when writing in a column, writing the number with more digits first. For example, the product 284 ∙12093 is found as 12093 ∙284 . This is done to eliminate the need to find many private works.
If some numbers in the multiplier are zeros, then you don’t have to write down the corresponding intermediate products, which, obviously, will also equal zero. In this case, the intermediate product obtained from multiplying the next significant digit (that is, non-zero) by the multiplicand begins to be written from the digit corresponding to the position of this significant digit. For example:
If one of the factors is a number that ends in any number of zeros, then we write the factors in a column as if these zeros were not there, find the product by mentally discarding these zeros, and then add the discarded zeros to the number obtained after multiplication and get the final result .
If both factors are numbers ending in any number of zeros, then we write them in a column as if these zeros did not exist, and after finding the product of numbers without zeros, we assign to them as many zeros as there were originally.
Try to prove the validity of this statement yourself. Write in the comments whether it worked for you or not.
Changing the product of numbers when changing its factors
To understand what happens to the product of numbers when one or more factors change, you need to remember that the action of multiplication is a special case of the action of addition, as well as the commutative and associative laws of addition.
If you increase one of the factors several times, the product will also increase by the same number of times.
Let's look at the example 18 ∙2 . By increasing the second factor, for example, by 3 times, we get another expression: 18 ∙6 .
Really:
18 ∙2 =36 18 ∙6 =108.
If we increase 36 by 3 times, then we get exactly 108 .
It can’t be any other way, and here’s why.
The first product is the sum of two terms:
18+18.
The second product is the sum of six identical terms:
18+18+18+18+18+18.
If we, using the associative law of multiplication, group these terms by 2 , we get the following:
(18+18)+(18+18)+(18+18).
As you can see, we have 3 identical terms, each of which is equal to the first product. This means that the resulting product consists of three that were given initially, that is, 3 times more than the initial one. Q.E.D.
For the second factor, the validity of this property is proved on the basis of the commutative law of multiplication.
If you decrease one of the factors several times, the product will also decrease by the same number of times.
Try to prove the correctness of this property yourself. Write in the comments, did it work out for you?
If you increase one of the factors several times, and decrease the second one by the same number of times , then the product will not change.
Indeed, when one of the factors increases, the product increases, and when the other factor decreases, the product decreases. Therefore, if you increase one number and simultaneously decrease another number, then these changes will compensate each other, and the product will remain unchanged:
32 ∙8 =256,
Let's increase the first factor by 4 times, and reduce the second by the same amount:
128 ∙2 =256.
Now let’s reduce the first factor of the product 32 ∙8 by 4 times, and the second factor by the same number of times:
8 ∙32 =256.
Multiplying a product by a number and numbers by a product
If you need to multiply a product by a number , you need to multiply any factor of this product by a given number, and multiply the result sequentially by the remaining factors. (a ∙b ∙c) ∙d =(a ∙d) ∙b ∙c =(b ∙d) ∙a ∙c =(c ∙d) ∙a ∙b
Indeed, let us want to find the result (7 ∙9 ∙2) ∙5 . We can first calculate the product in parentheses (it is 126 ), and then multiply it by 5 (the result is 630 ). Or we can, to quickly calculate the result in our heads, first multiply 5 by 2 to get the round number 10 , and then easily calculate two more products using the particular multiplication rules described above:
10 ∙7 =70 (we simply add a zero to seven), 70 ∙9 =630 7 ∙9 =63 from the multiplication table and add a zero to the end).
That is, we see that (7 ∙9 ∙2) ∙5 = (5 ∙2) ∙7 ∙9.
When I write “find from the multiplication table,” this means that we remember this row from the table, and do not actually look for it there. You need to know the multiplication table by heart!
If you need to multiply a number by a product , you need to multiply this number by any factor, and multiply the result by the remaining factors. a ∙(b ∙c ∙d) =(a ∙b) ∙c ∙d =(a ∙c) ∙b ∙d =(a ∙d) ∙b ∙c.
Consider this example: 6 ∙(3 ∙5 ∙2) . If you find the value of the product in parentheses ( 30 ) and then multiply the number 6 , the result will be 180 . Or you can first multiply the number 6 by 5 (it will be 30 ), and then multiply the result with the other factors:
30 ∙3 =90,
90 ∙2 =180.
Both of these properties are obvious consequences of the commutative and associative laws of multiplication.
Multiplication principle
The multiplication operation implies an action that replaces repeated addition. One of the arguments is called the multiplicand, and the other the multiplier. The result of multiplication is a product. Finding it is quite simple if you know the properties of the operation.
Sufficient rules, knowing which one can find the product of any numbers, include:
- Conjunctive - if you change the order of the arguments when multiplying a product by any number, the result will not change. In literal form, the law looks like: a * b * c = a * c * b. This rule can be proven experimentally. If you take squares of size 1 by 1 and build a block of 6 by 6 from them, then in fact it will be a multiplication of 1 * 6 = 6. The resulting rectangle can be combined with similar 3. That is, 3 * 1 = 3. The total number of squares will be 1 * 6 * 3 = 18. If the assembly sequence is changed, first assemble an item from three blocks, and then add 6 to them, the result will not change.
- Distributive - when performing an operation on a sum and a number, you can separately multiply each member of the expression by a factor, and then add the results. In mathematical notation, the rule looks like this: a * (b + c) = a * b + a * c. Another operation is called opening parentheses. This rule is similar for subtraction. But there is a nuance that the multiplication is performed first by the minuend, and then by the subtracted, and the second is subtracted from the first.
- Multiplication by 0. Any natural number when multiplied by 0 will give an answer of 0. The converse is also true.
For multiplication up to 100, there is a special table that you need to know by heart.
It should also be understood that when the number increases tens of times, the answer will increase by the number of zeros in the multiplied digit. For example, 34 * 10 = 340; 980 * 1000 = 980000. Thus, arbitrarily complex multiplication is performed for numbers greater than ten.
The product is often found using the column method . The essence of the method is that the arguments are written one after another. In this case, the rightmost digit of the upper number should be above the rightmost digit of the lower one. Next, perform bitwise multiplication starting with the lowest terms. If a higher digit is formed in this case, it is added to what is being multiplied.
The result of multiplying the next ten is shifted one to the left. Next, add up the results obtained and get the desired product.