Задачи по теме «Площадь» 8 класс
Задачи по теме «Площадь»
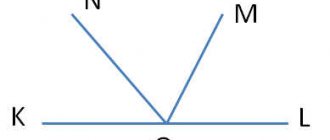
1.Найдите площадь треугольника, изображённого на рисунке.
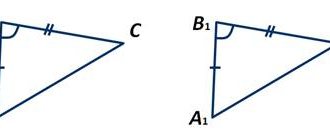
2. Найдите площадь треугольника, изображённого на рисунке.
3. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
4. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
5. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.
6.В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45∘. Найдите площадь треугольника.
7. Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
8. В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45∘. Найдите площадь треугольника.
9. Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
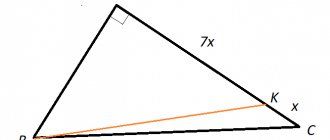
10. Найти площадь фигуры
. Найдите площадь треугольника, изображённого на рисунке
11. В прямоугольном треугольнике гипотенуза равна 4, а один из острых углов равен 45∘. Найдите площадь треугольника.
12. В прямоугольном треугольнике гипотенуза равна 8, а один из острых углов равен 45∘. Найдите площадь треугольника.
13.Боковая сторона равнобедренного треугольника равна 15, а основание равно 18. Найдите площадь этого треугольника.
14. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
15.
16. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
17. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
18. Найдите площадь параллелограмма, изображённого на рисунке.
19. В треугольнике со сторонами 18 и 9 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
20. Площадь параллелограмма ABCD
равна 6. Точка
E
– середина стороны
AB
. Найдите площадь трапеции
EBCD
.
21. Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
22. В треугольнике со сторонами 8 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
23. В треугольнике со сторонами 2 и 10 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 5. Чему равна высота, проведённая ко второй стороне?
24. Периметр равнобедренного треугольника равен 162, а основание — 72. Найдите площадь треугольника.
25. В треугольнике со сторонами 15 и 5 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
26. Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
27. Площадь параллелограмма ABCD
равна 56. Точка
E
— середина стороны
CD
. Найдите площадь трапеции
AECB
.
28. Найти площадь фигуры
29. Найти площадь фигуры
30. Найти площадь фигуры
31. В трапеции ABCD
AD
=3,
BC
=1, а её площадь равна 12. Найдите площадь треугольника
ABC
.
32.
33. Найти площадь фигуры
34. Найти площадь фигуры
35. Найти площадь фигуры
36. Высота BH
ромба
ABCD
делит его сторону
AD
на отрезки
AH
=5 и
HD
=8. Найдите площадь ромба.
37. Найти площадь фигуры
38. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
39. Найти площадь фигуры
40. Найдите площадь ромба, если его диагонали равны 14 и 6.
41. В прямоугольном треугольнике один из катетов равен 17, а острый угол, прилежащий к нему, равен 45∘. Найдите площадь треугольника.
42. Найдите площадь квадрата, если его диагональ равна 1.
43. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
44. Площадь параллелограмма ABCD
равна 176. Точка
E
— середина стороны
AD
. Найдите площадь трапеции
AECB
.
45.
46. Периметр равнобедренного треугольника равен 288, а основание — 128. Найдите площадь треугольника.
47. Периметр равнобедренного треугольника равен 200, а основание — 96. Найдите площадь треугольника.
48.Найти площадь трапеции
Ответы:
Геометрия 8 класс «Решение задач по теме Площадь»
Кто из вас может объяснить нам как ее решать?
Давайте решим еще несколько заданий из открытого банка ФИПИ.
Такие задачи были внесены в главный труд древнегреческого математика Эвклида, учебник «Начала», люди в течении двух тысячелетий изучали геометрию по этому учебнику.
Значит мы могли бы с вами учиться и в школе Евклид
Оцените свою работу на бланке самооценки
Еще один известный древнегреческий философ и геометр Пифагор. А чем знаменит Пифагор?
Сформулируйте и запишите теорему Пифагора на доске и в тетради. Как найти по теореме гипотенузу, как найти неизвестный катет?
Решите задачи на применение теоремы Пифагора.
А еще Пифагор был чемпионом античных Олимпийских игр.
Давайте и мы с вами немного разомнемся
Пифагор организовал свой Пифагорейский орден и Школу философов, и математиков. Туда принимали с большими церемониями и после долгих испытаний. В школе была очень серьезная дисциплина, существовали строгие правила –заповеди. Давайте узнаем какие?
Решите верно задачи и составьте текст заповедей. Учитель (ученики по рядам) раздает карточки с заданиями. Учитель инструктирует.
Карточка I.
№1. Катеты прямоугольного треугольника равны 3 и 4 см. Вычислите его гипотенузу.
| №2. Диагональ прямоугольника ABCD — 10 см. Сторона АВ = 8 см. Вычислите сторону ВС. | |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 5 – не гоняйся за счастьем | 4 – оно присутствует около тебя |
| 6 – не бегай за счастьем | 6 – оно всегда находится в тебе самом |
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
Карточка II.
| №1. Вычислите катет прямоугольного треугольника, если другой катет равен 8, а гипотенуза 10 см. | №2. Стороны прямоугольника равны 12 см и 5 см. Вычислите длину диагонали. |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 4 – формулы | 13 – управляют миром |
| 6 – числа | 14 – правят всем |
Ответ: Числа управляют миром.
Карточки для III
| №1.Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. | №2. Найти боковую сторону равнобедренного треугольника, если основание равно 8см, а высота, опущенная на основание — 3см. |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 8 – либо молчи | 5 – либо говори то, что ценнее молчания |
| 64 – хочешь-молчи | 6 – или говори о том, что интересно всем |
Ответ: Либо молчи, либо говори то, что ценнее молчания.
После выполнения, поднимите по рядам, какие же заповеди были в Пифагорейской школе? (Прикрепить на доску)
Заполните бланк самооценки, максимальный балл -3
Часто встречаются задачи, в которых необходимо доказать, что треугольник прямоугольный. Знание какой теоремы нам пригодится в этом случае?
Давайте вспомним обратную теорему Пифагора
Назовите тройки чисел подтверждающие это утверждение.
Составьте на бланках три Пифагоровы тройки
После ответов учеников вывести слайд
Пифагор был не только великим геометром, но и философом древности, он считал, что «Числа правят миром». Вы согласны с этим высказыванием? Не числа правят миром, а мы с их помощью решаем множество практических задач, таких например, как эта
—
Вычислите стоимость ламината, который нужно уложить в комнате длиной 5,5 м и шириной 4.5 м, если одна доска 20 см×130 см. Стоимость одной дощечки 156 руб.
| Длина комнаты в см | Ширина комнаты в см | Площадь пола комнаты в см2 | ||
| 550 | 450 | |||
| Длина дощечки в см | Ширина дощечки в см | Площадь одной дощечки в см2 | Количество дощечек | Стоимость всего ламината в руб. |
| 130 | 20 |
Самостоятельная работа по геометрии в 8 классе по теме «Площади фигур»
1 вариант
1. Сторона параллелограмма равна 21см, а высота, проведенная к ней 15см. Найдите площадь параллелограмма.
2,Стона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 6 и 10см,а высота равна полусумме длин оснований. Найдите площадь трапеции
2 вариант
1. Сторона параллелограмма равна 17см, а его площадь187 см². Найдите высоту, проведенную к данной стороне.
2.Сторона треугольника равна18см, а высота, проведенная к ней , в 3 раза меньше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 4 и 12см,а высота равна полусумме длин оснований. Найдите площадь трапеции.
1 вариант
1. Сторона параллелограмма равна 21см, а высота, проведенная к ней 15см. Найдите площадь параллелограмма.
2,Стона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 6 и 10см,а высота равна полусумме длин оснований. Найдите площадь трапеции
2 вариант
1. Сторона параллелограмма равна 17см, а его площадь187 см². Найдите высоту, проведенную к данной стороне.
2.Сторона треугольника равна18см, а высота, проведенная к ней, в 3 раза меньше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 4 и 12см,а высота равна полусумме длин оснований. Найдите площадь трапеции.
1 вариант
1. Сторона параллелограмма равна 21см, а высота, проведенная к ней 15см. Найдите площадь параллелограмма.
2,Стона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 6 и 10см,а высота равна полусумме длин оснований. Найдите площадь трапеции
2 вариант
1. Сторона параллелограмма равна 17см, а его площадь187 см². Найдите высоту, проведенную к данной стороне.
2.Сторона треугольника равна18см, а высота, проведенная к ней , в 3 раза меньше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 4 и 12см,а высота равна полусумме длин оснований. Найдите площадь трапеции.
1 вариант
1. Сторона параллелограмма равна 21см, а высота, проведенная к ней 15см. Найдите площадь параллелограмма.
2,Стона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 6 и 10см,а высота равна полусумме длин оснований. Найдите площадь трапеции
2 вариант
1. Сторона параллелограмма равна 17см, а его площадь187 см². Найдите высоту, проведенную к данной стороне.
Все формулы по геометрии. Площади фигур
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .