Тесты по геометрии для 10 класса (стр. 1 )

Контрольные работы по геометрии в 10 классе

ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ ПО ГЕОМЕТРИИ В 10 КЛАССЕ

Диагностическая контрольная работа

Тестовая контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение двух прямых в пространстве»

Контрольная работа по теме «Параллельность прямых и плоскостей в пространстве»

Семестровая контрольная работа

Контрольная работа по теме «Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная»

Контрольная работа по теме «Теорема о трех перпендикулярах. Перпендикулярность плоскостей»

Контрольная работа по теме «Координаты в пространстве»

Контрольная работа по теме «Векторы в пространстве»

ПО по теме «Координаты и векторы в пространстве»

Итоговая контрольная работа»

Диагностическая контрольная работа

Вариант-1

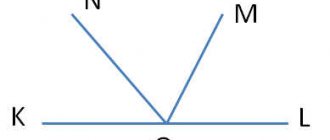
Из точки М к прямой а
проведены перпендикуляр МВ и наклонные МА и МС. Найдите длину перпендикуляра, если наклонные МА=41
см,
МВ=50
см,
а их проекции на данную прямую относятся как 3:10.

В прямоугольном треугольнике из вершины прямого угла к гипотенузе проведены медиана и высота, расстояние между основаниями которых равно 14 см.
Найдите периметр треугольника, если его гипотенуза равна 100
см.
Читайте также: Цветы из фоамирана презентация к уроку (подготовительная группа)

Стороны параллелограмма равны 6 см
и 7
см,
а сумма его диагоналей равна 18
см
. Вычислите диагонали параллелограмма.

Диагностическая контрольная работа

Вариант-2

Из точки М к прямой а
проведены перпендикуляр МВ и наклонные МА и МС. Найдите длину перпендикуляра, если длины наклонных относятся как 10:17, а их проекции на данную прямую равны 12
см
и 30
см
.

В треугольнике сторона равна 6 см
, один из углов, прилежащих к этой стороне, равен , сторона, лежащая против этого угла, равна 28
см
. Найдите площадь треугольника.

Диагонали параллелограмма равны 12 см
и 14
см
, а разность сторон равна 4
см
. Вычислите периметр параллелограмма.

Тематическая контрольная работа

по теме «Параллельность прямых и плоскостей в пространстве»

Вариант-1

Изобразите куб ABCDABCD. Точки K, L, M – середины ребер АВ, AD, AA соответственно.

а) Запишите ребра куба, параллельные грани ABCD.

б) Каково взаимное расположение прямой KL и плоскости BDC?

в) Каково взаимное расположение плоскостей KLM и BDA ?

Сторона АВ треугольника АВС лежит в плоскости , а вершина С не лежит в этой плоскости. Точки M и N – середины сторон АС и ВС соответственно. Докажите, что прямая MN параллельна плоскости .

Отрезок АВ не пересекает плоскость , С – середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость в точках А, В, С соответственно. Найдите АА, если ВВ= 4 см, СС= 3 см.

Тематическая контрольная работа

по теме «Параллельность прямых и плоскостей в пространстве»

Вариант-2

Изобразите куб ABCDABCD. Точки K, L, M – середины ребер АВ, AD, AA соответственно.

а) Запишите грани куба, параллельные ребру AА.

б) Каково взаимное расположение прямой ML и плоскости ADС?

в) Каково взаимное расположение плоскостей KLM и BDС ?

Основание АD трапеции АВСD лежит в плоскости , а точки В и С не принадлежат этой плоскости. Докажите, что прямая ВС параллельна

плоскости .

Плоскость пересекает стороны АВ и АС треугольника АВС в точках В и С соответственно, ВС // . Найдите АС, если АС= 2 см,

ВС : ВС=2

Семестровая контрольная работа

Вариант-1

Прямая имеет с плоскостью треугольника одну общую точку. Будет ли эта прямая принадлежать плоскости треугольника?

Плоскости и параллельны. Сторона АВ треугольника АВС принадлежит плоскости , плоскость пересекает сторону АС в точке А, а сторону ВС в точке В. При этом АВ:АВ=5:4. Отрезок АА=18 см. Найти АС.

Плоскости и параллельны. Прямая АВ лежит в плоскости , а прямая CD — в плоскости , при этом АВ не параллельна CD. Будут ли прямые АС и BD параллельны?

Семестровая контрольная работа

Вариант-2

Прямая пересекает смежные стороны ромба. Будет ли эта прямая принадлежать плоскости ромба?

Отрезок АВ не пересекает плоскость . Через концы отрезка и его середину проведены параллельные прямые, пересекающие плоскость в точках А, М, В. Найти длину отрезка АА, если ММ=5 см, а ВВ=7 см.

Вне плоскости треугольника АВС лежит точка S. На отрезках

AS, BS, CS отмечены соответственно точки M, N, K так, что

АМ:MS=BN:NS=CK:KS=2:1. Доказать, что плоскости MNK и

АВС параллельны.

Тематическая контрольная работа

по теме «Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная»

Вариант-1

Изобразите куб АВСDABCD. Пользуясь изображением куба, запишите ребра куба, перпендикулярные ребру АА и пересекающие его.
Из точки А к плоскости проведена наклонная АВ . Найти длину проекции этой наклонной на плоскость , если АВ=26 см, а точка А удалена от плоскости на 10 см.
Из точки А, взятой вне плоскости , проведены к ней две наклонные, длины которых равны 10 и 17 см.Разность проекций этих наклонных на плоскость равна 9 см. Найдите проекции наклонных.
Расстояние от точки М до всех вершин квадрата равно

10 см. Найдите расстояние от точки М до плоскости

квадрата, если диагональ квадрата равна 12 см.

Тематическая контрольная работа

по теме «Перпендикулярность прямой и плоскости.

Перпендикуляр и наклонная»

Вариант-2

Изобразите прямоугольный параллелепипед АВСDABCD. Пользуясь его изображением, запишите грани параллелепипеда, перпендикулярные ребру АА.
Из точки М к плоскости проведена наклонная МN. Найти длину наклонной , если длина её проекции на плоскость равна 8 см, а точка М удалена от плоскости на 6 см.
Из точки А, взятой вне плоскости , проведены к ней две наклонные. Найдите длины наклонных, если одна из них на

13 см больше другой, а проекции наклонных на плоскость

равны 6 и 20 см.

Расстояния от точки S до всех вершин правильного треугольника равны по 5 см, а до плоскости треугольника —

3 см. Найдите высоту треугольника.

Тематическая контрольная работа

по теме «Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная»

Вариант-3

Изобразите куб АВСDABCD. Пользуясь изображением куба, запишите ребра куба, перпендикулярные грани АВСD
Из точки А к плоскости проведена наклонная АВ . Найти расстояние от точки А до плоскости , если АВ=17 см, а длина проекции АВ на плоскость равна 8 см.
Из точки А, взятой вне плоскости , проведены к ней две наклонные, длины проекций которых равны 2 и 14 см, а наклонные относятся как 1:2. Найдите длины наклонных.
Расстояния от точки М до всех вершин квадрата равны по

13 см, а до плоскости квадрата – 12 см. Найдите диагональ квадрата.

Тематическая контрольная работа

по теме «Перпендикулярность прямой и плоскости.

Перпендикуляр и наклонная»

Вариант-4

Изобразите прямоугольный параллелепипед АВСDABCD. Пользуясь его изображением, запишите ребра параллелепипеда, перпендикулярные ребру DC и пересекающие его .
Из точки М к плоскости проведена наклонная МN. Найти длину проекции этой наклонной на плоскость , если

МN =20 см, а точка М удалена от плоскости на 12 см.

Из точки А, взятой вне плоскости , проведены к ней две наклонные, проекции которых равны 8 и 20 см. Найдите длины наклонных, если известно, что их разность равна 8 см.
Расстояние от точки S до каждой вершины правильного треугольника равно 10 см. Найдите расстояние от точки S до плоскости треугольника, если медиана треугольника равна 9 см.

Тематическая контрольная работа

по теме «Теорема о трех перпендикулярах.

Перпендикулярность плоскостей»

Вариант-1

Через вершину С квадрата ABCD проведена прямая МС, которая перпендикулярна плоскости квадрата.

1) Докажите, что прямые ВD м МО перпендикулярны, где

О – точка пересечения диагоналей.

2) Вычислите расстояние от точки М до прямой ВD, если

МС = 1 см, СD = 4 см.

Концы отрезка, длина которого равна см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояния от концов этого отрезка до линии пересечения плоскостей равны 5 см и 8 см. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
Через вершину D прямоугольника АВСD к его плоскости проведен перпендикуляр DЕ. Точка Е удалена от стороны АВ на 10 см, а от стороны ВС – на 17 см. Найдите длину диагонали ВD, если ЕD = 8 см.

Тематическая контрольная работа

по теме «Теорема о трех перпендикулярах.

Перпендикулярность плоскостей»

Вариант-2

Через вершину А равностороннего треугольника АВС проведена прямая DА, которая перпендикулярна плоскости треугольника, М – середина стороны ВС.

1) Докажите, что прямые ВС и МD перпендикулярны.

2) Вычислите расстояние от точки D до прямой ВС, если

АD = 4 см, АВ = 6 см.

Концы отрезка, длина которого равна см, принадлежат двум взаимно перпендикулярным плоскостям. Расстояния от концов этого отрезка до линии пересечения плоскостей равны 6 см и 7 см. Найдите расстояние между основаниями перпендикуляров, опущенных из концов отрезка на линию пересечения плоскостей.
Через вершину С ромба АВСD к его плоскости проведен перпендикуляр СF. Точка F удалена от диагонали ВD на 25 см. Найдите расстояние от точки F до плоскости ромба, если

ВD = 20 см, АВ = см.

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 1.

Даны точки А(1;0;-2), В(-2;1;3) и вектор (1;0;-2).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты суммы векторов и .

Найдите длину вектора 2+3, если (3;1;0), (0;1;-1).
Найдите косинус С треугольника АВС, если А(0;1;-1),

В(1;-1;2), С(3;1;0).

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 2.

. Даны точки А(3;2;1), В(1;2;3) и вектор (1;1;1).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты разности векторов и .

. Найдите длину вектора -3+2, если (3;-2;-1), (1;2;-4).

Найдите косинус А треугольника АВС, если А(0;1;-1),

В(1;-1;2), С(3;1;0).

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 3.

Даны точки С(1;0;1), D(1;1;2) и вектор (1;2;3).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты вектора 2.

Найдите длину вектора 2+3, если (1;1;-1), (2;0;0).

. Найдите величину В треугольника АВС, если А(2;2;-4),

В(2;-1;-1), С(3;-1;-2).

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 4.

. Даны точки М(1;0;2), К(1;1;2) и вектор (1;-1;0).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты вектора 3.

. Найдите длину вектора -2+3, если (2;-1;3), (-1;2;5).

. Найдите величину А треугольника АВС, если А(2;-2;-3)

В(4;-2;-1), С(2;2;1).

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 5.

. Даны точки К(1;0;-2), Р(-2;1;3) и вектор (1;0;-2).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты разности векторов и .

. Найдите длину вектора -2 + 3, если (3;1;0), (0;1;-1;).

. Найдите косинус С треугольника АВС, если А(0;1;-1),

В(1;-1;2), С(3;1;0).

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

Вариант – 6.

. Даны точки M(1;2;3), N(3;2;1) и вектор (2;3;1).Найдите:

а) координаты вектора ;

б) абсолютную величину вектора ;

в) координаты суммы векторов и .

Найдите длину вектора 3- 2, если (2;0;-3), (1;-2;-1).

Найдите косинус А треугольника АВС, если А(0;1;-1),

В(1;-1;2), С(3;1;0).

ПО по теме

«Координаты и векторы в пространстве».

Вариант – 1

Даны три вершины А(1;-2;3), В(2;3;-5), D(-4;5;1) параллелограмма ABCD. Найти координаты его четвертой вершины С.
Найти на оси у
точку, равноудаленную от точек А(-3;7;4) и В(2;-5;1).
Даны точки М(3;-2; 2), N(2;-1;0), К(-1;-5;4) и Р(0;-4;4). Найти угол между векторами и .
Даны векторы и такие, что =4, =
3, а угол между векторами и равен 120 . Найти 3+2 .

ПО по теме

«Координаты и векторы в пространстве».

Вариант –2

. Даны три вершины А(2;-8;9), В(-1;3;4), С(-4;6;3)

параллелограмма ABCD. Найти координаты его четвертой

вершины D.

Найти на оси
х
точку, равноудаленную от точек М(-2;6;3) и

Р(4;-3;5).

Даны точки А(1; 3; 3), В(1;0;2), С(-1;-1;3) и D(-1;0;3).

Найти угол между векторами и .

Даны векторы и такие, что =3, =
2, а угол между векторами и равен 60 . Найти 2-3 .

Итоговая контрольная работа

по геометрии в 10 классе.

Вариант – 1.

В треугольнике АВС С=90, АС=9 см, ВС=12 см,

М-середина ВА. Прямая КС перпендикулярна плоскости АВС, КС=18 см. Найти КМ.

Из вершины прямого угла С треугольника АВС к его плоскости проведен перпендикуляр СК. Расстояние от точки К до прямой АВ равно 13 см. Найти расстояние от точки К до плоскости треугольника, если его катеты равны 15 см и 20 см.

1) Найти координаты точки М- середины отрезка АВ, если А(-2;3;4), В(6;1;-2). 2)Найти длину вектора .

3) Найти скалярное произведение векторов и .

Итоговая контрольная работа

по геометрии в 10 классе.

Вариант – 2.

Из вершины А правильного треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Найти расстояние от точки К до вершин треугольника, если ВС= см, КВА=30 .

Из вершины угла С треугольника АВС к его плоскости проведен перпендикуляр СК. Расстояние от точки К до прямой АВ равно 26 см. Найти расстояние от точки К до плоскости треугольника, если АС=30 см, АВ=28 см,

ВС=26 см.

1) Найти координаты точки М- середины отрезка АВ, если А(-3;0;4), В(3;5;-2). 2)Найти длину вектора .

3) Найти скалярное произведение векторов и.

Г10(I)-1. Параллельность прямых, прямой и плоскости

Геометрия. 10 класс. Глава I. Тест 1.

Вариант 1.

1. Выбрать верное утверждение.

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна этой плоскости.

4) Через любую точку пространства проходит прямая, параллельная данной прямой, и притом только одна.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки E, F, P и K –середины отрезков АС, АМ, ВМ и ВС. Найти периметр четырёхугольника EFPK,

если МС=21 см, АВ=13 см.

A) 8 см; B) 34 см; C) 17 см; D) 68 см.

4. Сторона АС треугольника АВС лежит в плоскости α. МϵАВ, NϵBC, MN||α, причём BM:AM=2:7, MN=6 см. Сделать чертёж. Найти АС.

A) 18 см; B) 30 см; C) 27 см; D) 36 см.

Вариант 2.

1. Выбрать верное утверждение.

1) Если плоскость проходит через прямую, параллельную другой плоскости, то эти плоскости будут параллельны.

2) Если две прямые параллельны третьей прямой, то они перпендикулярны.

3) Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.

4) Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

A) 1; B) 4; C) 3; D) 2.

2. Какой из чертежей на рисунке 1 может служить иллюстрацией следующего утверждения: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна?

A) б); B) а); C) в); D) г).

3. На рисунке 2 точки F, P, Q и N –середины отрезков АB, АМ, CМ и ВС. Найти периметр четырёхугольника FPQN, если AС=17 см, ВM=25 см.

A) 32 см; B) 21 см; C) 42 см; D) 84 см.

4. Плоскость α параллельна стороне АС треугольника АВС и пересекает стороны АВ и ВС в точках К и F соответственно, BF:FC=5:6, АС=22 см. Сделать чертёж. Найти KF.

A) 15 см; B) 9 см; C) 10 см; D) 12 см.

Вариант 3.

1. Выбрать верные утверждения.

1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2) Если параллельные прямые а и b лежат в плоскости α, то и прямая с, пересекающая прямые а и b, лежит в плоскости α.

3) Если средняя линия трапеции лежит в плоскости α, то прямые, содержащие её основания пересекут плоскость α.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Возможны три случая взаимного расположения прямой и плоскости: а) прямая и плоскость имеют только одну общую точку; б) прямая лежит в плоскости; в) прямая и плоскость не имеют ни одной общей точки.

А) б); в); B) а); б); г); C) б); в); г); D) а).

3. На рисунке 2 точки E, F, P и K – середины отрезков АС, АМ, ВМ и ВС. Периметр четырёхугольника EFPK равен 32 см, причём разность длин любых его смежных сторон составляет 2 см. Найти МС и АВ (МС

A) MC=14 см; AB=18 см; B) MC=15 см; AB=17 см;

C) MC=12 см; AB=20 см; D) MC=10 см; AB=22 см.

4. Отрезок АВ пересекает плоскость α в точке О. Точка С – середина отрезка ОВ. Параллельные прямые, проведённые из точек А, В и С к плоскости α, пересекают её в точках А1, В1 и С1 соответственно. АА1=6 см, А1О:ОС1=1:3. Сделать чертёж. Найти ВВ1.

A) 18 см; B) 30 см; C) 32 см; D) 36 см.

Вариант 4.

1. Выбрать верные утверждения.

1) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

2) Возможны три случая взаимного расположения прямой и плоскости: а) прямая лежит в плоскости; б) прямая и плоскость пересекаются; в) прямая и плоскость параллельны.

3) Если стороны MN и NP параллелограмма MNPQ пересекают плоскость α, то и прямые MQ и PQ пересекут эту плоскость.

A) 1); 2); 3); B) 1); 3); C) 1); 2); D) 2); 3).

2. Каким чертежом (какими чертежами) на рисунке 1 можно проиллюстрировать следующее утверждение.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

А) б); в); B) а); C) а); б); D) а); г).

3. На рисунке 2 точки F, P, Q и N – середины отрезков АB, АМ, CМ и ВС. Периметр четырёхугольника FPQN равен 38 см, причём разность длин любых его смежных сторон составляет 3 см. Найти AС и BM (AС

A) AC=14 см; BM=24 см; B) AC=16 см; BM=26 см;

C) AC=16 см; BM=19 см; D) AC=16 см; BM=22 см.

4. Отрезок АВ пересекает плоскость α в точке О. Точка С – середина отрезка ОВ. Параллельные прямые, проведённые из точек А, В и С к плоскости α, пересекают её в точках А1, В1 и С1 соответственно, АО:ОС=5:3, ВВ1=24 см. Сделать чертёж. Найти АА1.

A) 20 см; B) 24 см; C) 12 см; D) 10 см.

Справочные материалы.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Если две прямые параллельны третьей прямой, то они параллельны.

Возможны три случая взаимного расположения прямой и плоскости в пространстве: а) прямая лежит в плоскости; б) прямая и плоскость имеют только одну общую точку, т. е. пересекаются; в) прямая и плоскость не имеют ни одной общей точки.

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Метки: Геометрия 10 класс, параллельность прямых и плоскостей, прямая и плоскость

Ваш комментарий Отменить ответ

Практическое занятие. Тема: Перпендикуляр и наклонная.

Практическое занятие

Тема:
Перпендикуляр и наклонная.
Цели:

Образовательная:

продолжить формирование у студентов умений решать задачи по теме «Перпендикуляр и наклонная».

Воспитательная:

воспитание самостоятельности, творческого подхода к решению задач.

Развивающая:

развитие логического мышления, навыков сравнительного анализа.

Оборудование:

доска, компьютер, проектор, экран, индивидуальные карточки-задания, записи на доске.

Использование элементов педагогических технологий:

1. сотрудничества;

2. здоровье сберегающих (чередование видов деятельности);

3. информационно-коммуникационных;

4. развивающих;

5. личностно-ориентированных.

Результативность:

формирование компетенций: ценностно-смысловой, учебно-познавательной, коммуникативной, личного самосовершенствования.

План занятия.

1) Подготовительный этап.

Повторение опорных знаний.

1) Проверка усвоения пройденного материала фронтально (или индивидуально) по следующим вопросам (на экран проектируются вопросы, на которые студенты отвечают устно).

1. Дайте определение прямой, перпендикулярной плоскости.

2. Какая прямая называется наклонной к плоскости?

3. Что называется проекцией наклонной на плоскость?

4. Как формулируется теорема о трех перпендикулярах?

5.Как определяется угол между прямой и плоскостью?

2) Теоретический этап.

а) К плоскости α проведена наклонная, длина которой равна 13 см, проекция наклонной равна 5 см. На каком расстоянии от плоскости находится точка, из которой проведена наклонная?

б) Расстояние от точки D до каждой из вершин правильного треугольника ABC равно 15 см. Найдите расстояние от точки D до плоскости ABC, если АВ = 10 см.

3) Практический этап.

Самостоятельное применение умений и знаний.

Провести самостоятельную работу в 15 вариантах. (Приложение 1)

Список литературы.

1. Алимов Ш.А. и др.

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.

2. Богомолов Н.В.

Математика: учебник для прикладного бакалавриата / Н.В. Богомолов, П.И. Самойленко. – 5-е изд., перераб. и доп. – М.: Издательство Юрайт, 2014.

Приложение 1.

Варианты для самостоятельной работы.

Вариант 1

1)Точка А не лежит в плоскости, а точка Е — принадлежит этой плоскости. АЕ = 13 cм, проекция этого отрезка на плоскость равна 5см. Каково расстояние от точки А до данной плоскости?

2)Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны по 10 см, а сторона основания AE=16 см. К этой плоскости проведены перпендикуляр CB, который равен 6 см, и наклонные CA и CE. Вычислите расстояние от точки C до стороны треугольника AE.

3) Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD, перпендикулярная к плоскости треугольника, а) Докажите, что треугольник CBD прямоугольный, б) Найдите BD, если ВС = 4, DC =6.

Вариант 2

1) Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 30°. P∈a, точка R — проекция точки P на плоскость β. PR=7 см. Найди PC.

2)Прямоугольный треугольник MBE (∢M=90°) находится в плоскости α. BE=13 см, а ME=12 см. К этой плоскости проведён перпендикуляр CB длиной 7 см. Вычисли расстояние от точки C до стороны треугольника ME.

3)Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно, что АВ =АС = 5 см, ВС= 6 см, AD = 12 см. Найдите расстояния от концов отрезка AD до прямой ВС.

Вариант 3

1) К плоскости α проведена наклонная, длина которой равна 10 см, проекция наклонной равна 6 см. На каком расстоянии от плоскости находится точка, из которой проведена наклонная?

2) Точка K расположена в расстоянии 8 cm от плоскости прямоугольника ABCD и в равных расстояниях от вершин прямоугольника.

Рассчитай, на каком расстоянии от вершин прямоугольника расположена точка K, если длина сторон прямоугольника 24 cm и 18 cm.

3) Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что KD = 6 см, КВ = 7 см, КС=9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника ABCD;

Вариант 4

1) К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 18 см, наклонная с плоскостью образует угол 60°. Вычисли, на каком расстоянии от плоскости находится точка B.

2) Расстояние от точки G до каждой из вершин правильного треугольника ABC равно 12 см. Найдите расстояние от точки G до плоскости ABC, если АВ = 9 см.

3) Прямая ОК перпендикулярна к плоскости ромба ABCD, диагонали которого пересекаются в точке О. Найдите это расстояние, если ОК = 4,5 дм, АС = 6 дм, BD = 8 дм.

Вариант 5

1) Прямая m пересекает плоскость ß в точке A, и образует с плоскостью угол 60°,P∈ m, точка R — проекция точки P на плоскость β. PR=9 см. Найди PА.

2)Наклонная AD с плоскостью α образует угол 30˚, а наклонная DC с плоскостью α образует угол 45˚. Длина перпендикуляра DB равна 7 см. Вычисли длины обеих наклонных.

3) Через вершину В квадрата ABCD проведена прямая BМ, перпендикулярная к его плоскости. Найдите расстояния от точки М до прямых, содержащих стороны и диагонали квадрата, если BМ = 10 дм, АВ = 5 дм.

Вариант 6

1) Длина отрезка VB равна 10 м. Он пересекает плоскость в точке O. Расстояние от концов отрезка до плоскости соответственно равны 2 м и 3 м. Найди острый угол, который образует отрезок VB с плоскостью.

2) Один из катетов прямоугольного треугольника ABC равен 5, а острый угол, прилежащий к этому катету, равен 60˚. Через вершину прямого угла С проведена прямая CD, перпендикулярная к плоскости этого треугольника, CD = 8. Найдите расстояние от точки D до прямой АВ.

3) Из точки А, удаленной от плоскости ß на расстояние 5 см, проведены к этой плоскости наклонные АВ и АС под углом 30° к плоскости. Их проекции на плоскость ß образуют угол в 120°. Найдите ВС.

Вариант 7

1) Проекции наклонных AD и DC на плоскости α равны соответственно 4 см и 10 см, а угол между ними равен 60°. Вычисли расстояние между концами проекций наклонных.

2) Точка M расположена в расстоянии 10 cm от плоскости прямоугольника ABCD и в равных расстояниях от вершин прямоугольника.

Рассчитай, на каком расстоянии от вершин прямоугольника расположена точка M, если длина сторон прямоугольника 12 cm и 5 cm.

3) Один конец данного отрезка лежит в плоскости α, а другой находится от нее на расстоянии 11 см. Найдите расстояние от середины данного отрезка до плоскости α.

Вариант 8

1) К плоскости α проведена наклонная СD (C∈α). Длина наклонной равна 16 см, наклонная с плоскостью образует угол 30°. Вычисли, на каком расстоянии от плоскости находится точка D.

2) Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если BF = 8 дм, АВ = 4 дм.

3) Отрезок КD перпендикулярен к плоскости равнобедренного треугольника КРЕ. Известно, что КР =КЕ = 4 см, РЕ= 8 см, КD = 14 см. Найдите расстояния от концов отрезка КD до прямой РЕ.

Вариант 9

1) Наклонная АМ, проведенная из точки А к данной плоскости, равна 7см. Чему равна проекция этой наклонной на плоскость, если угол между прямой АМ и данной плоскостью равен 30°?

2) Расстояние от точки N до каждой из вершин правильного треугольника ABC равно 5 см. Найдите расстояние от точки N до плоскости ABC, если АВ = 8 см.

3) Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что KD = 6 см, КВ = 7 см, КС=9 см. Найдите расстояние между прямыми АК и CD.

Вариант 10

1) Наклонная АМ, проведенная из точки А к данной плоскости, равна 15. Чему равна проекция этой наклонной на плоскость, если угол между прямой АМ и данной плоскостью равен 60°.

2) Прямая BD перпендикулярна к плоскости треугольника ABC. Известно, что BD = 9 см, АС=10 см, ВС = ВА = 13 см. Найдите расстояние от точки D до прямой AC

3) Точка М расположена в расстоянии 10 см. от плоскости прямоугольника ABCD и в равных расстояниях от вершин прямоугольника.

Рассчитай, на каком расстоянии от верши прямоугольника расположена точка M, если длина сторон прямоугольника 16 см и 10 см.

Вариант 11

1) Под углом φ к плоскости α проведена наклонная. Найдите φ, если известно, что проекция наклонной вдвое меньше самой наклонной.

2) Через вершину прямого угла С равнобедренного прямоугольного треугольника ABC проведена прямая СМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямой АВ, если АС = 4 см, а СМ = 2 √7 см.

3) Прямая BD перпендикулярна к плоскости треугольника ABC. Известно, что BD = 9 см, АС=10 см, ВС = ВА = 13 см. Найдите площадь треугольника ACD.

Вариант12

1) Проекции наклонных AМ и МC на плоскость α равны соответственно 5 см и 8 см, а угол между ними равен 45°.

Вычисли расстояние между концами проекций наклонных

2) Прямая ОК перпендикулярна к плоскости ромба ABCD, диагонали которого пересекаются в точке О. Докажите, что расстояния от точки К до всех прямых, содержащих стороны ромба, равны

3) Через вершину М квадрата MNOR проведена прямая MF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если MF = 12 дм, MN = 6 дм.

Вариант 13

1) Один конец данного отрезка лежит в плоскости ß, а другой находится от нее на расстоянии 12 см. Найдите расстояние от середины данного отрезка до плоскости ß.

2) Точка P расположена в расстоянии 12 см от плоскости прямоугольника ABCD и в равных расстояниях от вершин прямоугольника.

Рассчитай, на каком расстоянии от вершин прямоугольника расположена точка P, если длина сторон прямоугольника 8 см и 6 см.

3) Проекции наклонных MN и MK на плоскости α равны соответственно 8 см и 12 см, а угол между ними равен 30°. Вычисли расстояние между концами проекций наклонных.

Вариант 14

1) Наклонная АМ, проведенная из точки А к данной плоскости, равна 8см. Чему равна проекция этой наклонной на плоскость, если угол между прямой АМ и данной плоскостью равен 45°.

2) Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. Найдите расстояния от точки М до прямых, содержащих стороны ромба, если AB = 25 см, ∠BAD = 60°, BM =12,5 см.

3) Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АО и две наклонные АВ и АС. Известно, что ∠OAB= ∠BAС = 60°, АО = 1,5 см. Найдите расстояние между основаниями наклонных.

Вариант 15

1) Концы отрезка отстоят от плоскости α на расстояниях 3 см и 7 см. Найдите расстояние от середины отрезка до плоскости α.

2) Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.

3) Наклонная НМ, проведенная из точки Н к данной плоскости, равна 9см. Чему равна проекция этой наклонной на плоскость, если угол между прямой НМ и данной плоскостью равен 45°?