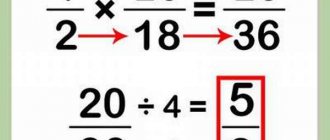Lesson plan:
On Saturday, 6th grade students agreed to meet and take a walk in the park. In the morning, Yulia looked out the window, the sun was shining brightly, but it was frosty. The girl looked at the thermometer. It showed -10˚C. Mom asked Yulia to go outside a little later, when it was warmer outside. Julia was upset and began to wait. Two hours later, the girl looked at the thermometer again. He showed -3. Wow! It’s only been two hours, but it’s gotten so warm – the girl was happy and began to get dressed to go for a walk. At this time, my mother entered the room and asked in surprise, “Is it warmer already? How many degrees? The daughter did not know what to say and how to correctly find out how many degrees it had become warmer. Mom came to the rescue and said that it is enough to subtract -3 from -10, and we will find out how many degrees the air temperature outside the window has changed. Otherwise, we can say that the thermometer scale has risen up by 7 divisions, which means that the street has become warmer by 7 degrees. Having remembered everything that her mother said, Yulia ran to the park to share her new knowledge with friends.
Adding and subtracting negative numbers
Let's remember the beloved fairy tale "Pinocchio" and look at the problem involving our favorite characters.
Life at the Karabas-Barabas Theater was very difficult for the actors; all the dolls dreamed of living in freedom. The actors worked hard, but the debts to the owner grew every day. The evil owner promised to release Pinocchio and Malvina from his theater only when the puppet heroes repaid their debt to him. How many coins do the heroes need to collect to be free, if Pinocchio had -15 coins and Malvina -6?
To answer the main question of the problem, we need to understand what we are talking about. Having studied the condition, the question arises: “How can there be -15 and -6 coins?” In this case, it turns out that Pinocchio and Malvina must return 15 and 6 coins to Karabas-Barabas, which is why there is a minus sign in front of these numbers. It turns out that the puppet characters will be able to leave the theater when the debt is fully repaid. To do this, you need to find out the total amount of debt of Pinocchio and Malvina. To find out the amount of debt, we add up the characters' coins -15 and -6. But how to add them when there is a “minus” in front of the terms? In such situations, the rule of adding negative numbers is applied.
Let's return to solving the problem.
Now, let’s correctly write and summarize the known data.
It turns out that the heroes have -21 coins, therefore, they must collect 21 coins and repay the debt, only then will it be possible to leave the Karabas-Barabas theater.
Let's look at one more task.
Find the result of adding -24 and -16.
To calculate the sum of two values with a minus sign, it is enough to sum their modules and write “-” in front of the resulting figure.
-24+(-16)=-(24+16)=-40.
Remember! If we add two negative numbers, then we sum their modules, and write “-” before the result of the addition.
Properties of divisors from 6 to 10
Composite six consists of the product of two consecutive numbers - 2 and 3. The theory of multiplicity is as follows: the number 6 is composite, therefore it is necessary that two rules for the sign of divisibility operate simultaneously. It is necessary that the number be a multiple of both two and three at once.
For example, three-digit numbers 756 and 168 are tested. They are even, so they are divisible by two. Now you need to add 7+5+6=18, it becomes clear that the sum of 18 is divisible by 3. The number 165, when decomposed into single digits and then added, turns into 12, which can be divided into three. Both numbers are multiples of both 2 and 3, which means they are multiples of six.
The definition of a ratio with divisibility by seven is quite complex: a number is divisible if, when the last digit is doubled and the resulting difference, the result is a multiple of seven or equal to zero.
Example, the three-digit number 679 is a multiple of 7. (The calculator returned 97). You can find out this way:
- 2*9=18.
- 67−18=49.
- 49:7=7.
The example shows that the last number was doubled, then the difference was obtained, after which the proof relation was obtained.
The class was given the task of proving that the number 497 is divisible by seven. Solution procedure:
- 2*7=14.
- 49−14=35.
- 35:7=5.
Finding the test for divisibility by 8 is very easy. The wording of the law is as follows: the last three digits must be 000 or 888. You can easily calculate with 789000: it is divisible by 8, since it ends in 000. The set 289673888 is also a multiple of 8, since it ends in 888.
The property of divisor 9 is similar to the rule with 3. The formula for divisibility by 9 is quite simple: the sum of the digits must be a multiple of nine. A small example: from 46980 it is possible to obtain an integer, 4+6+9+8+0= 27. The resulting sum is a multiple of 9. Another task: find the ratio using the factor of 9 when the dividend is 29565. Reasoning: 2+9+5+6 +5=27. The resulting amount can be divided by nine.
Adding numbers with different signs
Let's consider the situation.
Misha’s dad visited his grandmother in the village and promised to bring a gift for his son – apples. In the yard, Misha told the boys about daddy’s promise and decided to treat each of his three friends to an apple, that is, he already had -3 apples. Dad brought 10 apples to his son and the boy happily shared the fruit with his friends. How many apples does the boy have left?
To find the number of apples a boy has, we need to find out what the sum of apples is - those that the boy had (-3), and those that dad gave (10). That is, to answer the main question of the problem, it is enough to add -3 and 10. But the terms have different signs “+” and “-”. How to add positive and negative numbers? Once you remember the algorithm for adding positive and negative numbers, it will be very easy to do this.
We use the considered algorithm when performing actions.
Let's sum up 3 and 10. To do this:
- define the modules: -3=|3|, 10=|10|;
- we compare the modules, determining the larger one: |3|<|10|;
- subtract the smaller from the larger: 10 – 3=7;
- since by condition 10 is a positive number, then the result will be a positive number.
It is written in this form:
-3+10=10 – 3=7.
It turns out that the boy now has 7 apples.
Let's look at another example of adding numbers with different signs.
Calculate the sum of -28 and 11.
Known terms have different signs, that is, -28 is a negative value, and 11 is a positive value. To sum the terms, you need to use the previously discussed algorithm. First, we define the modules and compare them.
-28=|28|;
11=|11|;
28>11.
We remember that the negative term (-28) has a larger modulus value, so you will need to put a minus sign in front of the result. Now, we find the difference between the larger and smaller modulus values (28-17) and write the mathematical expression:
-28+11=-(28-11)=-17.
Considering the examples discussed, we can say that:
any numerical value always becomes larger when a positive number is added to it, and only smaller when a negative number is added.
Let's prove the validity of this rule by calculating the expression and comparing the minuend with the resulting sum: -150+50.
To find the value of the expression, you need to determine the modules (150 and 50), leaving the “-” sign for the module of the larger term, subtracting the smaller from the larger value:
-150+50=-(150-50)=-100.
Let's compare the found value of the expression (-100) with the one being reduced (-150), using the rule for comparing numbers with a negative sign:
When comparing digital values with a minus sign, the one whose modulus is greater will be smaller.
-150=|150|;
-100=|100|.
150>100;
-150<-100.
Indeed, when adding with a negative number, the minuend only became smaller.
Math lesson in 6th grade on the topic “Divisibility of numbers” algebra lesson plan (6th grade) on the topic
Lesson topic: Divisibility of numbers.
Lesson objectives:
1) educational: developing the ability to summarize the studied material, analyze, compare and draw conclusions;
2) educational: developing self-control skills; fostering a sense of responsibility;
3) developing: development of memory, imagination, thinking, attention, intelligence.
Equipment: examples written on the board for oral and independent work, worksheets, textbooks, projector, computer, screen.
Lesson type: combined.
During the classes.
- Organizing time.
- Updating knowledge.
Verbal counting.
- Name the divisors of the number 36. (Slide No. 2)
- Name several multiples of the number 36. (Slide No. 3)
- Which of the numbers 100, 250, 21, 47 are divisible by 10? (Slide No. 4)
- What numbers are divisible by 2? (Slide No. 5)
- What numbers are divisible by 5? (Slide No. 6)
- What numbers are divisible by 3? (Slide No. 7)
- What numbers are divisible by 9? (Slide no.

- What numbers are called prime? Composite? (Slide No. 9)
- Find GCD (12, 30). (Slide number 10)
- Find LOC (12, 30). (Slide No. 11)
- Consolidation, systematization, application of new knowledge and skills.
- Choose from the numbers 5, 7, 14, 23, 15, 33 those that are:
A) divisors of the number 60;
B) multiples of 7;
C) divisors of 20 and multiples of 5.
- Zhenya put 25 pencils into 2 boxes. Can the boxes contain the same number of pencils?
- Write down all the numbers consisting of the digits 1, 7, 0. Which of them are divisible by 10?
- Write down all two-digit numbers that are divisible by 5. Which ones are even? Which ones are divisible by 10?
- Write down all two-digit numbers ending in 3. Which ones are divisible by 3 and which ones are divisible by 9?
- Write down all two-digit numbers whose expansion consists of two simple single-digit numbers.
- The guys at the New Year's party received the same gifts. All the gifts together contained 27 oranges and 45 apples. How many children were at the party?
Solution. The solution to the problem is gcd (27, 45), which corresponds to the number of children. Let's factor 27 and 45 into prime factors: 45 = 3. 3. 5; 27 = 3. 3. 3. From here it is clear that GCD (27, 45) = 9. Therefore, there were 9 children at the holiday.
- Find LOC (108, 64).
Solution. 108 = 2. 2. 3. 3. 3; 64 = 2. 2. 2. 2. 2. 2. So LCM (108, 64) = 64. 27 = 1728.
- Testing knowledge and skills.
Independent work.
Compose two different even three-digit numbers that are divisible by 2, 5 and 9 and consist of the same digits. Find their gcd and lcd.
Solution. If the required numbers are divisible by 2, 5 and 9, then they are multiples of their product, i.e. 90. Let's make pairs:
180 and 810, gcd = 90, gcd = 1620;
270 and 720, gcd = 90, gcd = 1620;
360 and 630, gcd = 90, gcd = 2520;
450 and 540, GCD = 90, GCD = 2700.
Answer: 180 and 810, 270 and 720, 360 and 630, 450 and 540.
- Homework.
Inform students about homework, ensure they understand the content and how to complete it.
It is proposed to find GCD (a, b) and LCM (a, c). Take the numbers a and b yourself arbitrarily.
- Summing up the lesson.
Provide qualitative assessments of class and individual student performance.
Dear friends! To summarize the lesson, I would like to hear your opinion about the lesson.
What was interesting and instructive in the lesson?
Can I be sure that you can cope with tasks of this type?
Which tasks turned out to be the most difficult?
What knowledge gaps were revealed during the lesson?
What problems did this lesson create?
Teacher: Dear friends! Thank you very much for the pleasant communication. I thank everyone who took an active part in the work. You really helped me teach this lesson. I hope for further cooperation.
The lesson is over! (Slide No. 12).
Test on the topic: “Positive and negative numbers” for grade 6
Development of a mathematics lesson for 6th grade
Lesson No. 46 Date: 10/25/2020
Topic:
Test on the topic: “Positive and negative numbers.”
The purpose of the lesson:
Check the level of students’ knowledge on the topic: “Positive
and negative numbers. The absolute value of a number"
Tasks:
- To promote the development of skills in applying the rules for comparing rational numbers, solving equations and expressions with a modulus sign, and applying the coordinate line in practice.
- Develop memory, speech, observation, notice a pattern, generalize, make judgments by analogy, and the ability to work with a textbook.
- Develop logic of thinking and mental arithmetic speed.
- Cultivate accuracy when keeping notebooks and a responsible attitude towards learning.
- Arouse students' interest in studying mathematics, broaden their horizons; show that mathematics is a wonderful science.
Lesson structure
- Organizing time:
Distribute notebooks for tests, distribute work into two versions of two levels.
- Positive attitude.
To solve problems correctly, you need to think and reason. And, of course, calculate without errors. And this requires attention and effort.
- Main part:
Work solution:
1 option A
- Draw a coordinate line, taking the length of two notebook cells as a unit segment. a) Mark the points on it: A (-1), B (5) and C (-4).
b) Label with letters M, E and D the points whose coordinates are numbers,
opposite to the coordinates of points A, B and C.
- a) Write down all the integers that are located on the coordinate line between
numbers -5.1 and 7.3.
b) Between what integers on the coordinate line is the number -3.5 located?
Write your answer as a double inequality.
- Compare: a) -2 and 0; b) 3.14 and -5; c) -6 and -1.8; d) 1.25 and 0; e) and 7; e) and 4.
4. Solve the equations: = 6.7 b) = 8.2 c) -= 3.8
- Follow the steps: a) 48: + b) + ):;
6. Solve the problem by making a proportion: 56 dresses were sewn from 156.8 m of fabric. How many dresses
can it be sewn from 89.6 m of the same fabric?
2 options
- Draw a coordinate line, taking the length of two notebook cells as a unit segment. a) Mark the points on it: A (-2), B (3) and C (-5).
b) Designate with letters K, L and P the points whose coordinates are numbers,
opposite to the coordinates of points A, B and C.
- a) Write down all the integers that are located on the coordinate line between
numbers -4.8 and 8.5.
b) Between what integers on the coordinate line is the number -5,6 located?
Write your answer as a double inequality.
- Compare: a) -3 and 0; b) 2.15 and -6; c) -7 and -1.7; d) 1.25 and 0; e) and 6; e) and 9.
4. Solve the equations: = 12.4 b) = 3.8 c) -= 6.1
5. Follow these steps: a) 126: + b) ( — ):;
6. Solve the problem by making a proportion: For 5 kg of apples they paid 120 tenge. How much do you need
pay for 7 kg of apples?
Option 1 B
- Draw a coordinate line and mark point B (1) on it. Point D lies at a distance of 2 unit segments in the positive direction from point B, and point E lies at a distance of 3 unit segments in the negative direction from point B.
a) Write down the coordinates of points D and E;
b) Designate with letters K, L and P the points whose coordinates are numbers opposite
coordinates of points B, D and E.
- a) Write down all the integers that are located on the coordinate line between
numbers -6.2 and 6.7.
b) Between what integers on the coordinate line is the number -10.8 located?
Write your answer as a double inequality.
- Solve the equations: a) b) - c) ;
4. Compare: b) and ; c) -99 and 0.1; d) -8.7 and -8.6;
5. Follow these steps: ;
6. Solve the problem: The ratio of the boat’s own speed to the speed of the river current is
4:1. The speed of the river current is 6.9 km/h less than the boat's own speed. Which
How far will the boat travel in 2 hours along the river?
Option 2 B
- Draw a coordinate line and mark point A (-2) on it. Point B lies at a distance of 5 unit segments in the positive direction from point A, and point C lies at a distance of 2 unit segments in the negative direction from point A.
a) Write down the coordinates of points B and C;
b) Designate with letters K, L and P the points whose coordinates are numbers opposite
coordinates of points A, B and C.
- a) Write down all the integers that are located on the coordinate line between
numbers -8.3 and 4.3.
b) Between what integers on the coordinate line is the number -12.6 located?
Write your answer as a double inequality.
- Solve the equations: a) b) - c) ;
4. Compare: b) and ; c) -89 and 0.9; d) -7.8 and -7.6;
5. Follow these steps: ;
6. Solve the problem: Point C divides segment AB in the ratio 7:3. Find the length of segment AB,
if segment AC is 8 cm larger than segment CD.
- Setting homework: Make notes:
"Historical information about number systems and negative numbers."
- Summarizing. Reflection.