Subject of stereometry
We have been studying geometry for three years now and have almost always dealt with flat figures, that is, with figures that are entirely located in the same plane. The branch of geometry that deals with the study of the properties of plane figures is called planimetry. The main figures of planimetry are a point and a straight line.
Plane figures have only two dimensions: length and width, these measurements are used to find the area of the figures.
But let's look around. There are practically no flat bodies in nature. All objects are located in space and do not fit in one plane. The branch of geometry that studies the properties of such figures is called stereometry.
For example, if in planimetry we talked about a square, then in stereometry we will talk about a cube, which consists of squares.
If in planimetry we talked about a right triangle, then in stereometry from a triangle, rotating it around one of the legs, we get a cone.
The word stereometry comes from two ancient Greek words στερεός - “solid, spatial” and the word μετρέω - “measure”. Unlike planimetry, the main figures of stereometry are a point, a straight line and a plane.
Points, as in planimetry, are designated by capital letters of the Latin alphabet. Direct lines are designated by lowercase letters of the Latin alphabet.
A plane can be depicted in different ways, but most often it is depicted as a parallelogram. Lowercase letters of the Greek alphabet are used to designate a plane.
Along with these concepts, geometric bodies and their surfaces are considered in stereometry. Geometric solids have three dimensions: length, width and height.
These measurements make it possible to calculate the volume of the figure, that is, geometric bodies have capacity. Almost every object around us can be represented in the form of geometric bodies.
Bodies whose surfaces consist of polygons are called polyhedra.
Stereometry, like planimetry, arose and developed along with man. Geometry was very necessary for builders who erected dams on rivers, threw bridges and viaducts from one bank to another, and created multi-story buildings and majestic temples.
A striking example of this are the Egyptian pyramids, built two to four millennia BC. Until now, these pyramids amaze with the accuracy of their metric ratios.
Geometry is believed to have originated in ancient Egypt around 2000 BC. In the 5th century AD, the ancient Greek scientist Herodotus wrote about the emergence of geometry as follows: The Egyptian pharaoh Seozoostris divided the land, giving each Egyptian a plot by lot and levied a tax on each plot accordingly. It happened that the Nile flooded this or that plot, then the victim turned to the king, and the king sent surveyors to determine how much the plot had decreased and reduce the tax accordingly. This is how geometry arose in Egypt, and from there it moved to Greece.
Herodotus of Halicarnassus (
around 484 BC e. - around 425 BC e.)
At first, geometry was intuitive. That is, the facts were recognized as existing and were not proven in any way. But in the six hundredth year BC, the Greek scientist Thales put forward and developed the idea that there should be ways to prove the validity of certain facts. In geometry, facts are called theorems. Thales discovered proofs of theorems that people had taken for granted before.
Thales of Miletus
640/624 - 548/545 BC e.
Starting from the 7th century BC, philosophical schools were created in Ancient Greece, in which there was a gradual transition from practical to theoretical geometry.
One of the earliest and most famous geometric schools was the Pythagorean school, which existed in the sixth to fifth centuries BC. It was named in honor of its founder, the ancient Greek scientist Pythagoras.
Pythagoras of Samos
570 - 490 BC e.
The Pythagoreans used regular polyhedra for philosophical theories. So they gave fire the shape of a tetrahedron (pyramid), earth - the shape of a hexahedron (cube), air - the shape of an octahedron (a figure formed by eight equilateral triangles), water - the shape of an icosahedron (a figure formed by twenty equilateral triangles).
In their opinion, the entire universe has the shape of a dodecahedron (a figure that consists of twelve regular pentagons).
It is easy to notice that the names of polyhedra are also of ancient Greek origin. The first part of the name shows the number of faces the figure consists of, and the word hedron
comes from the ancient Greek word “edra” - edge.
Another famous school that dealt with issues of geometry is the Alexandrian philosophical school. A native of this school was the famous scientist Euclid, who lived around three hundred BC.
Euclid
OK. 325 - 265 BC e.
Euclid is the author of “Principia,” a work that consists of thirteen books and contains a presentation of planimetry, stereometry, and a number of issues in number theory. With this work, Euclid created the foundation for the further development of mathematics. Until now, this work is considered the basis for studying geometry.
He formulated 5 postulates:
1. You can draw a straight line through two points.
2. A straight line segment can be extended indefinitely.
3. From any center, a circle can be described by any distance.
4. All right angles are equal to each other.
5. And so that whenever a straight line, when intersecting with two other straight lines, forms internal one-sided angles with them, the sum of which is less than 2 straight lines, these straight lines intersect on the side on which this sum is less than 2 straight lines.
It is a widely known fact that King Ptolemy asked Euclid if it was possible to find a shorter and less tedious way to study geometry than his Elements. To which Euclid replied: “There is no royal path in geometry.”
In the 19th century, new methods appeared in geometry that made it possible to translate geometric problems into the language of algebra and vice versa. New directions of geometric research have emerged and are developing: Lobachevsky geometry, projective geometry, topology, computer geometry, and so on.
In 1829, Russian mathematician Nikolai Lobachevsky wrote the work “On the Principles of Geometry,” in which he stated that it was possible to construct a geometry as meaningful and free from contradictions as Euclidean. If Euclid’s geometry can be called the geometry of terrestrial spaces and distances, then Lobachevsky’s geometry is the geometry of giant interplanetary and vanishing small atomic spaces; it includes Euclid’s geometry as an integral part, as a special case.
Nikolai Ivanovich Lobachevsky
1792 – 1856
The main difference between Lobachevsky’s geometry and Euclid’s geometry is the so-called “fifth postulate”. Euclid stated that “ Through a point not lying on a given line there passes no more than one straight line that lies in the same plane with the given line and does not intersect it.”
.
In Lobachevsky's geometry, instead of this axiom, another axiom is accepted: Through a point not lying on a given line, there pass at least two lines that lie with a given line in the same plane and do not intersect it.
In 1899, the German mathematician David Hilbert wrote the work “Foundations of Geometry”. This work became a model for further work on the axiomatic construction of geometry.
David Gilbert
1862 – 1943
Geometric bodies, like all geometric figures, are imaginary objects. A geometric body is a part of space separated from the rest of space by the boundary of this body. In other words, we imagine geometric bodies as “empty”, that is, there is a shell, and inside we find empty space. For example, the boundary of a ball is a sphere. By analogy with planimetry, when a circle was the boundary of a circle. For each body, you can draw a plane, on both sides of which there will be points of this body. Such a plane is a secant plane.
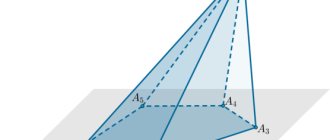
When studying spatial figures, use the image of these figures in the drawing. As a rule, the image of a spatial figure is its projection onto a particular plane. The same figure can be depicted in different ways. For example, a pyramid can be depicted like this:
Dashed lines represent invisible parts of the figure.
Usually, the image that creates the correct idea of the shape of the figure and is most convenient for studying its properties is chosen. Obviously, to depict the pyramid we will choose this drawing.
In 9th grade we will look at only a few geometric bodies. Such as prism, pyramid, cylinder, cone, sphere. In doing so, we will mainly rely on visual representations. We will study these bodies in more detail in geometry courses for grades 10 and 11.
Summary of a geometry lesson in 9th grade on the topic: Subject of stereometry. Polyhedron
Geometry lesson notes for 9th grade
Subject of stereometry.
Polyhedron. Author:
Pletnev Alexander Andreevich.
Place of work:
MBOU Komsomolskaya secondary school in Tyulpany village, Zavetinsky district, Rostov region
Teaching experience:
3 years
Objectives: to introduce students to a new section of geometry - stereometry, with geometric bodies and their surfaces;
consider various polyhedra and teach students to depict them. Lesson progress I Learning new material
Teacher: Hello, children! We will conduct today's lesson with you in the form of a lecture, but at some points you will help me. So far we have been studying which section of geometry? Children: Planimetry Teacher: That's right, we studied planimetry. Who can define planimetry? Children: Planimetry is a section of geometry that studies the properties of flat geometric figures, i.e. figures that are entirely located in a certain plane. Teacher: That's right, but if we look at the objects around us, are they flat? Children: No. Teacher: That's right, they are not flat, any object that surrounds us takes up some part of the space. Just in today’s lesson, we will get acquainted with a new section of geometry for you, which is called stereometry. Like almost all new concepts in mathematics, this word also has a Greek origin, “stereometry” comes from two Greek words: “stereo” - volumetric, spatial and “metreo” - to measure. In stereometry, the simplest figures are also considered, as in planimetry. Who can recall the simplest figures of planimetry? Children: point, line, plane. Teacher: Well done. In addition to the simplest figures that you have listed, geometric bodies and their surfaces are considered in stereometry. The objects around us give us ideas about geometric bodies. If we look at the surface of the crystal, we can notice that it consists of a number of polygons. In stereometry, such surfaces are called polyhedra. The simplest polyhedron is the cube.
Teacher: There are several important concepts inherent in polyhedra: • Vertex • Edge • Face • Diagonal Look at the picture and try to formulate the definition of face, edge and vertex. Children: Faces are the polygons that make up a polyhedron. Edges are the sides of faces. Vertices are the ends of edges. Teacher: That's right, guys! However, your definition of a face should be expanded, “faces are the polygons that make up a polyhedron, and no two adjacent faces lie in the same plane.” It remains for us to introduce the concept of diagonal. A diagonal is a segment connecting two vertices that do not belong to the same face. Now look carefully at the drawing and tell me how many faces, edges and vertices does the cube have? Children: 6 faces, 12 edges, 8 vertices Teacher: Correct.
A cube is not the only geometric body; in addition to it, there are many more bodies: a ball, a cylinder, a parallelepiped, a pyramid, a cone. cone parallelepiped pyramid cylinder ball (sphere) tetrahedron II.
Reinforcing the material learned Teacher: Guys, let's try to solve a crossword puzzle using the knowledge we gained today. Solve the crossword puzzle in pictures using the closest geometric bodies similar to a house as words. - 1
— 2 — 3 — 4 — 5 — 6
answers:
III Lesson summary.
Teacher: Guys, explain what a polyhedron is; what are the faces, edges, vertices and diagonals of a polyhedron. Give examples of polyhedra.
IV Homework assignment.
Teacher: homework: study paragraphs 118 and 119 of the textbook; solve task No. 1184.
We recommend watching:
Mathematics lesson on the topic Diagrams in the 6th grade Game “Field of Miracles” in mathematics for students of grades 5-6 of correctional schools of the VIII type Extra-curricular activity in mathematics for students of the correctional schools of the VIII type Summary of a mathematics lesson in the 5th grade “Journey to the Land of Mathematics”
Similar articles:
Game as a means of interactive learning in the subject Mathematics
Summary of a 6th grade math lesson on the topic: Multiplication and division of ordinary fractions
Extracurricular math activity for 7th-8th grade students. Game "Weak Link"
Summary of a 9th grade mathematics lesson on the topic: Arithmetic and geometric progressions
Summary of a 5th grade math lesson on the topic: Multiplication and division of decimals by natural numbers