Предмет стереометрии
Мы с вами геометрию изучаем уже третий год и практически постоянно имели дело с плоскими фигурами, то есть с фигурами, которые целиком расположены в одной плоскости. Раздел геометрии, который занимается изучением свойств плоских фигур называется планиметрия. Основными фигурами планиметрии являются точка и прямая.
У плоских фигур есть только два измерения: длина и ширина, эти измерения используются для нахождения площади фигур.
Но давайте посмотрим вокруг. В природе практически нет плоских тел. Все предметы располагаются в пространстве и не умещаются в одной плоскости. Раздел геометрии, который изучает свойства таких фигур, называется стереометрией.
Например, если в планиметрии мы говорили о квадрате, то в стереометрии мы будем говорить о кубе, который состоит из квадратов.
Если в планиметрии мы говорили о прямоугольном треугольнике, то в стереометрии из треугольника, вращая его вокруг одного из катетов, мы получим конус.
Слово стереометрия происходит от двух древне-греческих слов στερεός — «твёрый, пространственный» и слово μετρέω — «измеряю». В отличии от планиметрии основными фигурами стереометрии являются точка, прямая и плоскость.
Точки, как и в планиметрии обозначаются заглавными буквами латинского алфавита. Прямые обозначаются строчными буквами латинского алфавита.
Плоскость может изображаться разными способами, но чаще всего она изображается параллелограммом. Для обозначения плоскости используются строчные буквы греческого алфавита.
Наряду с этими понятиями в стереометрии рассматриваются геометрические тела и их поверхности. У геометрических тел три измерения: длина, ширина и высота.
Эти измерения позволяют вычислить объем фигуры, то есть геометрические тело обладают вместимостью. Практически каждый окружающий нас предмет можно представить в виде геометрических тел.
Тела, поверхность которых состоят из многоугольников называют многогранниками.
Стереометрия, как и планиметрия, возникла и развивалась вместе с человеком. Геометрия была очень нужна строителям, которые возводили на реках дамбы, перекидывали с одного берега на другой мосты, виадуки, создавали многоэтажные здания и величественные храмы.
Ярким примером этого являются египетские пирамиды, сооруженные за два четыре тысячелетия до нашей эры. До сих пор эти пирамиды поражают точностью своих метрических соотношений.
Считается, что геометрия появилась в древнем Египте около 2000 лет до нашей эры. В 5 веке нашей эры древнегреческий ученый Геродот о появлении геометрии писал так: Египетский фараон Сеозоострис разделил землю, дав каждому египтянину участок по жребию и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию.
Геродо́т Галикарна́сский (
около 484 г до н. э. — около 425 г до н. э.)
Сначала геометрия была интуитивной. То есть факты признавались существующими и никак не доказывались. Но в шестисотом году до нашей эры греческий ученый Фалес выдвинул и развил идею о том, что должны быть пути, доказывающие справедливость тех или иных фактов. В геометрии факты называются теоремами. Фалес открыл доказательства теорем, которые люди принимали на веру до этого.
Фалес Милетский
640/624 — 548/545 гг. до н. э.
Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к теоретической геометрии.
Одной из самых первых и самых известных геометрических школ была пифагорейская, она существовала в шестом пятом веках до нашей эры. Названа она была в честь своего основателя древнегреческого ученого Пифагора.
Пифагор Самосский
570 — 490 гг. до н. э.
Пифагорейцы использовали правильные многогранники для философских теорий. Так огню они придавали форму тэтраэдра (пирамиды), земле – форму гексаэдра (куба), воздуху – форму октаэдра (фигуры, которая образована восьмью равносторонними треугольниками), воде – форму икосаэдра (фигуры, которая образована двадцатью равносторонними треугольниками).
По их мнению вся вселенная имеет форму додекаэдра (фигуры, которая состоит из двенадцати правильных пятиугольников).
Нетрудно заметить, что названия многогранников тоже имеют древнегреческое происхождение. Первая часть названия показывает количество граней из которых состоит фигура, а слово эдр
произошло от древнегреческого слова «эдра» — грань.
Еще одной известной школой, которая занималась вопросами геометрии, является Александрийская философская школа. Выходцем этой школы был знаменитый ученый Евклид, который жил около трехсотого года до нашей эры.
Эвклид
ок. 325 — 265 гг. до н. э.
Евклид является автором «Начала», работы, которая состоит из тринадцати книг и содержит изложение планиметрии, стереометрии, ряда вопросов теории чисел. Этой работой Евклид создал фундамент дальнейшего развития математики. До сих пор этот труд считается основой изучения курса геометрии.
Он сформулировал 5 постулатов:
1. Через две точки можно провести прямую.
2. Отрезок прямой можно продолжить неограниченно.
3. Из всякого центра любым расстоянием можно описать окружность.
4. Все прямые углы равны между собой.
5. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше 2-х прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше 2-х прямых.
Широко известен факт о том, что царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его «Начала». На что Евклид ответил: «В геометрии нет царского пути».
В 19 веке в геометрии появились новые методы, которые позволили переводить геометрические задачи на язык алгебры и наоборот. Возникли и развиваются новые направления геометрических исследований: геометрия Лобачевского, проективная геометрия, топология, компьютерная геометрия и так далее.
В 1829 году русский математик Николай Лобачевский написал работу «О началах геометрии», в которой заявил, что можно построить геометрию такую же содержательную и свободную от противоречий, как и евклидова. Если геометрию Евклида можно назвать геометрией земных пространств и расстояний, то геометрия Лобачевского – геометрия гигантских межпланетных и исчезающих малых атомных пространств, она включает геометрию Евклида как составную часть, как частный случай.
Николай Иванович Лобачевский
1792 – 1856 гг
Основное отличие геометрии Лобачевского от геометрии Евклида заключается в так называемом «пятом постулате». Евклид утверждал, что «Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её»
. В геометрии Лобачевского вместо этой аксиомы принимается другая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
В 1899 году немецкий математик Давид Гильберт написал труд «Основания геометрии». Эта работа стала образцом для дальнейших работ по аксиоматическому построению геометрии.
Давид Гильберт
1862 – 1943 гг
Геометрические тела как и все геометрические фигуры являются воображаемыми объектами. Геометрическое тело – часть пространства, отделенное от остальной части пространства границей этого тела. Другими словами, мы представляем геометрические тела «пустыми», то есть есть оболочка, а внутри находить пустое пространство. Например, границей шара является сфера. По аналогии с планиметрией, когда окружность – являлась границей круга. Для каждого тела можно провести плоскость, по обе стороны которой будут находится точки этого тела. Такая плоскость является секущей.
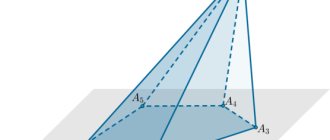
При изучении пространственных фигур пользуются изображением этих фигур на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одну и ту же фигуру можно изобразить по разному. Например, пирамиду можно изобразить так:
Штриховыми линиями изображаются невидимые части фигуры.
Обычно выбирают то изображение, которое создает правильное представление о форме фигуры и наиболее удобно для исследования ее свойств. Очевидно, что для изображения пирамиды мы выберем вот этот чертеж.
В 9 классе мы рассмотрим только несколько геометрических тел. Такие как призма, пирамида, цилиндр, конус, шар. При этом мы будем в основном опираться на наглядные представления. Более подробно эти тела мы будем изучать в курсах геометрии 10 и 11 классов.
Конспект урока геометрии в 9 классе на тему: Предмет стереометрии. Многогранник
Конспект урока геометрии для 9 класса
Предмет стереометрии. Многогранник.
Автор:
Плетнёв Александр Андреевич.
Место работы:
МБОУ Комсомольская СОШ п. Тюльпаны Заветинского района Ростовской области
Педагогический стаж:
3 года
Цели: познакомить учащихся с новым разделом геометрии — стереометрией, с геометрическими телами и их поверхностями; рассмотреть различные многогранники и научить учащихся изображать их. Ход урока
I Изучение нового материала
Учитель: Здравствуйте, дети! Сегодняшний урок мы проведем с Вами в форме лекции, однако в некоторых моментах вы будете помогать мне. До сих пор мы с Вами занимались изучением какого раздела геометрии? Дети: Планиметрии Учитель: Правильно, мы изучали планиметрию. А кто может дать определение планиметрии? Дети: Планиметрия – раздел геометрии, который изучает свойства плоских геометрических фигур, т.е. фигур, которые целиком расположены в некоторой плоскости. Учитель: Все верно, но если мы посмотрим на окружающие нас предметы, они являются плоскими? Дети: Нет. Учитель: Правильно, они не плоские, любой предмет который нас окружает занимают какую-то часть пространства. Вот как раз на сегодняшнем уроке, мы с Вами познакомимся с новым для Вас разделом геометрии, который называется стереометрией. Как и практически все новые понятия в математике, это слово также имеет греческое происхождение, «стереометрия» происходит от двух греческих слов: «стерео» — объемный, пространственный и «метрео» — измерять. В стереометрии также рассматриваются простейшие фигуры, что и в планиметрии. Кто может напомнить простейшие фигуры планиметрии? Дети: точка, прямая, плоскость. Учитель: Молодцы. Помимо простейших фигур, которые вы перечислили, в стереометрии рассматриваются геометрические тела и их поверхности. Представления о геометрических телах дают нам окружающие нас предметы. Если мы рассмотрим поверхность кристалла, то можем заметить, что он состоит из некоторого количества многоугольников. Такие поверхности в стереометрии называются многогранниками. Самым простейшим многогранником является куб.
Учитель: Существует несколько важных понятий, присущих многогранникам: • Вершина • Ребро • Грань • Диагональ Посмотрите на рисунок и попробуйте сформулировать определение грани, ребра и вершины. Дети: Грани – это многоугольники, из которых составлен многогранник. Ребра – стороны граней. Вершины – концы рёбер. Учитель: Верно, ребята! Однако ваше определение грани следует дополнить, «грани- это многоугольники, из которых составлен многогранник, причем никакие две соседние грани не лежат в одной плоскости». Осталось нам ввести понятие диагонали. Диагональ – отрезок, соединяющий две вершины, не принадлежащие одной грани. А теперь посмотрите внимательно на рисунок, и скажите сколько граней, ребер и вершин имеет куб? Дети: 6 граней, 12 ребер, 8 вершин Учитель: Правильно. Куб – это не единственно геометрическое тело, помимо него есть еще множество тел: шар, цилиндр, параллелепипед, пирамида, конус. конус параллелепипед пирамида цилиндр шар (сфера) тетраэдр
II. Закрепление изученного материала
Учитель: Ребята, давайте попробуем с помощью полученных сегодня знаний решим кроссворд. Разгадайте кроссворд в картинках, в качестве слов используя наиболее близкие геометрические тела, схожие с домом. — 1
— 2 — 3 — 4 — 5 — 6
ответы:
III Итоги урока.
Учитель: Ребята, объясните, что такое многогранник; что такое грани, ребра, вершины и диагонали многогранника. Приведите примеры многогранников.
IV Задание на дом.
Учитель: домашнее задание: изучить пункты 118 и 119 учебника; решить задание № 1184.
Рекомендуем посмотреть:
Урок математики по теме Диаграммы в 6 классе Игра «Поле чудес» по математике для учащихся 5-6 классов коррекционных школ VIII вида Внеклассное мероприятие по математике для учащихся коррекционных школ VIII вида Конспект урока математики в 5 классе «Путешествие в страну Математики»
Похожие статьи:
Игра как средство интерактивного обучения по предмету Математика
Конспект урока математики в 6 классе по теме: Умножение и деление обыкновенных дробей
Внеклассное мероприятие по математике для учащихся 7-8 класса. Игра «Слабое звено»
Конспект урока математики 9 класс по теме: Арифметическая и геометрическая прогрессии
Конспект урока математики в 5 классе по теме: Умножение и деление десятичных дробей на натуральные числа