Словарь терминов по математике от А до Я
Аксиома — утверждение, принимаемое 6ез доказательств.
Алгебраическое выражение — некоторое количество чисел, обозначенных буквами или цифрами и соединенных при помощи действий сложения, вычитания, умножения, деления, возведения в степень и извлечения корня.
Абцисса (французское слово). Одна из точек декартовых координат. Является первой. Обозначается, обычно, символом «X». Впервые употреблено Г. Лейбницем в 1675 году (немецкий ученый).
Аддитивность. Некоторое свойство величин. Говорит о следующем: значение определенной величины соответствующее полноценному объекту, равно сумме значений такой величины, которые соответствуют его частям в любом разбиении полноценного объекта на части.
Адъюнкта. Полностью соответствует алгебраическому дополнению.
Аксонометрия. Один из способов изображения на плоскости пространственных фигур.
Алгебра. Часть математики, которая изучает задачи и решения алгебраических уравнений. Термин впервые возможно было увидеть в 11-м веке. Применил Мухам меда бен-Муса ал-Хорезми (математик и астроном).
Аргумент (функции). Переменная величина (независимая), с помощью которой определяется значение функции.
Арифметика. Наука, которая изучает действия над числами. Возникла в Вавилоне, Индии, Китае, Египте.
Ассиметрия. Отсутствие или нарушение симметрии (обратное значение симметрии).
Бесконечно большая величина — больше любого наперед заданного числа.
Бесконечно малая величина — меньше любой конечной.
Биллион. Одна тысяча миллионов (единица с девятью нулями).
Биссектриса. Луч, имеющий начало в вершине угла (делит угол на две части).
Вектор. Направленный отрезок прямой. Один конец — начало вектора; другой — конец вектора. Впервые термин употребил У. Гамильтон (ирландский ученый).
Вертикальные углы. Пара углов, которая имеет общую вершину (образуется за счет пересечения двух прямых таким образом, что стороно одного угла — это прямое продолжение второго).
Вектор — величина, характеризующаяся не только своим числовым значением, но и направлением.
График — чертеж, наглядно изображающий зависимость одной величины oт другой, линия, дающая наглядное представление о характере изменения функции.
Гексаэдр. Шестигранник. Термин впервые был употреблен Паппой Александийским (древнегреческий ученый).
Геометрия. Часть математики, которая изучает пространственные формы и отношения. Термин впервые употребили в Вавилоне/Египте (5 ве до н. э.).
Гипербола. Незамкнутая кривая (состоит при помощи двух неограниченных ветвей). Термин появился благодаря Апполонию Пермскому (древнегреческий ученый).
Гипоциклоида. Это кривая, которую описывает точка окружности.
Гомотетия. Расположение между собой фигур (подобных), при которых прямые, соединяющие точки этих фигур, пересекаются в одной и той же точке (это называется центр гомотетии).
Градус. Единица измерения для плоского угла. Равна 1/90 части прямого угла. Измерять углы в градусах начала больше 3 веков назад. Впервые такие измерения применили в Вавилоне.
Дедукция. Форма мышления. С ее помощью какое-либо утверждение выводят логически (исходя из правил современной науки «логики»).
Диагональ. Отрезок прямой, который между собой соединяет вершины треугольника (они не лежат на одной стороне). Впервые употребил термин Евклид (3 век до нашей эры).
Дискриминант. Выражение, составленное из величин, определяющих функцию.
Дробь — число, составленное из целого числа долей единицы. Выражается отношением двух целых чисел m/n, где m — числитель, показывающий, сколько долей единицы содержится в дроби, а n знаменатель, показывающий, на сколько долей разделена единица.
Знаменатель. Числа, из которых составляют дробь.
Золотое сечение — деление отрезка на две части так, что большая часть, относится к меньшей так, как весь отрезок — к большей части. Приблизительно равно 1,618. Критерий красоты, используется в архитектуре и др. Термин ввел Леонардо да Винчи.
Индекс. Буквенный либо числовой указатель. С его помощью снабжается математические выражения (делается это для того, чтобы отличать друг от друга).
Индукция. Метод доказательства математического уравнения.
Интеграл. Основное понятие математического анализа. Возникло из-за того, что понадобилось измерять объемы и площади.
Иррациональное число. Число, которое не является рациональным.
Катет. Одна из сторон прямоугольного треугольника, которая прилежит к прямому углу.
Квадрат. Правильный четырехугольник (либо ромб). Каждый угол квадрата прямой. Все углы в квадрате равны (по 90 градусов).
Математическая константа. Величина, которая никогда не изменяется в своем значении. Константа — противоположное число для переменной.
Конус. Тело, которое ограничено одной полостью при помощи конической поверхности. Оно пересекает плоскость (плоскость перпендикулярна ее оси).
Косинус. Является одной из тригонометрических функций. Обозначение в математике/высшей математике — cos.
Корень уравнения — решение, значение неизвестного, найденное через известные коэффициенты.
Константа — постоянная величина.
Координаты — числа, определяющие положение точки на плоскости, поверхности или в пространстве.
Логарифм. Показатель степени «m». Его следует возвести в степень «а» для того, чтобы получить некоторое число NT. Впервые логарифм предложил Дж. Непер.
Линия — общая часть двух смежных областей поверхности.
Максимум. Наибольшее значение функции.
Масштаб. Отношение двух линейных размеров по отношению друг к другу. Используется во многих современных отраслях. Основная — картография, геодезия.
Матрица. Прямоугольная таблица. Образуется при помощи множества числа (определенного). Включает в себя столбцы и строки (структура матрицы). Впервые термин «матрица» появилась у ученого Дж. Сильвестра.
Медиана. Отрезок, который соединяет вершину треугольника и его середину противоположной стороны.
Минимум. Наименьшее значение функции.
Многоугольник. Геометрическая фигура. Определение — замкнутая ломаная.
Модуль. Абсолютная величина (действительного числа).
Множество — совокупность элементов, объединенных по какому-нибудь признаку.
Норма. Абсолютная величина числа.
Неравенство — два числа или выражения, соединенных знаками (больше) или (меньше).
Овал. Выпуклая, замкнутая фигура (плоская).
Окружность. Многочисленные точки, расположенные на плоскости.
Ордината. Одна из декартовых координат. Обозначается, обычно, второй.
Октаэдр. Геометрическая фигура. Один из пяти многогранников (правильных). Октаэдр включает в себя 8 граней (правильных), 6 вершин и 12 ребер.
Параллелепипед. Призма. Основание — параллелограмм или многогранник (равносильные понятия). Имеет 6 граней. Каждая грань — параллелограмм.
Параллелограмм. Четырехугольник. Противолежащие стороны у него параллельны (попарно). На данный момент присутствует 2 частных случая параллелограмма: ромб и квадрат. Главное свойство данной геометрической фигуры: • Противоположные стороны равны; • Противоположные углы равны.
Периметр. Сумма всех сторон геометрической фигуры. Впервые удалось встретить у Архимеда и Герона (древнегреческие ученые).
Перпендикуляр. Прямая, которая пересекает плоскость (любую), находящуюся под прямым углом.
Пирамида. Многогранник. Его основание — это многоугольник. Любая другая грань — треугольник (эти грани имеют общую вершину). На данный момент пирамиды могут быть различных типов: треугольные, четырехугольные и так далее (различают таковые при помощи определения числа углов).
Планиметрия. Одна из наиболее важных частей элементарной (простой) геометрии. Планиметрия изучает свойства фигур, которые находятся на плоскости. Впервые термин был обозначен Еквлидом (древнегреческий ученый).
Плюс. Знак, который обозначает математическое действие — сложение. Кроме того, при помощи плюса обозначаются положительные числа. Впервые знак ввел Я. Видман (знаменитый чешский ученый).
Предел. Основное понятие математики. Обозначает: переменная величина неограниченно приближается к постоянному значению (определенному). Впервые термин использовал известный ученый Ньютон.
Призма. Многогранник. Первые 2 грани — равные угольники (это есть основания призмы). Остальное — боковые грани.
Проекция. Один из способов изображения пространственных и плоских фигур.
Переменная — величина, числовое значение которой изменяется по определенному, известному или неизвестному закону.
Плоскость — простейшая поверхность. Любая прямая, соединяющая две ее точки, целиком принадлежит ей.
Прямая — совокупность точек, общих для двух пересекающихся плоскостей.
Процент — сотая часть числа.
Радиан. Единица для измерения углов.
Ромб. Параллелограмм. Все стороны у данной фигуры равны. Ромб, имеющие прмые углы, имеет термин «квадрат».
Сегмент. Часть круга (таковую ограничивают при помощи хорды, которая соединяет концы дуги).
Секанс. Тригонометрическая функция. Обозначение в математике/высшей математике — sec.
Сектор. Часть круга. Ограничивается при помощи окружности + двух радиусов (соединяет концы одной дуги с центром круга).
Симметрия — соответствие.
Синус. Тригонометрическая функция. Обозначение в математике/высшей математике — sin.
Стереометрия. Часть элементарной геометрии. Занимается изучением полноценных пространственных фигур.
Тангенс. Тригонометрическая функция. Обозначение в математике/высшей математике — tg.
Тетраэдр. Многогранник, включает в себя 4 треугольные грани. В каждой вершине по 3 грани (сходятся в вершинах). Тетраэдр имеет 4 грани + 6 ребер + 4 вершины.
Точка. Не имеет определенного и окончательного понятия. Любая точка обозначается при помощи букв A, B, C.
Треугольник. Многоугольник (простой). Включает в себя 3 вершины + 3 стороны;
Теорема — утверждение, которое нужно доказать исходя из аксиом и ранее доказанных теорем.
Тождество — равенство, справедливое при всех значениях входящих в него коэффициентов.
Топология — раздел математики, изучающий свойства фигур, не изменяющиеся при любых деформациях, проводимых 6ез разрывов и склеиваний.
Уравнение — математическая запись задачи о разыскании значений неизвестных, при которых значения двух данных функций равны.
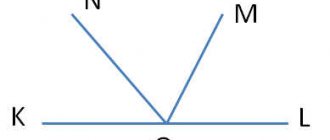
Угол. Геометрическая фигура (плоская). Образуется двумя лучами, которые выходят из одной точки (точки — вершины угла).
Факториал — произведение натуральных чисел от 1 до какого-либо данного натурального числа n. Обозначается n!. Факториал нуля о! = 1.
Формула — комбинация математических знаков, выражающая какое-нибудь предложение.
Функция — числовая зависимость между элементами двух множеств, при котором одному элементу одного множества соответствует определенный элемент другого множества. Может быть задана формулой или графиком.
Хорда. Отрезок, который соединяет между собой 2 точки, находящиеся на окружности.
Цифры — знаки для обозначения чисел.
Центр. Середина чего-либо (например: круга).
Цилиндр. Тело, которое ограничено цилиндрической поверхностью + параллельными плоскостями (двумя). Впервые понятие «цилиндр» возможно было встретить у Евклида и Аристарха.
Циркуль. Специальный прибор, разработанный для того, чтобы чертить дуги, линейные измерения и окружности.
Числитель. Определенное число, при помощи которого составлена дробь. Впервые термин применил Максим Плануда (византийский ученый).
Число — одно из основных понятий математики, возникшее в связи со счетом отдельных предметов.
Шар. Геометрическое тело. Представляет из себя общую совокупность всех точек определенного пространства.
Экспонента. Является одним и тем же, что и экспоненциальная функция. Впервые термин ввел Г. Лейбниц (немецкий ученый).
Эллипс. Овальная кривая. Впервые данный термин ввел Апполоний Пергский (древнегреческий ученый).
Словарь геометрических понятий 7-8 класс
Геометрия,7-9 Основные определения, теоремы, формулы
7 класс Глава I Начальные геометрические сведения
Первичные понятия: точка, прямая, плоскость, пространство
, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов
Отрезок
-часть прямой, ограниченная двумя точками.
Луч
-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны.
Угол
-часть плоскости, ограниченная двумя лучами, выходящими из одной точки.
Равные фигуры
-фигуры, которые совпадают при наложении друг на друга.
Середина отрезка
-точка на отрезке, делящая его пополам.
Биссектриса угла
-луч, выходящий из вершины угла и делящий его пополам.
Единицы измерения длины
отрезка: миллиметры, сантиметры, дециметры, метры, километры.
Единицы измерения углов
: градус, минуты, секунды.
Длина отрезка
-количество единиц измерения длины, вмещающихся между двумя концами отрезка.
Градусная мера угла
-количество единиц измерения углов, вмещающихся между сторонами угла.
Прямой угол
-угол,градусная мера которого равна 900.
Острый угол
-угол,градусная мера которого меньше 900.
Тупой угол
-угол,градусная мера которого больше 900,но меньше 1800.
Развёрнутый угол
-угол,градусная мера которого равна 1800.
Смежные углы
– это два угла, у которых одна сторона общая,а две других образуют прямую линию.
Свойство
: сумма смежных углов равна 1800.
Вертикальные углы
-два угла, у которых стороны одного угла являются продолжением сторон другого.
Свойство
: вертикальные углы равны.
Перпендикулярные прямые
-прямые, которые при пересечении образуют прямой угол.
Параллельные прямые
-прямые, лежащие в одной плоскости и не имеющие общих точек.
Глава II Треугольники
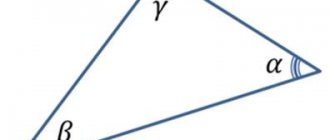
Треугольник
-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника.
Периметр
– сумма длин всех сторон.
Теорема(первый признак равенства треугольников
): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема
: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Медиана треугольника
— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника
— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника
— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник
-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.
Равносторонний треугольник
— треугольник, у которого все стороны равны.
Свойство
:в равнобедренном треугольнике углы при основании равны.
Свойство
:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Теорема(второй признак равенства треугольников)
: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема(третий признак равенства треугольников)
: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Окружность
-геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки-центра.
Радиус окружности
-отрезок,соединяющий любую точку окружности с её центром.
Хорда
-отрезок, соединяющий две любые точки окружности.
Диаметр
-хорда, проходящая через центр.
Дуга
– часть окружности, ограниченная двумя точками.
Основные задачи на построение циркулем и линейкой:
- построение отрезка, равного данному
- построение угла, равного данному
- построение биссектрисы угла
- построение середины отрезка
- построение перпендикулярных прямых
Глава III Параллельные прямые
При пересечении двух прямых третьей прямо-секущей образуются следующие виды углов:
- накрест лежащие углы
- односторонние углы
- соответственные углы
Теорема(первый признак параллельности прямых)
:если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема(второй признак параллельности прямых):
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема(третий признак параллельности прямых)
:если при пересечении двух прямых секущей сумма внутренних односторонних углов равна углы равна 1800, то прямые параллельны.
Аксиома
: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Теорема
:если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Теорема
:если две прямые параллельны третьей прямой, то они параллельны.
Теорема
:если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Теорема
:если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема
:если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 1800.
Глава IV Соотношения между сторонами и углами треугольника
Теорема
: сумма внутренних углов треугольника равна 1800.
Внешний угол треугольника
-угол, смежный с каким-либо внутренним углом треугольника.
Остроугольный треугольник
-это треугольник, все внутренние углы которого острые.
Тупоугольный треугольник
-это треугольник, у которого один из углов тупой.
Прямоугольный треугольник
-это треугольник, у которого один из углов прямой.
Гипотенуза
-это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Катеты
-это стороны прямоугольного треугольника, образующие прямой угол.
Теорема
:в треугольнике против большей стороны лежит больший угол.
Теорема
:в треугольнике против большего угла лежит большая сторона.
Следствие
:в прямоугольном треугольнике гипотенуза всегда больше катета.
Теорема(признак равнобедренного треугольника)
:если в треугольнике два угла равны, то он равнобедренный.
Теорема(неравенство треугольника)
:каждая сторона треугольника меньше суммы двух других сторон.
Свойство
:сумма двух острых углов треугольника равна 900.
Свойство
:катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Свойство
:если катет прямоугольного треугольника равен половине гипотенузы, то он лежит напротив угла в 300.
Теорема(признак равенства прямоугольных треугольников)
:если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):
если катет и прилежащий к нему острый угол одного прямоугольного треугольника равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников)
:если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников)
:если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой
– это длина перпендикуляра, опущенного из этой точки на прямую.
Теорема
:все точки каждой из двух параллельных прямых равноудалены от другой прямой.
8 класс. Глава V Четырёхугольники
Многоугольник
-фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Диагональ
-это отрезок, соединяющий две несоседних вершины многоугольника.
Выпуклый многоугольник
— это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема
:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм
— это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство
:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство
:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признак параллелограмма)
:Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма)
:Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма)
:Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция
-это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция
-это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция
-это трапеция, у которой один из углов прямой.
Теорема Фалеса
: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник
-это параллелограмм, у которого все углы прямые.
Свойство
: диагонали прямоугольника равны.
Теорема(признак прямоугольника):
если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб
-это параллелограмм, у которого все стороны равны.
Свойство
: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат
-это прямоугольник, у которого все стороны равны.
Глава VI Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Единицы измерения площади: мм2,см2, дм2, м2, ар=100м2, км2 , га=100км2.
Площадь квадрата
равна квадрату его стороны.
Площадь прямоугольника
равна произведению его смежных сторон.
Площадь параллелограмма
равна произведению его основания на высоту.
Площадь треугольника
равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника
равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции
равна полусумме её оснований на высоту.
Теорема Пифагора
:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.)
:если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Глава VII Подобные треугольники
Отрезки
mиnпропорциональны
отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники
— это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия-
это число, равное отношению сходственных сторон подобных треугольников.
Теорема
: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка:
биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников)
:если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников
):если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников)
:если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника
– это отрезок, соединяющий середины двух его сторон.
Теорема
:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус
острого угла прямоугольного треугольника- это отношение противолежащего катета к гипотенузе.
Косинус
острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.
Тангенс
острого угла прямоугольного треугольника- это отношение противолежащего катета к прилежащему .
Котангенс
острого угла прямоугольного треугольника- это отношение прилежащего катета к противолежащему .
Глава VIII Окружность
Касательная к окружности
– это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол
– это угол с вершиной в центре окружности.
Дуга окружности
измеряется центральным углом, который на неё опирается.
Вписанный угол
– это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
9 класс
Средняя линия трапеции
— это отрезок, соединяющий середины её боковых сторон.
Теорема
:средняя линия трапеции равна полусумме её оснований и параллельна им.
СОШИ «Умид»
Матема́тика (др.-греч. μᾰθημᾰτικά < др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке.
Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Представляем вашему вниманию словарь математических терминов.
Абсцисса — (лат. слово abscissa — «отрезанная»). Заимств. из франц. яз. в начале 19 в. Франц. abscisse – из лат. Это одна из декартовых координат точки, обычно первая, обозначаемая буквой x. В современном смысле Т. употреблен впервые немецким ученым Г. Лейбницем (1675).
Аддитивность — (лат. слово additivus – «прибавляемый»). Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части.
Адъюнкта — (лат. слово adjunctus – «присоединенный»). Это то же, что и алгебраическое дополнение.
Аксиома — (греч. слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В рус.яз. – с Петровских времен. Это основное положение, самоочевидный принцип. Впервые Т. встречается у Аристотеля. Использовался в книгах Евклида «Начала». Большую роль сыграли работы древнегреческого ученого Архимеда, который сформулировал аксиомы, относящиеся к измерению величин. Вклад в аксиоматику внесли Лобачевский, Паш, Пеано. Логически безупречный список аксиом геометрии был указан немецким математиком Гильбертом на рубеже 19 и 20 вв.
Аксонометрия — (от греч. слова akon – «ось» и metrio – «измеряю»). Это один из способов изображения пространственных фигур на плоскости.
Алгебра — (араб. слово «ал-джебр»). Это часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Т. впервые появляется у выдающегося математика и астронома 11 века Мухаммеда бен-Мусы ал-Хорезми.
Анализ — (греч. слово analozis – «решение», «разрешение»). Т. «аналитическая» восходит к Виету, который отвергал слово «алгебра» как варварское, заменяя его словом «анализ».
Аналогия — (греч. слово analogia – «соответствие», «сходство»). Это умозаключение по сходству частных свойств, имеющихся у двух математических понятий.
Антилогарифм — (лат. слово nummerus – «число»). Это число, которое имеет данное табличное значение логарифма, обозначается буквой N.
Антье — (франц. слово entiere – «целый»). Это то же, что целая часть действительного числа.
Апофема — (греч. слово apothema,apo – «от», «из»; thema – «приложенное», «поставленное»). 1.В правильном многоугольнике апофема – отрезок перпендикуляра, опущенного из его центра на любую из его сторон, а также его длина. 2.В правильной пирамиде апофема – высота любой его боковой грани. 3.В правильной усеченной пирамиде апофема – высота любой ее боковой грани.
Аппликата — (лат. слово applicata – «приложенная»). Это одна из декартовых координат точки в пространстве, обычно третья, обозначаемая буквой Z.
Аппроксимация — (лат.слово approximo – «приближаюсь»). Замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аргумент функции (лат. слово argumentum – «предмет», «знак»). Это независимая переменная величина, по значениям которой определяют значения функции.
Арифметика (греч. слово arithmos – «число»). Это наука, изучающая действия над числами. Арифметика возникла в странах Др. Востока, Вавилона, Китае, Индии, Египте. Особый вклад внесли: Анаксагор и Зенон, Евклид, Эратосфен, Диофант, Пифагор, Л. Пизанский и др.
Арктангенс, Арксинус (приставка «арк»- лат. слово arcus – «лук», «дуга»). Arcsin и arctg появляются в 1772 году в работах венского математика Шеффера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернулли, но который употреблял другую символику.
Асимметрия (греч. слово asymmetria – «несоразмерность»). Это отсутствие или нарушение симметрии.
Асимптота (греч. слово asymptotes – «несовпадающий»). Это прямая, к которой неограниченно приближаются точки некоторой кривой по мере того, как эти точки удаляются в бесконечность.
Астроида (греч. слово astron – «звезда»). Алгебраическая кривая.
Ассоциативность (лат. слово associatio – «соединение»). Сочетательный закон чисел. Т. введен У.Гамильтоном (1843).
Биллион (франц. слово billion, или миллиард – milliard). Это тысяча миллионов, число изображаемое единицей с 9 нулями, т.е. число 10 9 . В некоторых странах биллионом называют число, равное 10 12.
Бином (лат. слова bi – «двойной», nomen – «имя) сумма или разность двух чисел или алгебраических выражений, называемых членами бинома.
Биссектриса (лат. слова bis – «дважды» и sectrix –«секущая»). Заимств. В 19 в. из франц. яз. где bissectrice – восходит к лат. словосочетанию. Это прямая, проходящая через вершину угла и делящая его пополам.
Вектор (лат. слово vector – «несущий», «носитель»). Это направленный отрезок прямой, у которой один конец называют началом вектора, другой конец – концом вектора. Этот термин ввел ирландский ученый У. Гамильтон (1845).
Вертикальные углы (лат. слова verticalis – «вершинный»). Это пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Гексаэдр (греч. слова geks – «шесть» и edra – «грань»). Это шестигранник. Этот Т. приписывают древнегреческому ученому Паппу Александрийскому (3 век).
Геометрия (греч. слова geо – «Земля» и metreo – «измеряю»). Др.-рус. заимств. из греч.яз. Часть математики, изучающая пространственные отношения и формы. Т. появился в 5 веке до н.э. в Египте, Вавилоне.
Гипербола (греч. слово hyperballo – «прохожу через что-либо»). Заимств. в 18 в. из лат. яз. Это незамкнутая кривая из двух неограниченно простирающихся ветвей. Т.ввел древнегреческий ученый Апполоний Пермский.
Гипотенуза (греч.слово gyipotenusa – «стягивающая»). Замств. из лат. яз. в 18 в., в котором hypotenusa – от греч. сторона прямоугольного треугольника, лежащая против прямого угла. Древнегреческий ученый Евклид (3 век до н.э.) вместо этого термина писал, «сторона, которая стягивает прямой угол».
Гипоциклоида (греч. слово gipo – «под», «внизу»). Кривая, которую при этом описывает точка окружности.
Гониометрия (лат. слово gonio – «угол»). Это учение о «тригонометрических» функциях. Однако это название не привилось.
Гомотетия (греч. слово homos- «равный», «одинаковый», thetos — «расположенный»). Это расположение подобных между собой фигур, при котором прямые, соединяющие соответствующие друг другу точки фигур, пересекаются в одной и той же точке, называемой центром гомотетии.
Градус (лат. слово gradus – «шаг», «ступень»). Единица измерения плоского угла, равная 1/90 части прямого угла. Измерение углов в градусах появилось более 3 лет назад в Вавилоне. Обозначения, напоминающие современные, использовались древнегреческими ученым Птолемеем.
График (греч. слово graphikos- «начертанный»). Это график функции – кривая на плоскости, изображаемая зависимость функции от аргумента.
Дедукция (лат. слово deductio-«выведение»). Это форма мышления, посредством которой утверждение выводится чисто логически (по правилам логики) из некоторых данных утверждений – посылок.
Деференты (лат. слово defero-«несу», «перемещаю»). Это окружность, по которой вращаются эпициклоиды каждой планеты. У Птолемея планеты вращаются по окружностям – эпициклам, а центры эпициклов каждой планеты вращаются вокруг Земли по большим окружностям – деферентам.
Диагональ (греч. слово dia – «через» и gonium – «угол»). Это отрезок прямой, соединяющий две вершины многоугольника, не лежащие на одной стороне. Т. встречается у древнегреческого ученого Евклида (3 век до н.э.).
Диаметр (греч. слово diametros – «поперечник», «насквозь», «измеряющий» и слово dia – «между», «сквозь»). Т. «деление» в русском языке впервые встречаются у Л.Ф.Магницкий.
Директриса (лат. слово directrix – «направляющий»).
Дискретность (лат. слово discretus – «разделенный», «прерывистый»). Это прерывность; противопоставляется непрерывности.
Дискриминант (лат. слово discriminans- «различающий», «разделяющий»). Это составленное из величин, определенных заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы.
Дистрибутивность (лат. слово distributivus – «распределительный»). Распределительный закон, связывающий сложение и умножение чисел. Т. ввел франц. ученый Ф. Сервуа (1815 г.).
Дифференциал (лат. слово differento- «разность»). Это одно из основных понятий математического анализа. Этот Т. встречается у немецкого ученого Г. Лейбница в 1675 г. (опубликовано в 1684г.).
Дихотомия (греч.слово dichotomia – «разделение надвое»). Способ классификации.
Додекаэдр (греч. слова dodeka – «двенадцать» и edra – «основание»). Это один из пяти правильных многогранников. Т. впервые встречается у древнегреческого ученого Теэтет (4 век до н.э.).
источник