Задачи по геометрии на повторение 7 класс
Задачи по теме « Равнобедренный треугольник»
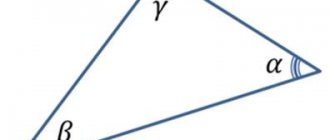
1. В треугольнике АВС углы ВАС и ВСА равны, их биссектрисы АА1 и СС1 пересекаются в точке О. Докажите, что треугольник АОС равнобедренный.
2. Найдите периметр треугольника АВС если два его угла равны, а две стороны имеют длины 40 см и 20см.
3. В треугольнике АВС угол В=1200 , а угол А= 300 . Точка D принадлежит стороне АС, причем угол ВDС тупой. Докажите, что АВ ВD.
4.Разность длин двух сторон равнобедренного тупоугольного треугольника равна 4 см, а его периметр равен 19 см.Найдите длины сторон треугольника.
5. В равнобедренном треугольнике АВС угол В — тупой. Высота ВD равна 4 см. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 12 см.
6.В треугольнике АВС внешние углы при вершинах А и С равны. Найдите длину биссектрисы ВD , если периметр треугольника АВС равен 72 см, а периметр треугольника АВD равен 48 см.
Задачи по теме « Признаки равенства треугольников»
1. На высоте АН равнобедренного треугольника с углом А=900 взята точка О. Докажите, что треугольники ВОН и НОС равны.
2. В треугольнике КМР КМ=МР. Точки А и В середины сторон KM и MP соответственно. АС и ВD перпендикулярны прямой КР. Докажите, что треугольники КАС и DВР равны.
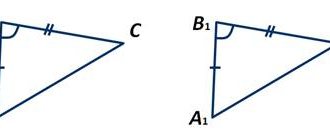
3. Даны равносторонние треугольники АВС и А1В1С1 точки О и О1 – точки пересечения высот этих треугольников, причем ОА= О1А1 . Докажите, что треугольники АВС и А1В1С1 равны.
4. Треугольник АВС равносторонний. AC – основание. Точки К , L , М- середины сторон АВ , ВС и АС соответственно . Докажите, что треугольники АКМ и МLC равны.
5. Даны треугольники АВС , с высотой СН , и KMN с высотой NL . Причем , угол В=600, угол М=600, СН=LN и АВ=KM. Докажите , что треугольники АВС и KMN равны.
6. В равнобедренном треугольнике АВС ВК – медиана, проведенная к основанию. Точки М и N принадлежат боковым сторонам. Луч КВ – биссектриса угла МКN . Докажите, что АМ=NC.
Задачи по теме « Окружность»
1. В окружности с центром О проведены радиусы ОК , ОМ , ОN , таким образом ,что углы КОМ и МОN равны. Докажите , что треугольники КОМ и МОN равны.
2. В окружности с центром О диаметру АС перпендикулярен радиус ОВ. Докажите, что АВ=ВС.
3. В окружности с центром О проведены две непараллельные хорды КМ и РN , причем КМ= РN. Точка А – середина КМ, точка В – середина Р N . Докажите, что треугольник АОВ равнобедренный.
Задачи по теме «Смежные и вертикальные углы»
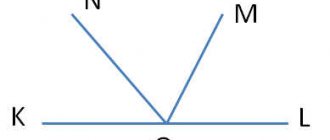
1. Один из углов, образовавшихся при пересечении двух прямых равен 480 .Найти остальные углы.
2. Дан треугольник АВС. На продолжении сторон АВ и ВС за вершину В отмечены точки К и М соответственно. Угол КВМ=300 Угол А в 3 раза больше угла С. Найти угол, смежный с углом С.
3. На окружности с центром О последовательно отмечены точки А, В, С, D, К так, что точки А и К являются концами диаметра, углы АОС и СОК равны. Угол АОВ= 300 , угол DОК=600 . Докажите, что ВD=АС.
Задачи по теме «Параллельные прямые»
1. Отрезки KM и PL –диаметры некоторой окружности. Докажите, что прямые KP и ML параллельны.
2. Точки А и С лежат по разные стороны от прямой BD . Известно, что АВ параллельна DC и AD параллельна ВС. Докажите, что угол BAD равен углу DCB, АВ=DC и AD= BC.
3. На биссектрисе CD равнобедренного треугольника АВС взята точка М. Через эту точку проведены прямые, параллельные сторонам АС и ВС и пересекающие основание АВ в точках Н и К. Докажите, что АН=КВ.
4. На сторонах MP и PN треугольника MPN взяты точки А и В соответственно. Угол PMN равен углу РАВ и равен 600, угол MNP равен 500. Найдите, чему равен угол АВN.
5. В треугольнике АВС угол А равен 300, угол С равен 1200. Докажите, что биссектриса внешнего угла при вершине С лежит на прямой, параллельной прямой АВ.
6. На одной стороне неразвернутого угла взяты точки E и F, на другой – G и H , так, чтобы EG параллельно FH , точка М принадлежит отрезку EG , угол MFE равен углу MFH, угол MHF равен MHG. Докажите, что EG= EF+GH.
Первые уроки геометрии в 7 классе
4. Различные прямые аи с
пересекаются в точке
А.
Прямая апроходит через точку
D.
Проходит ли через точку D
прямая
с
? Объясните ответ.
Решение. Прямая с
не проходит через точку
В,
так как две различные прямые могут пересекаться только в одной точке
(по основному свойству
I).
5. Одна из двух пересекающихся прямых проходит через точку А,
принадлежащую другой прямой. Различны ли точка
А
и точка пересечения данных прямых? Объясните ответ.
Решение. Эти точки совпадают, так как две прямые могут пересекаться только в одной точке(по основному свойству
I).
Диктант
Диктант планируется на 10 мин. Провести его рекомендуется наследующем уроке вместо проверки домашнего задания.
1°. Проведите прямую, обозначьте ее двумя способами.
2°. Проведите прямую а,
отметьте точку С, которая лежит на прямой
а,
точку
В,
котораяне лежит на прямой
а.
Проведите прямую с
,
проходящую через точку
В
и пересекающую прямую
а.
Обозначьте точку пересечения прямых буквой
Р.
3. Проведите прямую а,
отметьте две точки
А
и
В,
лежащие на прямой
а.
Можно ли через точки
А
и
В
провести прямую с
,
отличную от прямой а? Объясните ответ. (Дополнительная задача включается по усмотрению учителя.)
3,4,5. Отрезок.Измерение отрезков.
Полуплоскости (2 ч)
Начиная с пункта «Измерение отрезков», нужно постепенно проводить работу по обучению учащихся доказательным рассуждениям, акцентируя внимание на обосновании решения задач, требовать от них более точные геометрические формулировки.
2.Для закрепления терминологии, связанной сописанием взаимного расположения точек на прямой,можно предложить учащимся выполнить упражнение 5 из учебника, дополнив его вопросами:
1) отметьте точку В
так, чтобы точка
В разделяла (лежала между)
точки
А
и
В;
2) отметьте точку
Р
так, чтобы точка
Р лежала между (разделяла)
точками
А
и
В.
Выполнение этого упражнения сводится к изображению на доске и в тетрадях учащихся по заданному в упражнении описанию ситуации, а также к последующему устному описанию (проговариванию) ситуации по рисунку. При необходимости ответы учащихся уточняются и корректируются учителем. Записей условия задачи и ее заключения не делается.
3°. Формулируя основное свойство взаимногорасположения точек на прямой (основное свойствоII), следует обратить внимание на то, что вэтом свойстве содержатся два утверждения: существования точки («Из трех точек на прямой одналежит между двумя другими») и ее единственности («Из трех точек на прямой только одна лежит между двумя другими»).
4°. В формулировках ряда задач, относящихся в учебнике к измерению отрезков, говорится о трехточках, лежащих на одной прямой (рис. 4). Непосредственное применение основного свойства измерения отрезков (основное свойство III) при доказательных рассуждениях ведет к потере одногологического шага, а именно: если одна (точка А)
из трех точек
(А, В
и С) прямой лежит между двумя другими (рис. 8), то она принадлежит отрезку
ВС,
и, следовательно, по основному свойствуIII:
ВС = ВА + АС.
Открытый урок по геометрии 7 класс «признаки равенства треугольников»
Тема:
Повторение курса геометрии 7 класс. (признаки равенства треугольников)
Цели урока:
образовательные:
организовать деятельность учащихся по применению знаний при решении задач на применение элементов треугольника; признаков равенства треугольников.
развивающие:
— развитие ключевых компетенций;
— развитие навыков исследования через выполнение проектов по теме;
— формирование способности к оцениванию собственной деятельности.
воспитательные:
воспитание отношений взаимопомощи и сотрудничества между учащимися в процессе познавательной деятельности; развитие их самостоятельности и творчества.
Игра «Счастливый случай»
Ход урока
- I.
Организационный момент.
Класс делится на три команды, выбирается капитан каждой команды (всё это необходимо выполнить до начала урока). Каждая команда садится за свой «круглый стол». На каждом столе приготовлен лист учёта знаний, в котором капитаны напротив каждой фамилии ставят «+ «, если учащийся дал верный ответ. По итогам каждого гейма подсчитываются «+ «и ставятся в строке «всего».
- II.
Мотивация урока.
Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
Зовётся он треугольник,
И с ним хлопот не оберётся школьник!
Общий лист учёта (располагается на доске)
| Название гейма | I команда | II команда | III команда |
| Домашнее задание | |||
| I гейм “Разминка” | |||
| II гейм “Найди ошибку” | |||
| III гейм «Спешите видеть» | |||
| III гейм “Заморочки из бочки” | |||
| IV гейм «Ты мне я тебе» | |||
| Итого |
ХОД ИГРЫ
I гейм: «Разминка»
Каждой группе по очереди задаются вопросы, если какая-то группа не может дать ответ на поставленный вопрос, право ответить переходит к другой группе.
- Объясните, какая фигура называется треугольником.
- Что такое периметр треугольника?
- Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
- Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
- Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
- Какой треугольник называется равнобедренным?
- Какой треугольник называется равносторонним?
- Сформулируйте свойство углов при основании равнобедренного треугольника.
- Сформулируйте первый признак равенства треугольников.
- Сформулируйте второй признак равенства треугольников.
- Сформулируйте третий признак равенства треугольников.
- Какой треугольник называется прямоугольным?
- Как называется наибольшая сторона в прямоугольном треугольнике?
- Как называются стороны составляющие прямой угол?
- Чему равна сумма углов в треугольнике?
Пока команды отвечают на вопросы, капитаны команд в это время разгадывают кроссворд
| ||||||||
| 2 | ||||||||
| 5 | 1.Фигура , которая состоит из трех точек | |||||||
| 3 | не лежащих на одной прямой и трех отрезков | |||||||
| попарно соединяющих эти точки; | ||||||||
| 2. Если в треугольнике два угла равны, | ||||||||
| то этот треугольник … | ||||||||
| 1 | 3. Перпендикуляр , проведенный из данной | |||||||
| вершины треугольника к прямой, содержащей | ||||||||
| противолежащую сторону треугольника; | ||||||||
| 4 | 4. Отрезок, соединяющий данную вершину | |||||||
| с серединой противолежащей стороны | ||||||||
| треугольника; | ||||||||
| 5. Чем является медиана, проведенная | ||||||||
| к основанию равнобедренного треугольника. | ||||||||
II гейм “Найди ошибку”
Сейчас участники конкурса получат задание. Им нужно найти ошибки в высказываниях и записать правильные высказывания.
1 группа
- Два равнобедренных треугольника с одинаковыми основаниями равны.
- Если мы строим равнобедренный треугольник, то у него все углы равны.
2 группа
- Один раз поссорились стороны треугольника, одна сторона упала влево, другая вправо и треугольник распался на три прямых.
- “Смежные углы равны по 90 градусов”.
3 группа
- Два треугольника равны, если три угла одного треугольника соответственно равны трем углам другого треугольника.
- Высота любого треугольника проходит внутри треугольника.
III гейм «Спешите видеть»
1. Для каждой группы приготовлены чертежи на доске, по которым по очереди представители групп доказывают равенство треугольников.
Для 1 группы:
Для II группы:
Для III группы:
Физ.минутка бабочка (презентация)
IV гейм «Заморочки из бочки»
Каждая группа по очереди достаёт бочонок с номером. Под номером содержится задачу с готовым чертежом. В течение 2 — 3 минут вся группа обсуждает решение задачи, затем представители групп по очереди выходят к доске и показывают решение данной задачи.
Среди бочонков есть счастливый. Группа, вытянувшая такой бочонок получает призовые 2 очка.
Задачи по геометрии на повторение курса 7 класса
Задачи на повторение курса геометрии в 7 классе
1) Найдите величины смежных углов, если один из них в 5 раз больше другого. ( 30 и 50)
2) Отрезки MN
и
DK
пересекаются в их общей середине B. Докажите равенство треугольников
MDB
и
NKB
. (по 1 признаку)
3) Найдите периметр равнобедренного треугольника ADC
с основанием
AD
, если
AD
= 7 см,
DC
= 8 см.(23 )
4) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°(63 и 117)
5) Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR.(21 или 9)
6) Угол, противолежащий основанию равнобедренного треугольника, равен 50° . Найдите величину внешнего угла при основании.(115)
7) Найдите углы треугольника, на которые высота разбивает равносторонний треугольник.(30, 60 и 90)
 Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .(42 и 138)
Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° .(42 и 138)
9) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126° .(126 и 54)
10) Найдите смежные углы, если один из них на 55° больше другого.(62,5 и 117,5)
11) Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO.(1 признак)
12) Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что AC = 17 см, угол ABC равен 84°(42о и 8,5 см)
13) Отрезки AB
и
CM
пересекаются в точке O. Луч
OK
является биссектрисой угла
MOB
. Найдите угол
MOK,
если угол
AOM
равен 86° .(47)
14) В треугольнике MOK
O = 76°, а угол
M
в 3 раза меньше внешнего угла при вершине
K
. Найдите неизвестные углы треугольника.(38 и 114)
15) Найдите углы при основании MР
равнобедренного треугольника
МОР,
если
MK
– его биссектриса и
OKM =
96°.(64)
16) Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°.(42 и 138)
17) Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.(29 и 29)
18) В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.(8)
19) Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.(110)
20) Найти смежные углы, если один из них на 45 больше другого.(67,5 и 112,5)
21) Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.(8,8 и 17,6)
22) Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50 градусам. Найти эти углы.(115 и 65)
23) Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°.(63 и 117)
24) Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.(6 или 10)
25) В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС+АВ=18см. Найти AC и AB.(6 и 12)
26) Найдите все углы, образованные при пересечении двух параллельных прямых а
и
в
секущей
с
, если один из углов на 700 больше другого.(105 и 65)
Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе «Знакомьтесь. Геометрия».
Цели и задачи урока:
- Образовательные
: познакомить учащихся с историей возникновения
геометрии, с основоположниками геометрии, с основными геометрическими
понятиями – точкой и прямой, с их обозначениями, некоторыми
геометрическими фигурами на плоскости, повторить ранее
изученный геометрический материал.
- Воспитательные
: привитие интереса к предмету с помощью изучения
истории и развития науки, решения занимательных задач, формирование умения аккуратно и грамотно выполнять математические записи.
Оборудование:
компьютер, мультимедийный проектор, презентация
«Знакомьтесь. Геометрия», выполненная с помощью программы Microsoft Power Point 2003.
План урока.
- Вводное слово учителя (слайды № 1, 2).
- Рассказ учителя об истории возникновения и развитии геометрии
(слайд № 3), об основоположниках геометрии (слайд № 4, 5).
- Повторение известных геометрических фигур (слайд № 6).
- Введение основных геометрических фигур на плоскости и решение задач (слайды № 7,8).
- Рассказ о чертежных инструментах, необходимых на уроках геометрии (слайд № 9).
- Физкультминутка (слайд № 11).
- Рассмотрение геометрических иллюзий (слайды № 12, 13, 14).
- Решение занимательных задач (слайды № 15, 16).
Ход урока.
- Вводное слово.
Великий французский архитектор Ле Корбюзье в начале
XX века сказал: «Никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Действительно, мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира вам поможет новый предмет – геометрия.
А ученый Галилео Галилей сказал:
«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».
2. История возникновения геометрии.
Как возникла геометрия? Как сказал Эвдем Родосский: «Геометрия была открыта египтянами и возникла при измерении земли. Это измерение было им
необходимо вследствие разлития Нила, постоянно смывавшего границы. Нет ничего необычного в том, что эта наука, как и другие, возникла из потребностей человека». Значит, геометрия возникла из практической деятельности людей.
Нужно было сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры.
В переводе с греческого слово «геометрия» означает «землемерие»
(«гео» — земля, «метрио» — мерить). Удовлетворяя свои эстетические потребности, люди украшали орнаментами свое жилище, одежду. Овладевая окружающим миром, люди знакомились с геометрическими формами, они стали учиться измерять площади, длины, объемы.
Занятия людей в древности:
- Строительство храмов и домов;
- Украшение орнаментом посуды и жилищ;
- Разметка земли, измерение расстояний и площадей, объемов сосудов.
За несколько столетий до нашей эры в Вавилоне, Китае, Египте, Греции уже существовали начальные геометрические знания, которые добывались опытным путем, а затем систематизировались. Первым, кто начал получать новые геометрические факты при помощи рассуждений, был древнегреческий математик Фалес (6 век до нашей эры). Постепенно геометрия становится наукой. С V века до нашей эры начинается попытка греческих ученых привести геометрические факты в систему. Сочинение греческого ученого Евклида «Начала» почти 2000 лет было основной книгой, по которой изучали геометрию. Геометрия, изложенная в ней, стала называться евклидовой геометрией.
«В геометрии нет царских дорог»
Евклид – известный древнегреческий математик, родился в Афинах около 325 г. до н.э, был учеником Платона. В г.Александрия организовал математическую школу. Основная его работа «Начала», в которой он обработал все предыдущие достижения греческих математиков и создал фундамент для ее дальнейшего развития. Евклид сам сформулировал V постулат (аксиому) о параллельных прямых. Другие его работы:
- «Данные».
- «Явления».
- «Оптика».
- «Сечения канона».
Основоположники геометрии:
Платон основал школу, девиз которой «Не знающие геометрии не допускаются!»
(2400 лет назад).
Фалес Милетский (640-548 г.до н.э.).Евклид (III в. до н.э.).Пифагор (VI в до н.э.)
Рене Декарт (17 век).
- Повторить известные геометрические фигуры и сформулировать определение планиметрии.
- Введение основных фигур на плоскости.
Самое большое здание складывается из маленьких кирпичиков, так и сложные геометрические фигуры составляются из простейших фигур. Одна из них – точка
.
«Точка есть то, что не имеет частей» Евклид.
Точка – результат мгновенного касания, укол.
Точка обозначается: А, В, С… — большие буквы латинского алфавита
Прямая.
Она безгранична, на рисунке изображается только часть прямой.
Прямая МР или а – одна маленькая буква латинского алфавита или две большие.
Задания по готовому чертежу (слайд № 8):
- Назовите (двумя способами) прямые, изображенные на чертеже.
- Назовите точки на чертеже.
- Назовите точки, лежащие на прямой а (n).
- Назовите точки, не лежащие на прямой а (n).
- Назовите точки, не лежащие ни на прямой а, ни на прямой n.
- Рассказать о чертежных инструментах, необходимых на уроках геометрии.
- Физкультминутка.
- А теперь, друзья, все дружно встали,
- Быстро руки вверх подняли,
- В стороны, вперёд, назад.
- Повернулись вправо, влево,
- Ещё руки вверх подняли,
- В стороны, вперёд, назад.
- Повернулись вправо, влево,
- Тихо сели, вновь за дело!
- Рассмотрение геометрических иллюзий (слайды № 12, 13, 14).
В результате рассмотрения иллюзий сделать вывод о том, что нельзя доверять своим чувствам в геометрии. А непонятные факты нужно доказывать.
«Геометрия есть искусство правильно рассуждать на неправильном чертеже»
(Д. Пойя).
- Решение занимательных задач (слайды № 15, 16).
№ 1. Сколько квадратов вы видите на рисунках?
№ 2. Сколько треугольников на рисунках?
Задачи дети решают сами, предлагают варианты ответов, потом они обсуждаются и решение просматривается на слайде. При решении последней задачи на слайде
№ 16, названия треугольников можно записать в тетрадь.
9. Подведение итогов урока.