Задачи на признаки равенства треугольников (7 класс)
Задачи на тему Признаки равенства треугольников
1.
Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м
2.
Через середину О отрезка АВ проведена прямая, перпендикулярная прямой АВ. Докажите, что каждая точка Х этой прямой одинаково удалена от точек А и В
3.
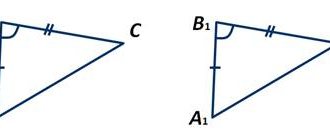
На стороне АВ треугольника АВС взята точка D, а на стороне А1В1 треугольника А1В1С1 взята точка D1. Известно, что треугольники АDC и A1D1C1 равны и отрезки DB и D1B1 равны. Докажите равенство треугольников ABC и A1B1C1
4.
Чтобы измерить на местности расстояние между двумя точками А и В, между которыми нельзя пройти по прямой, выбирают такую точку С, из которой можно пройти и к точке А, и к точке В и из которой видны обе эти точки. Измеряют расстояния АС и ВС, продолжают их за точку С и отмеряют CD = AC и ЕС = СВ. Тогда отрезок ED равен искомому расстоянию. Объясните почему
5.
Отрезки АВ и CD пересекаются в точке О. Докажите равенство треугольников АСО и DBO, если известно, что угол АСО равен углу DBO и ВО = СО
6.
Отрезки АС и BD пересекаются в точке О. Докажите равенство треугольников ВАО и DCO, если известно, что угол ВАО равен углу DCO и АО = СО
7.
Докажите равенство треугольников по медиане и углам, на которые медиана разбивает угол треугольника
9.
Периметр равнобедренного треугольника равен 1 м, а основание равно 0,4 м. Найдите длину боковой стороны
10.
Периметр равнобедренного треугольника равен 7,5 м, а боковая сторона равна 2 м. Найдите основание
11.
Периметр равнобедренного треугольника равен 15,6 м. Найдите его стороны, если основание: 1) меньше боковой стороны на 3 м; 2) больше боковой стороны на 3 м
12.
Докажите, что у равностороннего треугольника все углы равны
13.
От вершины С равнобедренного треугольника АВС с основанием АВ отложены равные отрезки: СА1 на стороне СА и СВ1 на стороне СВ. Докажите равенство треугольников 1) САВ1 и СВА1; 2) АВВ1 и ВАА1
14.
На основании АВ равнобедренного треугольника АВС даны точки А1 и В1. Известно, что АВ1 = ВА1. Докажите, что треугольники АВ1С и ВА1С равны
15.
Треугольники АСС1 и ВСС1 равны. Их вершины А и В лежат по разные стороны от прямой СС1. Докажите, что треугольники АВС и АВС1 равнобедренные
16.
Сформулируйте и докажите теорему, обратную утверждению задачи № 12
17.
На сторонах АС и ВС треугольника АВС взяты точки С1 и С2. Докажите, что треугольник АВС равнобедренный, если треугольники АВС1 и ВАС2 равны
18.
1) Докажите, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника. 2) Докажите, что середины сторон равностороннего треугольника являются также вершинами равностороннего треугольника
20.
Докажите, что у равнобедренного треугольника: 1) биссектрисы, проведенные из вершин при основании, равны; 2) медианы, проведенные из тех же вершин, тоже равны
21.
Докажите, что у равных треугольников АВС и А1В1С1: 1) медианы, проведенные из вершин А и А1, равны; 2) биссектрисы, проведенные из вершин А и А1, равны
22.
Точки А, С, В, D лежат на одной прямой, причем отрезки АВ и CD имеют общую середину. Докажите, что если треугольник АВЕ равнобедренный с основанием АВ, то треугольник CDE тоже равнобедренный с основанием CD
23.
Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу
24.
В равнобедренном треугольнике ABC с основанием АС проведена медиана ВМ. На ней взята точка D. Докажите равенство треугольников: 1) ABD и CBD; 2) AMD и CMD
25.
Докажите, что треугольник ABC равнобедренный, если у него 1) медиана BD является высотой; 2) высота BD является биссектрисой; 3) биссектриса BD является медианой
26.
Даны два равнобедренных треугольника с общим основанием. Докажите, что их медианы, проведенные к основанию, лежат на одной прямой
27.
В равнобедренном треугольнике АВС с основанием ACпроведена медиана BD. Найдите ее длину, если периметр треугольника АВС равен 50 м, а треугольника ABD 40 м
28.
Докажите, что биссектриса равнобедренного треугольника, проведенная из вершины, противолежащей основанию, является медианой и высотой
29.
У треугольников ABC и A1B1C1 AB = A1B1, AC = A1C1, C = C1 = 90(прямоугольные). Докажите, что ΔABC = ΔA1B1C1
30.
Докажите, что у равнобедренного треугольника высота а, опущенная на основание, является медианой и биссектрисой
31.
Треугольники АВС и АВС1 равнобедренные с общим основанием АВ. Докажите равенство треугольников АСС1 и ВСС1
32.
Точки А, В, С, D лежат на одной прямой. Докажите, что если треугольники АВЕ1 и АВЕ2 равны, то треугольники CDE1 и CDE2 тоже равны
33.
Два отрезка АВ и CD пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников ACD и BDC
34.
Докажите равенство треугольников по двум сторонам и медиане, проведенной к одной из них
35.
Отрезки АВ и CD пересекаются. Докажите, что если отрезки АС, СВ, BD и AD равны, то луч АВ является биссектрисой угла CAD и луч CD биссектрисой угла АСВ
36.
Докажите, что в задаче № 35 прямые АВ и CD перпендикулярны
37.
Треугольники АВС и BAD равны, причем точки С и D лежат по разные стороны от прямой АВ. Докажите, что 1) треугольники CBD и DAC равны; 2) прямая CD делит отрезок АВ пополам
38.
Отрезки равной длины АВ и CD пересекаются в точке О так, что АО = OD. Докажите равенство треугольников АВС и DCB
39.
Докажите равенство треугольников по двум сторонам и медиане, исходящим из одной вершины
40.
Докажите равенство треугольников по стороне, медиане, проведенной к этой стороне, и углам, которые образует с ней медиана
.
Решение задач на применение признаков равенства треугольников
1) Автор: Козлова Татьяна Геннадьевна
2) 2 квалификационная категория
3) п. Пристанционный Тоцкого района Оренбургской области
4) МБОУ Пристанционная основная общеобразовательная школа
5) дисциплина: геометрия
6) учебник: Л.С. Атанасян и др. Геометрия 7-9
7) урок Решение задач на применение признаков равенства треугольников
 7 класс
7 класс
9) продолжительность урока: 45 минут Используемая литература:
1. Атанасян Л.С., Бутузова В.Ф. и др. учебник Геометрия 7-9.- М.: Просвещение, 2005
2. Гаврилова Н.Ф. Поурочные разработки по геометрии. 7 класс — 2-е издание — М.: ВАКО, 2006
3. Панарина В.И. Геометрия. Диагностические тесты. 7 класс.- М.: Национальное образование, 2012
4. Мищенко Т.М. Рабочая тетрадь по геометрии. — М.: Астрель, 2012 Решение задач на применение признаков равенства треугольников
Тема
: решение задач на применение признаков равенства треугольников
Цель
: развитие умения учащихся применять признаки равенства треугольников при решении геометрических задач;
Задачи
:
обучающая:
· повторить и систематизировать знания учащихся по теме «Признаки равенства треугольников»
· развивать умение учащихся оформлять решение геометрических задач, вести доказательство, строить цепочку логических рассуждений, ведущих к решению задачи;
развивающая:
· развививать внимание, логическое мышление, математическую речь учащихся;
воспитывающая:
· воспитывать у учащихся уважительное отношение к мнению окружающих, развивать самостоятельность школьников.
Тип урока
: урок комплексного применения знаний, умений, навыков учащихся
Форма урока
: традиционный
Оборудование
: доска, тетрадь, учебник, карточки(приложение 1, приложение 2, приложение 3).
План урока
:
1. Организационный момент (3 мин.)
2. Актуализация знаний (10 мин.)
3. Решение задач (20 мин.)
4. Домашнее задание (2 мин.)
5. Проверочная работа (10 мин.)
6. Итог (1 мин) Ход урока
I. Организационный момент
Приветствие учителем учащихся. Ознакомление учащихся с планом урока. II. Актуализация знаний
Индивидуально у доски
3 человека готовят доказательство:
а) первого признака равенства треугольников (первый человек);
б) второго признака равенства треугольников (второй человек);
в) третьего признака равенства треугольников (третий человек). Со всем классом (устно)
: решение заданий карточки (Приложение 1). 1. Укажите номера верных утверждений:
1) Геометрия — это наука, в которой изучаются фигуры на плоскости.
2) Две не совпавшие прямые могут иметь только одну общую точку.
3) Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками.
4) Если точка С лежит на отрезке АВ, то длина отрезка АС равна сумме длин АВ и ВС.
5) Длину отрезка можно измерить линейкой.
6) Отрезок не является геометрической фигурой. 2. Решите задачи:
1) На отрезке FNотмечена точка Q. Известно, что FQв 2 раза больше QN. Какова длина отрезка FQ, если FNравна 240 см? Ответ дайте в дециметрах.
2) Луч ВМ проходит между сторонами угла АВС. Известно, что угол АВМ на 30меньше угла МВС. Какова градусная мера угла МВС, если угол АВС равен 150? Заслушивание доказательств
III. Решение задач
1. Решение задач по готовым чертежам (письменно в тетради с комментированием с места) — (Приложение 2):
Задача 1
Дано:
АВ=АС, угол АСFравен углуАBD
Доказать: равенство углов ACF и ABD
Наводящие вопросы:
1. Что необходимо доказать? (равенство углов ACF и
ABD
)
2. На что опираемся при решении геометрических задач? (на определения и теоремы)
3. Какие теоремы нам помогут доказать равенство треугольников? (учащиеся формулируют признаки равенства треугольников)
Перечислите равные элементы у данных треугольников.( АВ=АС, угол АСF равен углу АBD— по условию)
4. Сколько равенств получилось? (два)
5. Найдите еще по 1 равному элементу у данных треугольников. (угол А — общий)
6. Запишите решение задачи.
Решение
:
АВ=АС (по условию), угол АСF равен углу АBD(по условию), угол А — общий угол ACF равен углу ABD (по 2 признаку равенства треугольников). Что и требовалось доказать.
Задача 2
Дано: АF= 15 см, FС = 10 см, АС = 7 см.(рис.1)
Найти стороны треугольника АВD.
Решение
В задаче 1 доказали, что треугольник ACFравен треугольнику ABD. Из равенства треугольников следует равенство соответствующих сторон, следовательно АF= AD= 15 см, FС = BD= 10 см, АС = АВ = 7 см.
Задача 3
Дано: АО = ОС, угол ВАО равен углу DCO. (рисунок 2)
Доказать: АВ = СD
Наводящие вопросы
:
1.
Из чего может следовать равенство сторон треугольников?
(из равенства данных треугольников)2.
Укажите равные элементы данных треугольников.
(АО = ОС, уголВАО равен углуDCO)3.
Какой из признаков равенства треугольников нам может пригодиться? (первый или второй)
4.
Запишите решение задачи.
Решение
АО = ОС, угол ВАО = углу DCO(по условию), угол АОВ = угол СOD(так как углы вертикальные). Тогда по второму признаку равенства треугольников ВАО и DCO. Следовательно, АВ = СD.
Задача 4
Дано: АВ = DC АD= ВС PABC= 15 см PABCD=20 см (рисунок 3) Найти: АС
Решение:
1. PABCD=20 см, PABCD= АВ + ВС + CD+ AD. Обозначим АВ = х, ВС = y, тогда PABCD= АВ + ВС + CD+ AD= 2(х+y). Отсюда х + y= 10.
2. PABC= 15 см. PABC= АВ + ВС + СА. Отсюда СА = 15 — 10 = 5 (см) Ответ
: 5 см.
Задача 5
Дано: АВ = ВС AD = DC угол ABD = 63 угол ADB = 37 (рисунок 4) Найти: угол CBD, угол CDB.
Решение:
1. Так как АВ = ВС (по условию), AD= DC(по условию), BD— общая сторона, то треугольник АВD равен треугольнику СBD 2. угол CBD равен углу ABD и равен 63, угол CDB равен углу ADB и равен 37
Ответ
: угол CBD = 63, угол CDB = 37
2. Работа с учебником
№ 158
Наводящие вопросы
· Прочитайте задачу · С чего начинается решение геометрических задач? (с построения чертежа) · Какая фигура дана? (равнобедренный треугольник) · Какой треугольник называется равнобедренным? · Какие теоремы вам известны про равнобедренный треугольник? · Постройте чертеж равнобедренного треугольника. · Что известно про данный треугольник? · Что называется медианой треугольника? · Как отметить медиану треугольника на чертеже? · Отметьте медиану АD. · Что известно про периметры? · Что необходимо найти? Дано:
АВС — равнобедренный АС — основание АС = 8 см АD— медиана а) РАВD> PADCна 2 см б) РАВD< PADCна 2 см
Найти: АВ
Решение.
1. Пусть BD= xсм, значит и DC= х см, так как AD — медиана. Следовательно, ВС = АВ = 2х см, так как трегольник АВС равнобедренный.
2. Обозначим АD за у. 1 случай: РАВD= 2х + х + y, а периметр треугольника ADC равен 8+х+y. Найдем разницу между значениями периметра ABD и периметра ADC: 2=2х-8. Решив полученное уравнение, найдем х=5. 5 см — длина BD, тогда АВ = 10 см.
2 случай: Если периметр треугольника ADC больше периметра треугольника ABD на 2 см, тогда вычтем из большего значения меньшее. В результате получим уравнение: 2=-2х+8. Решив данное уравнеие, найдем значение х, равное 3. , то есть 3 см — длина BD, тогда АВ = 6 см Ответ: 6 см или 10 см.
IV. Домашнее задание
№ 157, № 162(б) V. Проверочная работа
(Приложение 3) 1. Укажите номера чертежей, на которых изображены равные треугольники, в скобках запишите равенство треугольников и укажите номер признака равенства треугольников, на который вы опирались, делая вывод. 2. Отрезок DA— медиана равнобедренного треугольника BDC, проведенная к основанию СВ. Найдите углы треугольника АDC, если угол BDCравен 120, угол DBC— 30.
VI. Итог
· какие теоремы мы использовали на уроке? · зачем нужны теоремы?
Геометрия 7 класс объяснение основных тем, понятно для детей
первые геометрические объекты
Начать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.
Первыми геометрическими фигурами, которые стоит усвоить, являются точка, прямая, отрезок.
Точка — это абстрактный объект в пространстве. Никаких измерительных характеристик она не имеет (но можно определить координаты).
Через две точки можно провести прямую линию (причем единственную); она не искривляется, не имеет конца и начала, продолжается до бесконечности.
Иными словами, прямая — это множество точек на одной линии, продолжающееся до бесконечности.
Запомните важную аксиому:
Если часть прямой линии ограничить точками, получится отрезок. У отрезка есть и начало, и конец. Обозначается он большими буквами (например, отрезок КL, SD, AB и т.д.).
Если две прямые пересекаются под углом 90º, то говорят, что они перпендикулярны.
Если прямую ограничить только одной точкой, то получится два луча. У луча есть начало, а конца нет (уходит в бесконечность). Называют луч двумя буквами, например, ОА.
Еще одна фигура — угол. Он представляет собой точку и два луча, исходящие из нее. Лучи — это стороны угла, а начало этих сторон — его вершина. От того, сколько градусов составляет угол, зависит тип треугольника, который можно образовать.
О равных треугольниках. Равнобедренный треугольник
Треугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.
Сумма всех углов в треугольнике равняется 180º. Знание этого факта пригодится при решении задач на нахождение углов.
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.
Если один треугольник (назовем его CFD) наложить на другой (C1F1D1) и они будут соответствовать друг другу, то треугольники равны. У равных фигур все элементы равны.
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.
Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.
На заметку! Если равны все стороны, а не только две, то треугольник уже равносторонний, а не равнобедренный.
Исходя из этого, можно выделить признаки равнобедренного треугольника. Треугольник равнобедренный, если:
- 2 угла в нем равны;
- биссектриса одновременно является высотой и медианой;
- медиана — биссектриса и высота;
- высота, соответственно — медиана и биссектриса.
Если взять треугольник неравнобедренный, то эти три составляющие (высота, биссектриса и медиана) не будут совпадать (это четко прослеживается на рисунке ниже).
параллельные прямые
Если на тетрадном листе кажется, что прямые параллельны, но имеется небольшой уклон, то вполне вероятно, что за пределами листа (ведь они бесконечны), прямые пересекутся.
Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.
Показать параллельность прямых а и б можно так: а ΙΙ б.
прямоугольный треугольник и его свойства
Прямоугольным называют треугольник, в котором один из углов равен 90º. Рассмотрим название сторон такой фигуры.
Геометрические задачи на доказательство. Признаки равенства треугольников.
Все задачи взяты из книги “ОГЭ 2020. Математика. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко”
Задача 1. Два отрезка и пересекаются в точке О, которая является серединой каждого из них. Докажите равенство треугольников и .
К задаче 1
Рассмотрим треугольники COB и AOD. Они имеют равные стороны: CO=OD, AO=OB – по условию. Угол COB равен углу AOD (вертикальные). Таким образом, треугольники COB и AOD равны по первому признаку. Тогда CB=AD.
Рассмотрим треугольники COA и BOD. Они имеют равные стороны: CO=OD, AO=OB – по условию. Угол COA равен углу BOD (вертикальные). Таким образом, треугольники COA и BOD равны по первому признаку. Тогда CA=BD.
Треугольники ACD и BDC имеют общую сторону – CD. Таким образом, они равны по третьему признаку, ч.т.д.
Задача 2. Лучи и пересекаются в точке О, угол 1 равен углу 2, . Докажите, что .
К задаче 2
Чтобы доказать, что ОА=ОВ, потребуется доказать равенство треугольников AOC и OBD. В этих треугольниках мы имеем один равный элемент: нам дано, что OC=OD. Также известно, что угол 1 равен углу 2. Тогда угол , а угол , а это значит, что угол . Добавим к этому еще равенство углов AOC и BOD – они вертикальные. Таким образом, имеем равную сторону и два равных прилегающих к ней угла – а это второй признак равенства треугольников. Раз треугольники равны, то равны и их элементы: OA=OB, ч.т.д. Задача 3. В треугольнике ABC и угол 1 равен углу 2. Докажите, что угол 3 равен углу 4.
К задаче 3
Рассмотрим треугольник АВС. Нам дано, что он равнобедренный. А это значит, что углы при его основании равны: угол C равен углу В. Тогда треугольники CDA и ABE равны по второму признаку: угол 1 равен углу 2 по условию, CA=AB. Тогда в этих треугольниках равны соответствующие элементы: DA=AE. Это значит, что, в свою очередь, треугольник DEA тоже равнобедренный. А это означает, что углы при его основании равны, т.е. угол 3 равен углу 4, ч.т.д.
Задача 4. На рисунке и . Докажите, что .
К задаче 4
Равенство BD и CE можно доказать, если удастся доказать равенство треугольников ABD и AEC.
Поскольку и , то . Угол A у данных треугольников общий, таким образом, они равны по первому признаку. А это означает, что , ч.т.д.
Задача 5. Докажите, что у равных треугольников и медианы, проведенные из вершин и , равны.
Так как , то , то есть , а еще из равенства треугольников следует, что . Так как треугольники и равны по условию, то равны и углы: угол равен углу . Но тогда у треугольников и равны углы и прилегающие стороны, они равны по первому признаку. Тогда , ч.т.д.
К задаче 5